Виды масштабов. Точность масштабов.

Степень уменьшения изображения на планах и картах контуров местности называют масштабом или отношение длины линии на плане, карте к длине горизонтального проложения соответствующей линии на местности. L-длина линии на местности, а l- длина этой линии на плане, то масштаб определяется M=l/L. Масштаб, выражаемый простой дробью с единицей в числителе 1:N (1:500) называют численным.Знаменатель дроби – число, показывающее во сколько раз уменьшены предметы при изображении их на топографических планах или картах, профилях и строительных чертежах. Измерив длину линии на плане можно определить длину горизонтального проложения на местности.

1:10000, длина отрезка l=15 мм, то в натуре он равен L=l*N=15*10000=150 м.

Поэтому отрезок в натуре, соответствующий 0.1 мм на плане называют точностью масштаба.

Численный масштаб можно выразить в виде линейного масштаба. Он представляет собой прямую линию, разделённую на равные отрезки, называемые основанием масштаба. Этот отрезок соответствует определённому числу метров горизонтального проложения в натуре. Основание принимают 2 см. Левое основание делят на 10 равных частей. Точность линейного масштаба +- 0,5 мм.

Для измерения длин линий на топографических материалах (с точностью масштаба) пользуются поперечным масштабом. Для его построения на прямой откладывают основния масштаба, из концов которых выставляют перпендикуляры; левое верхнее и нижние основания делят на 10 равных частей и соответствующие точки соединяют прямыми. Наименьшее деление поперечного масштаба равно сотой доле основания. По масштабу с основанием 10 мм можно определить длины отрезков с точностью 0,1 мм.

6

Планы и карты. Условные знаки планов и карт.

Планом называется уменьшенные и подобные изображения небольших участков земной поверхности, без учёта кривизны земли. Картой называется уменьшенные и подобные изображения значительных территорий с учётом кривизны земли.Ситуация-совокупность предметов элементов и контуров местности. Рельеф- совокупность неровностей земной поверхности. Условные знаки- графические обозначения предметов местности.

Площадные условные знаки: применяются для заполнения контуров природных, сельскохозяйственных угодий; они состоят из знака границ угодий- точечный пунктир или тонкая сплошная линия -и заполняющих его изображение или условной окраски.

Линейные условные знаки: показывают объекты линейного характера (дороги, реки, линии связи), длина которых выражается в данном масштабе. У знаков приводятся различные характеристики объектов.

Внемасштабные условные знаки: служат для изображения объектов, размеры которых не выражаются в масштабе карты (мосты, колодцы, геодезические пункты). У них определяют местоположение объектов.

Пояснительные условные знаки: представляют собой подписи, дающие характеристики и названия объектов. Например глубину и скорость течения рек и др.

Специальные условные знаки: устанавливают соответствующие ведомства отраслей народного хозяйства; их применяют для составления специальных карт и планов этой отрасли. Например знаки для маркшейдерских планов нефтегазовых месторождений.

Влияние кривизны Земли на результаты горизонтальных и вертикальных измерений.

Для обработки результатов геодезических измерений и при получении топографических материалов (крупно­масштабного изображения на бумаге физической поверх­ности Земли) ее точки предварительно проецируют (отно­сят) отвесными линиями на поверхность более простую, чем земная. Такой поверхностью относимости могут быть поверхности референц-эллипсоида, шара, плоскости. Проецирование точек линиями, перпендикулярными к по­верхности относимости называют ортогональным.

Получить ортогональную проекцию земной поверх­ности на плоскость наиболее просто, поскольку при этом не нужно учитывать кривизну Земли.

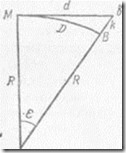
Примем Землю за шар радиуса R (рис. 8). Сравним длину дуги MB = D с длиной касательной Mb = d. Получим d = R tgепсилонд и D = Rепсилонд. Обозначим разность (d — D) через дельтаd, тогда дельтаd = R(tg e — e).

Ограничимся первыми двумя членами этого убывающего ряда и пренебрежём последующими из-за их малости, тогда дельтаd=Re^3/3=d^3/3R^2

При R =15000 км и d = 10 км, получим

Дельтаd/d=1/3*36*10^4=1/1000000

7

Такой погрешностью характеризуются наиболее точные геодезические измере­ния. Следовательно, участки земной по­верхности размером 20x20 км² во всех случаях можно считать плоскими.

Рис. 8. Влияние кривизны Земли на точность определе­ния высот

Определим величину выражающую влияние кри­визны Земли на точность определения высот точек земной У поверхности.

Из прямоугольного треугольника О Mb

d²=(R + k)^2 — R^2 = 2Rk + k^2; откуда k =d²/{2R + k).

Поскольку величина k мала по сравнению с радиусом R Земли, то k = d²/2R

Придавая d различные значения, получим следующие значения k:

d, м.................. 100 300 500 1000

k, см.................. 0,1 0,8 2,1 8,3

При возведении строительных конструкций погреш­ности высотных измерений и построений в среднем не должны превышать 1-2 мм, поэтому влияние кривизны земли на определение высот должно учитываться.