18.5. Закон Бойля-Мариотта

Традиционный эксперимент Бойля-Мариотта дает превосходную воз­можность обсудить идеи, представленные выше. Система, стенки и окруже­ние идентифицированы с воздухом в трубке, стеклянными стенками трубки и атмосферой соответственно. Удобными термодинамическими координатами являются давление p и объем V воздуха, которые нанесены на график рис. 18.12. Когда трубка с ртутью регулируется, чтобы изменить объем, необходимо выждать некоторое время, пока уровни не установятся, перед снятием пока­заний, что система достигла тепловое равновесие с окружением.

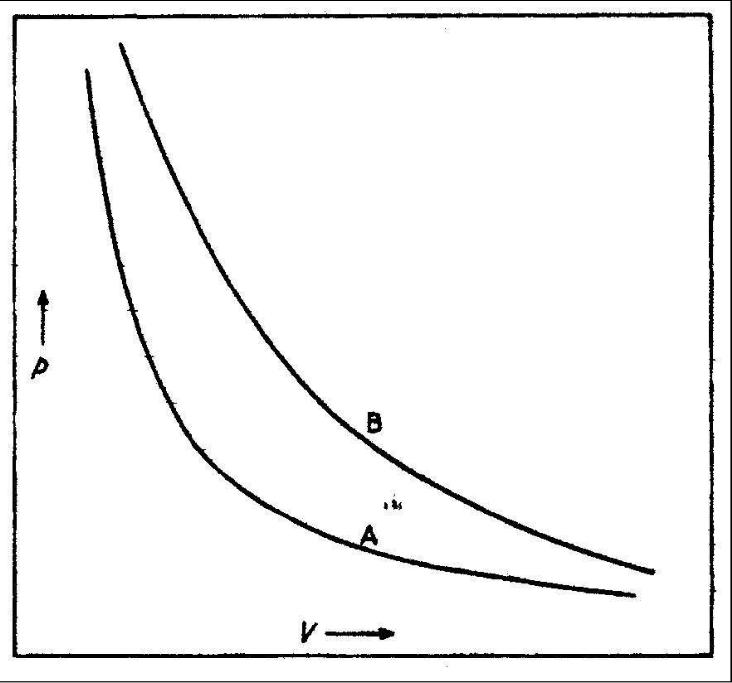
Рис. 18.12. Изотермы p − V для газа.

Следовательно, если термодинамическое состояние окружения оста­ется постоянным в течение эксперимента (что контролируется, например, не­градуированным стеклянным ртутным термометром), точки на графике пред­ставляют состояния, которые, согласно нулевому закону находятся в тепло­вом равновесии друг с другом. Такой процесс называется изотермическим и очевидно происходит при постоянной температуре. Линия, проведенная через эти точки на графике, показывает зависимость между двумя термодинамиче­скими координатами - давлением и объемом при изотермических условиях и называется изотермой. Когда мы примем процедуру для того, чтобы припи­сывать числовые значения температуре, мы будем маркировать изотерму со­ответствующей температурой.

График log(p) от log(V ) является прямой линией с наклоном -1 прибли­зительно, что соответствует уравнению pV = const для изотермических процессов в газе. Это и есть закон Бойля-Мари­отта.

Детальные исследования в широких диапазонах давлений показывают, что газы описываются законом Бойля-Мариотта довольно хорошо при низ­ких давлениях, в то время как есть значительные отклонения от этого закона в области высоких давлений, особенно вблизи перехода в сжиженное состоя­ние. Это и приводит к понятию идеального газа как газа, который описыва­ется законом Бойля-Мариотта во всем диапазоне давлений и температур.

Значение произведения pV в изотермическом процессе может быть свя­зано с физиологическим ощущением тепла. Если мы повторим вышеупомя­нутый эксперимент с трубкой в паровой бане, мы получаем другую изотерму B, которая пройдет всюду выше изотермы А на рис. 18.12.

Таким образом, произведение pV больше для горячей системы, чем для холодной. Выбирая различные параметры одного и того же вещества или одинаковые параметры различных веществ, можно установить множество температурных шкал. Но даже в том случае, когда численные значения тем­пературы двух или большего числа постоянных точек на этих шкалах будут по нашему выбору выражаться одними и теми же числами, нет оснований ожидать, что шкалы совпадут при других температурах. Нет также никаких оснований предпочесть из множества шкал такого типа какую-либо одну и считать ее основной. Но, очевидно, наличие множества температурных шкал вызвало бы очень большие неудобства и было бы неудовлетворительным во многих отношениях.

Результат этого эксперимента показывает, что температура зависит от термометрических свойств рабочего тела. Эксперименты показали согласие между газовыми термометрами постоянного давления и постоянного объема, но большие различия с другими термометрами. Дальнейшие исследования показывают, что есть хорошее согласие между газовыми термометрами, ис­пользующими различные газы и что это согласие улучшается при низких давлениях. Это позволяет использовать произведение pV идеального газа как величину пропорциональную температуре.

Измерение термодинамической температуры должно быть выполнено с газом при таких условиями, что его поведения близко к поведению идеаль­ного газа. Пусть мы выбрали термометр постоянного объема, содержащий реальный газ, например азот. Предположим, что давление азота, скорректи­рованное на расширение сосуда и т.д равно p_tp, когда тепловое равновесие было достигнуто между термометром и ячейкой тройной точки. Затем сосуд помещается в тепловой контакт с системой, температура которой должна быть измерена, и фиксируется равновесное давление p.

Температура T_p рассчитывается по уравнению

К (18.1)

Заметьте, что уравнение получено из уравнения 1, при условии V = V_tp. Нижний индекс p используется, чтобы указать, что температура была рассчи­тана из измерений давления реального газа. Вышеупомянутая процедура по­вторяется с меньшим количеством азота в сосуде так, чтобы и p и p_tp были меньше, и рассчитывается второе значение T_p. Дальнейшее уменьшение ко­личества азота и повторение процедуры приводят к ряду значений T_p при бо­лее низких давлениях. Полученную зависимость можно экстраполироваться, как показано на рис. 18.13, и получить значение, соответствующее нулевому давлению:

(18.2)

В предыдущих разделах мы заметили, что реальные газы удовлетво­ряют условиям закона Бойля-Мариотта при низких давлениях. Таким обра­зом, мы должны ожидать, что реальный газ удовлетворит условиям закона Бойля-Мариотта точно в пределе нулевого давления. Значение T, полученное из уравнения (18.2) соответствует поведению идеального газа и соответствует термодинамической температуре. Заметьте, что то же самое значение T было бы получено, даже в случае различных газов, используемых в термометре (см. рис. 18.13).

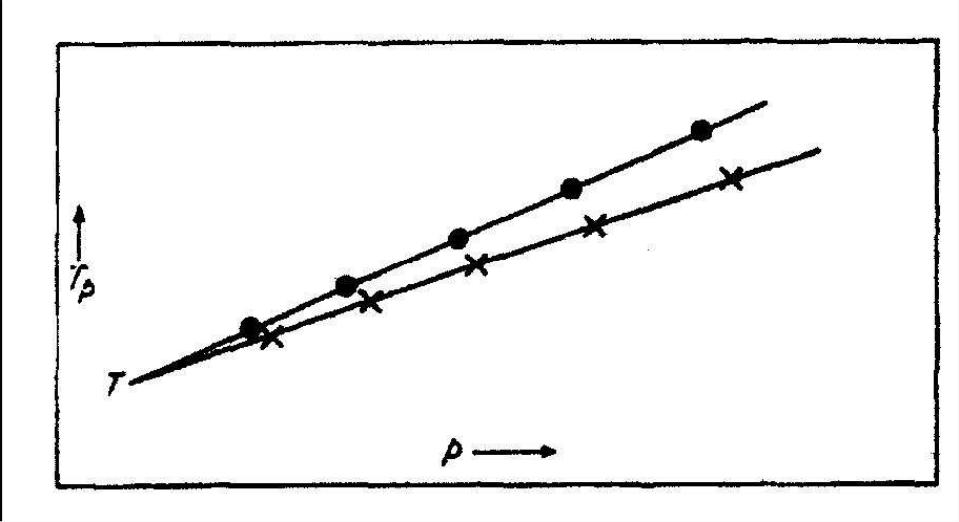
Рис. 18.13. Экстраполяция вычисленных значений T_p при p 0 для двух разных газов.

Длинная, утомительная процедура, описанная выше является очевидно неподходящей для большинства температурных измерений. Однако, она ис­пользуется, чтобы определить температуры равновесных состояний кипяче­ния и температуры замерзания некоторых веществ.

Определение температуры в терминах поведения идеального газа имеет то преимущество, что она не зависит от свойств рабочего тела. Можно пока­зать, что температура идеального газа идентична температуре в термодина­мической шкале, предложенной в 1848 Томсоном (лорд Кельвин), если ис­пользуется та же самая фиксированная точка. Термодинамическая темпера­тура базируется на действии идеальной тепловой машины и независима от свойств рабочего тела.