18.4. Тепловое равновесие и температура

Рассмотрим, как было достигнуто современное определение темпера­туры и как тесно это связано с понятием идеального газа. Сделаем это на ос­нове макроскопических наблюдений, без каких-либо предположений о внут­ренней структуре вещества.

В термодинамике область пространства или количество вещества, ко­торые мы изолируем мысленно или физически и на которых мы концентри­руем наше внимание, называют системой. Все вне системы, на которую мо­жет, конечно, воздействовать то, что находится снаружи, названо окруже­нием. Система отделена от окружения стенкой, сквозь которую никакие хи­мические реакции или массообмен не происходят, так что масса системы ос­тается постоянной.

Чтобы описывать поведение системы и ее взаимодействий с окруже­нием и с другими системами, мы должны определить значения некоторых величин, таких как давление, размеры и т. д. Такие величины, которых не так много и которые являются прямо наблюдаемыми, названы макроскопиче­скими координатами. (Заметьте, что слово координата используется здесь в том же самом смысле, что и на графиках.) Другой вариант, который включает предположения о внутренней структуре вещества, должен определить коор­динаты положений и скоростей (возможно и других) материальных точек, из которых состоит система, как в кинетической теории газов. Это - микроско­пические координаты; они прямо не наблюдаемы, и их чрезвычайно много - кубический сантиметр воздуха содержит приблизительно 1019 молекул.

Исследования в физике начинаются с рассмотрения макроскопических координат, которые относятся к двум группам:

- Внешние координаты, такие как смещение, скорость и импульс сис­темы в целом;

- Внутренние или термодинамические координаты, такие как давление и объем, которые позволяют нам описать внутреннее состояние системы.

Рассмотрите, например, сосуд, содержащий известную массу газа. Ки­нетическая энергия газа в целом в любой момент может быть рассчитана из наблюдений движения сосуда, но эти наблюдения не дают никакой инфор­мации о внутреннем состоянии газа. Та же самая масса газа в сосуде боль­шего объема будет вообще иметь более низкое давление, но, независимо от размера сосуда, кинетическая энергия газа будет та же самая, если скорость сосуда та же самая. В этом случае скорость и кинетическая энергия газа в це­лом - внешние координаты, в то время как его давление и объем - внутренние или термодинамические координаты. Значения термодинамических коорди­нат определяют термодинамическое состояние системы. Когда все его тер­модинамические координаты становятся постоянными, система, как говорят, достигает состояния термодинамического равновесия.

Взаимодействия, которые могут произойти между системой и ее окру­жением или между одной системой и другой определяются природой стенок. Эти взаимодействия могут классифицироваться как механическая работа, как в случае растяжения пружины, или тепловые, когда тело помещается в пламя горелки. Оба типа процесса могут привести к изменениям в термодинамиче­ских координатах системы. Мы рассматриваем случай тепловых взаимодей­ствий.

Рассмотрим две системы А и B. Пусть система А содержит некоторое количеством воздуха в емкости, а система В представляет собой медный блок, внутри которого находится катушка проволоки высокого сопротивле­ния, сквозь которую может проходить электрический ток. На рис. 18.9 система А находится в термодинамическом равновесии (ее объем и давление являются установившимся) и изолирована толстой стенкой дерева или полисти­рола от системы B, которая находится также в равновесии в отсутствии тока. Когда ток пропускается через нагреватель в системе B, таким образом изме­няя его состояние (нагревая ее), нет никакого непосредственного эффекта на систему A; только через достаточно продолжительное время возможно заме­тить изменения давления и объема. Это приводит нас к идеальному понятию, называемому адиабатической перегородкой, которая позволяет изменять со­стояния двух систем независимо друг от друга. Адиабатический процесс - процесс, который происходит в системе, термически изолированной от дру­гих систем и от окружения. Сосуд Дьюара (термос) - хорошая практическая реализация такой адиабатической оболочки.

Рис. 18.9. Системы А и В термически изолированы друг от друга адиабатической стенкой. Изменение состояния одной из систем не влияет на состояние другой.

На рис. 18.10 те же самые две системы были приведены в прямой контакт. В этом случае прохождение электрического тока через катушка в системе B заставляет изменяться давление в системе А, то есть состояние одной сис­темы влияет на состояние другой. Стенка, которая позволяет это делать на­звана диатермической мембраной. Это - общая граница систем А и B на Рис 10, но во многих практических ситуациях тонкий слой металла играет роль хорошей диатермической мембраны. Две системы, отделенные диатермиче­ской мембраной, как говорят, находятся в термическом (тепловом) контакте.

Когда системы А и B находятся в термическом контакте друг с другом, но термически изолированы от окружения их термодинамические коорди­наты становятся установившимися через некоторое время. Они находятся то­гда в тепловом равновесии друг с другом. Практически, когда мы говорим, что две системы находятся в тепловом равновесии, мы подразумеваем, что если они были приведены в термический контакт, тогда не будет никаких изменений в их наблюдаемых свойствах.

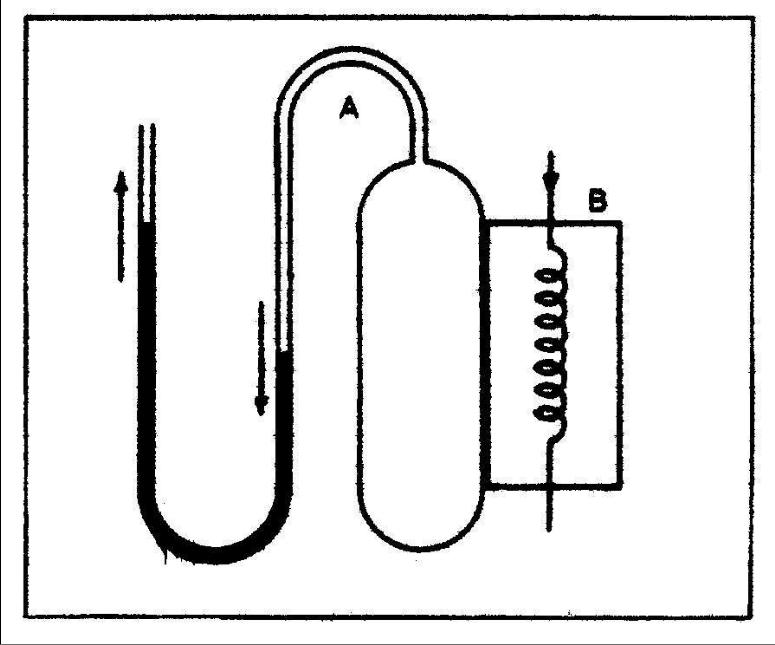
Рис. 18.10. Системы А и В находятся в тепловом контакте друг с другом через диатермическую стенку.

На рис. 18.11a представлены три системы A, B и C, изолированные от ок­ружения адиабатической перегородкой. Системы А и B изолированы друг от друга адиабатической перегородкой, но каждая из них находится в тепловом контакте с системой C через диатермическую мембрану. Каждый из систем А и B отдельно достигнет теплового равновесия с системой C. Когда адиабати­ческая перегородка между системами А и B заменяется диатермической стенкой (рис. 18.11b), никакие изменения в системах А и B не происходят. На­конец на рис. 18.11c диатермическая мембрана, отделяющая систему C от дру­гих двух систем заменена адиабатической перегородкой. Никакие изменения не происходят и в этом случае, потому что системы А и B уже находятся в тепловом контакте и в равновесии. Таким образом, мы обнаружили, что две системы, каждая из которых находится отдельно в тепловом равновесии с третьей системой, находятся и в тепловом равновесии друг с другом. Это и есть нулевой закон термодинамики и это базис понятия температуры и прин­цип температурных измерений.

Свойство, которое имеет то же самое значение для всех систем в теп­ловом равновесии, названо температурой; таким образом системы A, B и C имеют одну и ту же температуру, если две системы, имеющие различные температуры приведены в тепловой контакт, их термодинамические коорди­наты изменяются до тех пор, пока системы не достигают теплового равнове­сия друг с другом, то есть пока они оба не будут иметь одну и ту же темпера­туру.

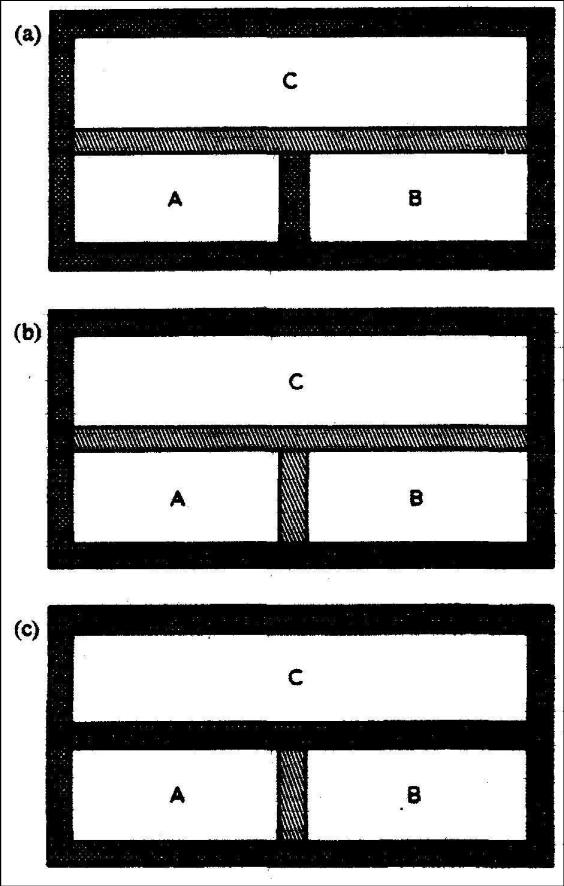
Рис. 18.11. Нулевой закон термодинамики.

Заштрихованые стенки - диатермические.

Температура измеряется термометром, который является просто систе­мой, имеющей термодинамические координаты, которые легко наблюдать. Система А на рис. 18.11 может служить таким примером. Предположим, что мы измеряем давление, когда некоторый ток течет через катушку и достигнуто тепловое равновесие между системами А и B. Допустим теперь, что система А удаляться от B и помещена в тепловой контакте с ванной с жидкостью. Если показания манометра остаются теми же самыми, что и прежде, мы мо­жет сказать, что медный блок и ванна имеют одну и ту же температуру, хотя мы еще не имеем возможности дать числовое значение температуры.