25Индексы условий внешней торговли.

К индексам, характеризующим условия внешней торговли страны относятся следующие индексы:

– общих условий торговли;

– реальных (ценовых) условий торговли;

– валовых (объёмных) условий торговли;

– покупательной способности экспорта.

Индекс общих условий торговли – это отношение индекса стоимости экспорта РФ к индексу стоимости импорта РФ

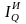
Если индекс общих условий торговли превышает 1, то это свидетельствует о более благоприятных условиях внешней торговли в отчетном периоде по сравнению с предыдущим.

Индекс реальных (ценовых) условий торговли – это отношение индекса средних цен экспорта РФ к индексу средних цен импорта РФ

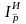
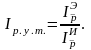
Данный индекс характеризует эффективность товарообмена страны. Он отвечает на вопрос: сколько товаров можно дополнительно импортировать в текущем периоде на сумму выручки от экспорта по сравнению с базисным периодом и, как следствие, либо расширение, либо сужение импортных возможностей страны.

Индекс валовых (объёмных) условий торговли – это отношение индекса физического объема экспорта РФ к индексу физического объема импорта РФ

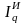
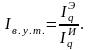
Если индекс валовых условий торговли больше 1 то это свидетельствует о том, что страна получает меньше материальных ценностей из-за рубежа на единицу экспортируемых товаров по сравнению с базисным периодом,

Индекс покупательной способности экспорта – это произведение индекса физического объёма экспорта на индекс реальных условий торговли :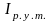

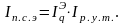
Индекс покупательной способности экспорта служит для оценки импортных возможностей страны при изменении реальных условий торговли.

26Вариационные ряды распределения в статистике внешней торговли, виды, порядок построения и графического отображения.

Ряд единиц совокупности, имеющих различные значения признака, может быть представлен в виде вариационного ряда.

Вариационный ряд – это расположение значений случайной выборки ( ) с функцией распределения F(x) в порядке их возрастания: 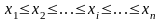, где i -й член вариационного ряда называется i -й порядковой статистикой, а номер члена вариационного ряда - рангом, порядком.

Для определения свойств вариационного ряда (в случае большого количества единиц совокупности) производится группировка и строится ряд распределения единиц совокупности по значениям изучаемого признака. Ряд распределения может быть дискретным и интервальным.

Дискретный ряд распределения представляет собой ряд конкретных значений признака x_i и соответствующих этим значения частот f_i . Число групп в дискретном ряду равно числу различных значений варьирующего признака.

Интервальный ряд распределения – это ряд, состоящий из интервалов варьирующего признака x_i и числа единиц совокупности, попадающих в данный интервал f_i – частот, или долей числа единиц совокупности в интервале в общей численности единиц совокупности w_i – частостей.

Построение ранжировонного ряда распределения

Ввиду огромного массива данных применение сплошного наблюдения экономически нецелесообразно, поэтому в таких случаях применяется выборочный метод, то есть из общего массива данных (генеральная совокупность) отбирается некоторая часть (выборочная совокупность, или выборка), которая и подвергается статистическому анализу. При этом число единиц в выборке обозначают п, во всей генеральной совокупности – N. Отношение n/N называется относительный размер или частость выборки. Качество результатов выборочного метода зависит от репре­зентативности выборки, т.е. от того, насколько она представительна в генеральной совокупности. Для обеспечения репрезентативности вы­борки необходимо соблюдать принцип случайности отбора единиц.

Предельная ошибка выборки 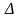= t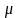

где t – коэффициент доверия, зависящий от вероятности, с которой определяется предельная ошибка выборки; – средняя ошибка выборки, определяемая для повторной выборки по формуле: = ,

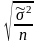для бесповторной – по формуле = ,

где n – численность выборки; N – численность генеральной совокупности.

Построение индивидуального ряда распределения

Чаще всего число групп в ряду распределения определяют по формуле Стерждесса Error: Reference source not found или Error: Reference source not found: 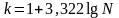3

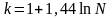4

где k – число групп (округляемое до ближайшего целого числа); N – численность совокупности.

Из формулы Стерджесса видно, что число групп – функция объема данных (N).

Зная число групп, рассчитывают длину (размах) интервала по формуле 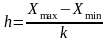(1):

(1)

где X_мax и X_min — максимальное и минимальное значения в совокупности.

Существенную помощь в анализе ряда распределения и его свойств оказывает графическое изображение. Интервальный ряд изображается столбиковой диаграммой, в которой основания столбиков, расположенные по оси абсцисс, – это интервалы значений варьирующего признака, а высоты столбиков – частоты, соответствующие масштабу по осиординат.