
- •2. Элементы линейной алгебры
- •3.Введение в математический анализ
- •4. Производная и ее приложения
- •Неопределенный и определенный интегралы
- •8. Дифференциальные уравнения
- •Кратные, криволинейные и поверхностные интегралы
- •10. Ряды
- •Теория вероятностей и математическая статистика
- •Контрольные задания
- •Оглавление
Неопределенный и определенный интегралы
201 - 210. Найти неопределенные интегралы. В пп. «а» и «б» результаты проверить дифференцированием.
201. a)
![]() esin
x
sin 2xdx; б)
arctg
x dx;
esin
x
sin 2xdx; б)
arctg
x dx;
в)
![]() ; г)
; г)
![]() ;
;
д)
![]() dx; е)
dx; е)
![]() .
.
202. a)
![]() ; б)
ex
ln(1+3ex)dx;
; б)
ex
ln(1+3ex)dx;
в)
![]() dx; г)
dx; г)
![]() ;
;
д)
![]() ; е)
(1+2cos
x)2
dx.
; е)
(1+2cos
x)2
dx.
203. a)
![]() ; б)
x
3x
dx;
; б)
x
3x
dx;
в)![]() ;
г)
;
г)![]() ;
;
д)
![]() ; е)
; е)
![]() .
.
204. a)
![]() ; б)
; б)
![]() ;
;
в)
![]() ; г)
; г)
![]() ;
;
д)
sin2
x cos2
x dx; е)
![]() .
.
205. a)
![]() ; б)
x2
e3x
dx;
; б)
x2
e3x
dx;
в)
![]() ; г)
; г)
![]() ;
;
д)
![]() dx; е)
dx; е)
![]() .
.
206. a)
![]() ; б)
; б)
![]() ;
;
в)
![]() ; г)
; г)
![]() ;
;
д)
sin
3x sin 7x dx ; е)
![]() .
.
207. a)
![]() ; б)
x
ln(x +1)dx;
; б)
x
ln(x +1)dx;
в)
![]() ; г)
; г)
![]() ;
;
д)
![]() dx;
е)
dx;
е)
![]() .
.
208. a)
![]() ; б)
x
sin
x
cos
x
dx;
; б)
x
sin
x
cos
x
dx;
в)
![]() ;
г)
;
г)
![]() ;
;
д)
x2
![]() dx; е
dx; е![]() .
.
209. a)
![]() ; б)
x2
sin 4x dx;
; б)
x2
sin 4x dx;
в)
![]() ;
г)
;
г)
![]() ;
;
д)
![]() ; е)
; е)
![]() .
.
210. a)
![]() ; б)
x
ln2
x dx;
; б)
x
ln2
x dx;
в)
![]() ;
г)
;
г)
![]() ;
;
д)
![]() ; е)
; е)
![]() .
.
211-220. Вычислить несобственный интеграл или доказать его расходимость.
211.
![]() 212.
212.
![]() .
.
213.![]() . 214.
. 214.
![]() .
.
215.
![]() . 216.
. 216.
![]() .
.
217.
![]() . 218.
. 218.
![]() .
.
219.
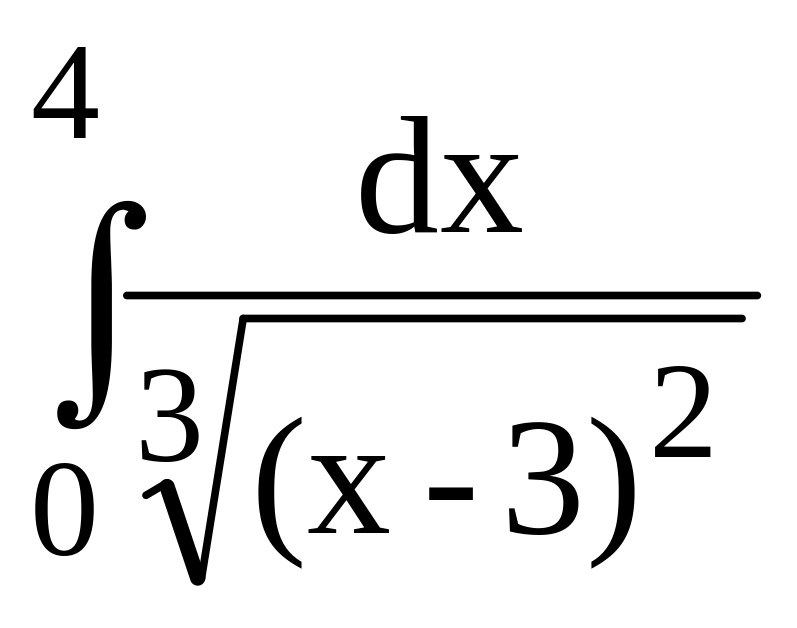 . 220.
. 220.
![]() .
.
221. Найти площадь фигуры, ограниченной параболой y = 3x2+1 и прямой y = 3x+7.
222. Найти площадь фигуры, ограниченной одной аркой циклоиды x = a(t - sin t), y = a(1- cos t) ( t ) и осью Ox.
223. Найти площадь фигуры, ограниченной кардиоидой r = 3(1+cos ).
224. Найти площадь фигуры, ограниченной четерехлепестковой розой r = 4sin 2 .
225. Вычислить объем
тела, образованного вращением вокруг
оси Ox фигуры, ограниченной параболами
y = x2
и y =
![]() .
.
226. Вычислить объем
тела, образованного вращением вокруг
оси Ox фигуры, ограниченной полуэллипсом
y = 3![]() ,
параболой x =
,
параболой x =
![]() и осью Oy.
и осью Oy.
227. Вычислить объем тела, образованного вращением вокруг Oy фигуры, ограниченной кривыми y = 2/(1+x2) и y = x2.
228. Вычислить длину
дуги полукубической параболы y =
![]() от
точки А(2; 0) до точки В(6; 8).
от
точки А(2; 0) до точки В(6; 8).
229. Вычислить длину кардиоиды r = 3(1-cos ).
230. Вычислить длину одной арки циклоиды x = 3(t - sin t), y = 3(1 - cos t) (0 t 2).
8. Дифференциальные уравнения
231 - 240. Найти общее решение дифференциального уравнения.
231. а) (x2-y2)y' = 2xy, б) 2xy' -6y = -x2.
232. а) (1+x2)y' -2xy = (1+x2)2, б) (x2-1)y' +2xy2 = 0.
233. а) xy' = y ln(y/x), б) xy' +y = y2.
234. а) xy'
+y = 3, б) y +![]() y
- xy'
= 0.
y
- xy'
= 0.
235. а) xy' +x ey/x -y = 0, б) xyy' = y2+1.
236. а) y' cos x = (y+1)sin x, б) xy' = y + x cos2(y/x).
237. а)
![]() ; б)
; б)
![]() .
.
238. а) x2y' +y = x+1, б) xy' =y ln2(y/x).
239. а) x2y' +y2-2xy = 0, б) xy' = 1+y2.
240. а) xy' +y = x+1, б) xy' = y(y-1).
241. (1-x2)y'' = xy' . 242. 2yy'' +(y')2+(y')4 = 0.
243. y'' +y' tg x = sin 2x. 244. y'' +(1/x)y' = x2.
245. 1+(y' )2+yy'' = 0. 246. (1+y)y'' -5(y')2 = 0.
247. xy''
+2![]() = x3. 248.
y''
tg y = 2(y'
)2.
= x3. 248.
y''
tg y = 2(y'
)2.
249. y'' -2y' tg x = sin x. 250. 3yy'' +(y')2 = 0.
251 - 260. Найти частное решение дифференциального уравнения y'' +py' +qy = f(x), удовлетворяющее начальным условиям y(0) = y0, y' (0)=y'0.
251. y'' +4y' -12y = 8sin 2x; y(0)=0, y' (0)=0.
252. y'' - 6y' +9y = x2-x+3; y(0)=4/3, y' (0)=1/27.
253. y'' +4y = e-2x; y(0)=0, y' (0)=0.
254. y'' -2y' +5y = xe2x; y(0)=1, y' (0)=0.
255. y'' +5y' +6y = 12cos 2x; y(0)=1, y' (0)=3.
256. y'' - 5y' +6y = (12x-7)e-x; y(0)=0, y' (0)=0.
257. y'' - 4y' +13y = 26x+5; y(0)=1, y' (0)=0.
258. y'' - 4y' =6x2+1; y(0)=2, y' (0)=3.
259. y'' -2y' +y = 16ex; y(0)=1, y' (0)=2.
260. y'' +6y' +9y = 10e-3x; y(0)=3, y' (0)=2.
261 - 270. Дана система линейных дифференциальных уравнений с постоянными коэффициентами
dx/dt = a11x+a12y,
dy/dt = a21x+a22y.
Требуется: 1) найти общее решение системы с помощью характеристического уравнения; 2) записать данную систему и ее решение в матричной форме.
261. dx/dt = 4x+6y, 262. dx/dt = -5x-4y,
dy/dt = 4x+2y. dy/dt = -2x-3y.
263. dx/dt = 3x+y, 264. dx/dt = 6x+3y,
dy/dt = 8x+y. dy/dt = -8x-5y.
265. dx/dt = -x+5y, 266. dx/dt = 3x-2y,
dy/dt = x+3y. dy/dt = 2x+8y.
267. dx/dt = -4x-6y, 268. dx/dt = -5x-8y,
dy/dt = -4x-2y. dy/dt = -3x-3y.
269. dx/dt = -x-5y, 270. dx/dt = -7x+5y,
dy/dt = -7x-3y. dy/dt = 4x-8y.
