
- •2. Элементы линейной алгебры
- •3.Введение в математический анализ
- •4. Производная и ее приложения
- •Неопределенный и определенный интегралы
- •8. Дифференциальные уравнения
- •Кратные, криволинейные и поверхностные интегралы
- •10. Ряды
- •Теория вероятностей и математическая статистика
- •Контрольные задания
- •Оглавление
4. Производная и ее приложения
121 - 130. Найти производные dy/dx данных функций.
121. a)
![]() ;
;
б) y = (ecos x + 3)2; в) y = ln sin (2x+5);
г)
![]() ; д)
tg (y/x) = 5x.
; д)
tg (y/x) = 5x.
122. а)
y =
![]() ; б)
y = (4sin x) / cos2
x;
; б)
y = (4sin x) / cos2
x;
в) y = arctg e2x ; г) y = x1/x ;
д) x-y+arctg y = 0.
123. а)
![]() ; б)
y
= 1/tg2
2x
;
; б)
y
= 1/tg2
2x
;
в) y = arcsin (1-3x) ; г) y = xln x ;
д) y sin x = cos (x-y).
124. а)
![]() ; б)
y = sin x - xcos x;
; б)
y = sin x - xcos x;
в) y = xm lnx ; г) y = x -tgx;
д) (y/x) = arctg (x/y).
125. а)
![]() ; б)
y = (sin2
x) / (2+3cos2
x) ;
; б)
y = (sin2
x) / (2+3cos2
x) ;
в) y = (x ln x)/(x-1) ; г) y = (arctg x)ln x;
д) (ex -1)(ey -1) - 1 = 0.
126. а)
![]() ; б)
y = 2tg 3(x2
+1) ;
; б)
y = 2tg 3(x2
+1) ;
в) y = 3arctg x ; г) y = (arctg x)x ;
д) y2 x = e y/x.
127. а)
![]() ; б)
y = (1/2)tg2
x+ln cos x ;
; б)
y = (1/2)tg2
x+ln cos x ;
в)
![]() ; г)
y = (x+x2)
x
;
; г)
y = (x+x2)
x
;
д) x3 +y3 - 3a xy = 0.
128. а)
![]() ;
б)
;
б)
![]() ;
;
в) y = arctg(tg2 x) ; г) y = (sinx)ln x ;
д) x-y+a sin y = 0.
129. а)
![]() ; б)
y
= 2x
e-x
;
; б)
y
= 2x
e-x
;
в) y = (arcsin x)/ 1 - x2 ; г) y = (cos x)x ;
д) ln y = arctg (x/y).
130. а)
![]() ; б)
y = (1/3) tg3
x - tg x + x;
; б)
y = (1/3) tg3
x - tg x + x;
в)
![]() ; г)
y
= (cos
x)x
;
; г)
y
= (cos
x)x
;
д) x-y+ey arctg x = 0.
131 - 140. Найти dy/dx и d2y/dx2 для заданных функций:
а), б) y = f(x); в) x = (t), y = (t).
131. а) y = x/(x2 -1); б) y = (ecos x +2)3 ;
в) x = cos (t/2), y = t - sin t.
132. а)
y = ln ctg 2x; б)
y = x
![]() ;
;
в) x = t3 + 8t, y = t5 + 2t.
133. а) y = x3 ln x ; б) y = arctg e4x ;
в) x = t - sin t, y = 1 - cos t.
134. а) y = x arctg x ; б) y = 3 cos 5x ;
в) x = e 2t ; y = cos t.
135. а) y = arctg x ; б) y = ex cos 2x;
в) x = 3cos2 t, y = 2sin3 t.
136. а) y = ectg 3x; б) y = ln cos 5x ;
в) x = 3cos t, y = 4sin2 t.
137. а) y = ex cos x; б) y = tg (x4 +5) ;
в) x = 3t-t3, y = 3t2 .
138. а) y = e-x sin x ; б) y = x ctg 8x ;
в) x = 2t-t3 , y = 2t2 .
139. а)
y = x![]() ; б)
y = (x2-2x-1)
cos 4x ;
; б)
y = (x2-2x-1)
cos 4x ;
в) x = t+ln cos t, y = t - ln sin t.
140. а) y = x e-x; б) y = e-cos x ;
в) x = ln t, y = (1/2)(t-1/t).
141 - 150. Найти наибольшее и наименьшее значения функции y=f(x) на отрезке [a;b].
141. f(x) = x3 - 12x + 7; [0; 3].
142. f(x) = x5 - (5/3)x3 + 2; [0; 2].
143. f(x) =
![]() x
+ cos x; [0; /2].
x
+ cos x; [0; /2].
144. f(x) = 3x4 - 16x3 + 2; [-3; 1].
145. f(x) = x3 - 3x + 1; [1/2; 2].
146. f(x) = x4 + 4x; [-2; 2].
147. f(x) = x - sin x; [0; /2].
148. f(x) = 81x - x4; [-1; 4].
149. f(x) = 3 - 2x2 ; [-1; 3].
f(x) = x - sin x ; [-; ].
Приложения дифференциального
исчисления
151 - 160. Исследовать методами дифференциального исчисления функцию y=f(x) и, используя полученные результаты, построить ее график.
151. y = 4x/(4+x2). 152. y = (x2-1)/(x2+1).
153. y = (x2+1)/(x2-1). 154. y = x2/(x-1).
155. y = x3/(x2+1). 156. y = (4x3+5)/x.
157. y = (x2-5)/(x-3). 158. y = x4/(x3-1).
159. y = 4x3/(x3-1). 160. y = (2-4x2)/(1-4x2).
Дифференциальное исчисление функций
нескольких переменных
161 - 170.
Найти а)
![]() ;
;
![]() ;
б)
;
б)
![]() ;
;
![]() ;
;
![]() .
.
161.a) z = cos (x/y2 ) +5x, б) u = xz/(x+y+z3 );
162. а) z = 3x2/(x+y), б) u = sin (x2+y2+2z+1);
163. а) z = arcsin(x+6y) - 2y5; б) u = cos (x/y2) +5z cos (x/z2 );
164. а) z = y/(x3-y2)2; б) u = sin (x2+y2) - ln(x2+4z4);
165. а) z = ln(x+5e-3y); б) u = arcsin(3zx+6y);
166. а) z = ln( 3xy+e-3xy ); б) u = xz eyz/x;
а) z = 5xcos(y) ; б) u = xz + ln(yx2+6z4);
168. а) z = sin(x+4y5); б) u = arccos(3z3x+6y);
169. а) z =5x2 +y2 +tg(4x/y); б) u = x [ln (z+1) - yln z];
170. а) z =5yx2 + arccos(3x3+6y); б) u = xtg(eyz/x ).
171 - 180. Дана функция z=f(x,y). Показать, что
![]() .
.
z = y/(x2-y2)5; F =
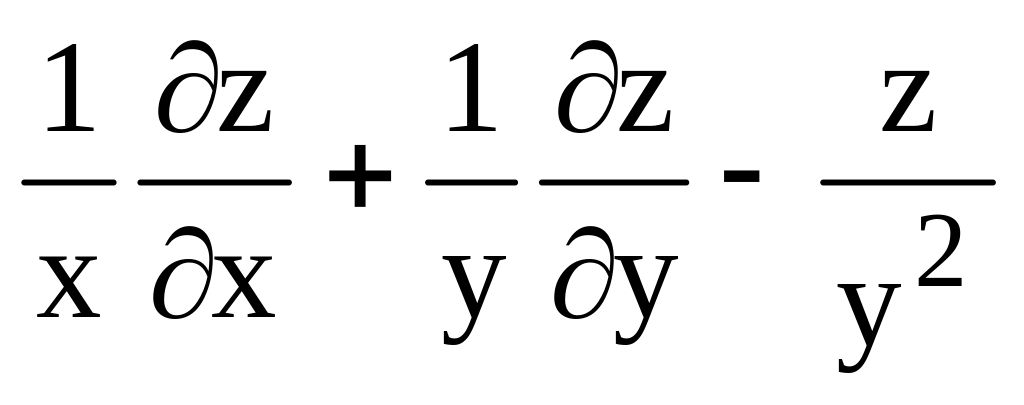 .
.
172. z =
y2/(3x)+arcsin(xy); F
=![]()
173. z =
ln(x2+y2+2x+1); F
=![]() .
.
174. z =
exy
; F =![]() .
.
175. z =
ln(x+e-y);
F =![]() .
.
176. z =
x/y; F =![]() .
.
177. z =
xy; F
=![]() .
.
178. z = x
ey/x;
F =![]() .
.
179. z =
sin(x+ay); F =![]() .
.
180. z = cos y+(y-x) sin y; F = (x-y) .
181 - 190. Найти наименьшее и наибольшее значения функции z=f(x;y) в замкнутой области D, заданной системой неравенств. Сделать чертеж.
181. z = x2+y2-9xy+27; 0x3, 0y3.
182. z = x2+2y2+1; x0, y0, x+y3.
183. z = 3-2x2-xy-y2; x1, y0, yx.
184. z = x2+3y2+x-y; x1, y-1, x+y1.
185. z = x2+2xy+2y2; -1x1, 0y2.
186. z = 5x2-3xy+y2+4; x-1, y-1, x+y1.
187. z = 10+2xy-x2; 0y4-x2 .
188. z = x2+2xy-y2-4x; x0; y0; x+y+20.
189. z = x2+xy-2; 4x2-4y0.
190. z = x2+xy; -1x1; 0y3.
191 - 200. Даны функция z=f(x;y), точка А(х0;y0) и вектор а(а1;а2). Найти: 1) grad z в точке А; 2) производную в точке А по направлению вектора а.
191. z = x2+xy+y2; A(1; 1), a(2; -1).
192. z = 2x2+3xy+y2; A(2; 1), a(3; -4).
193. z = ln(5x2+3y2); A(1; 1), a(3; 2).
194. z = ln(5x2+4y2); A(1; 1), a(2; -1).
195. z = 5x2+6xy; A(2; 1), a(1; 2).
196. z = arctg(xy2); A(2; 3), a(4; -3).
197. z = arcsin(x2/y); A(1; 2), a(5; -12).
198. z = ln(3x2+4y2); A(1; 3), a(2; -1).
199. z = 3x4+2x2y3; A(-1; 2), a(4; -3).
200. z = 3x2y2+5xy2; A(1; 1), a(2; 1).
