3. Бінарні дерева

Що одна структура даних, яка використовує для свого представлення динамічні об’єкти — це дерево. Деревом називається сукупність взаємопов’язаних елементів, один з яких називається коренем (вершиною дерева), інші елементи утворюють піддерева. Кожен елемент дерева містить певні корисні дані та вказівники на корені (вершини) піддерев. Найчастіше використовуються бінарні дерева, де кожен корінь містить два вказівники: на ліве і праве піддерево. Реалізувати дерево можна за допомогою такої структури:

struct TREE //binary tree

{

int data;

TREE *left, *right;

} var_tree, *ptr_to_tree;

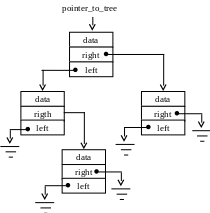
тут TREE — ідентифікатор структури типу “бінарне дерево”, var_tree — змінна типу “бінарне дерево” (вершина дерева), pointer_to_tree — вказівник на дерево (може бути порожнім — null), left — поле, що вказує на ліве піддерево (якщо null, то дана вершина не має лівого піддерева), right — поле, що вказує на праве піддерево, data — корисні дані типу SOMETYPE (наприклад, ціле число або вказівник на якийсь складніший тип даних).

О днією з основних операцій над деревами є проходження його вузлів у певному порядку. Нехай маємо дерево, у вузлах якого записані цілі числа, як показано на рисунку.

Використовуються такі способи проходження дерева: прямий (низхідний), зворотній (висхідний) та змішаний. При прямому проходженні дерева спочатку відвідують корінь, а потім у прямому порядку проходять усі його піддерева у відповідності з їхнім підпорядкуванням (ліві, а потім праві, або навпаки). Прямий прохід дерева за правилом КЛП (Корінь-Лівий-Правий) дасть послідовність чисел <15,7,23,21,50>.

При зворотньому проходженні спочатку відвідують всі його піддерева у зворотньому порядку згідно з їхньою впорядкованістю, а потім корінь. ЗА правилом ПЛК отримаємо послідовність: <50,21,23,7,15>.

При змішане проходження дерева визначається правилами ЛКП або ПКЛ, тобто спочатку проходиться одне піддерево, потім корінь, і нарешті друге піддерево.

Часто дерева використовують для представлення відсортованих наборів даних. При цьому додавання до дерева нової вершини здійснюється з використанням певного відношення порядку, наприклад “більше-менше”. Так розглянуте вище дерево цілих чисел впорядковане за правилом: всі вершини правого піддерева мають значення інформаційного поля більше, ніж значення такого ж поля у корені, а лівого — менше, ніж у корені. Якщо використати змішане проходження даного дерева за правилом ЛКП, то тримаємо послідовність <7,15,21,23,50>, яка впорядкована за зростанням, а проходження за правилом ПКЛ дає послідовність <50,23,21,15,7>, впорядковану за спаданням.

Також дерева можуть використовуватись для запису математичних виразів, що складаються з цілих чисел, змінних, знаків операцій та дужок, при цьому знак операції представляється у корені дерева, перший операнд у лівому піддереві, а другий — у правому, а дужки стають зайвими.

Для представлення дерев використовується дужкове зображення g3. Дужковим зображенням дерева B з одного вузла є запис цього вузла. Дужкове зображення дерева B з коренем w та піддеревами B₁ , B₂ записується у вигляді w(g3(B₁), g3(B₂)). Для розглянутого прикладу дужковим записом дерева буде 15(7,23(21,50).

Реалізувати роботу з деревами можна з використанням структур, вказівників та зовнішніх функцій, проте найзручніше їх зробити методами класу “бінарне дерево”. Приклад такої реалізації наведений нижче:

// файл btree.h

class BTREE //binary tree

{

int data;

BTREE *left, *right;

public:

BTREE(int, BTREE* =0, BTREE* =0);

~BTREE();

friend BTREE* add(BTREE*,int);

void print();

void printLVR();

void printRVL();

};

Клас BTREE являє собою бінарне дерево (корінь, вершину, що містить — інформаційне поле data та вказівники на ліве (left) та праве (right) піддерева). Якщо створити статичну змінну типу BTREE то отримаємо дерево, що складається з однієї вершини, вказівник на BTREE, що рівний null (не ініціалізований) являє собою порожнє дерево (в якому немає ні одного елемента). Дані класу є закритими, тому доступ до них можливий лише через методи.

Конструктор BTREE(int, BTREE* =0, BTREE* =0) створює нове дерево та ініціалізує його інформаційне поле числом цілого типу, а вказівники на ліве та праве піддерево адресами заданими у дужках. Якщо створюване дерево складається тільки з одного вузла, то присвоюються значення “за замовчуванням” (null==0). Реалізація конструктора подана нижче:

//файл btree.cpp

#include <iostream.h>

#include "btree.h"

BTREE::BTREE(int newdata,BTREE *p_left, BTREE *p_right)

// створює нове дерево, iнiцiалiзує його корiнь

// та додає лiве i праве пiддерева, як можуть бути порожнiми

{

left=p_left;

right=p_right;

data=newdata;

}

Якщо об’єкт створюється в динамічній пам’яті з допомогою операторами new, то цей конструктор викликається автоматично і крім ініціалізації забезпечує ще і виділення потрібної кількості пам’яті для зберігання data, left та right.

Враховуючи рекурсивну природу дерев, операції над ним найзручніше реалізовувати з використанням рекурсивних функцій. Так деструктор ~ BTREE() знищує об’єкт типу BTREE, звільняє зайняту ним пам’ять, а також повинен знищити всі піддерева, на які вказують вказівники left та right, якщо вони не null (тобто не порожні):

BTREE::~BTREE()

{

if (left)

delete left;

if (right)

delete right;

}

Аналогічно реалізований рекурсивний метод void print(), що виводить на екран дерево у дужковому зображенні g3.

void BTREE::print()

{

cout<<data;

if (left||right)

cout<<'(';

if (left)

left->print();

if (right)

{

cout<<',';

right->print();

}

if (left||right)

cout<<')';

}

Причому, дужки виводяться тільки тоді, коли дерево містить хоча б одне піддерево:

if (left||right),кома — коли праве піддерево не порожнє: if (right).

Методи void printLVR(); void printRVL() реалізують змішане проходження дерева відповідно за правилами ЛКП та ПКЛ і виводять через кому значення інформаційного поля вузлів:

void BTREE::printLVR()

{

if (left)

left->printLVR();

cout<<data<<',';

if (right)

right->printLVR();

}

void BTREE::printRVL()

{

if (right)

right->printRVL();

cout<<data<<',';

if (left)

left->printRVL();

}

Додавання елемента для створення впорядкованого дерева реалізоване за допомогою зовнішньої дружньої функції add(…). Ця функція зроблена зовнішньою, а не методом класу BTREE, щоб врахувати випадок порожнього дерева, яке ще не має методів, та щоб спростити логіку її роботи, використовуючи рекурсію:

BTREE* add(BTREE* root,int newdata)

{

if (!root)

root=new BTREE(newdata);

else

if (newdata<root->data)

root->left=add(root->left,newdata);

else

root->right=add(root->right,newdata);

return root;

}

Функція бере вказівник на дерево, добавляє в нього новий вузол так щоб дерево було впорядковане та повертає вказівник на модифіковане дерево.

Функція main для робити з деревами може мати такий вигляд:

//файл tstbtree.cpp

#include <iostream.h>;

#include "btree.h"

void main()

{

int i;

BTREE *p=0;

do {

cin>>i;

if (i)

p=add(p,i);

}

while (i!=0);

p->print();

cout<<"\b \n";

p->printLVR();

cout<<"\b \n";

p->printRVL();

cout<<"\b \n";

}

Програма послідовно зчитує з клавіатури числа, додає їх в упорядковане дерево поки не буде введене число “0”, потім виводить дерево у дужковому зображені та в зростаючому і спадаючому порядку. Оператор cout<<"\b \n" використовується для того, щоб витерти зайву кому у кінці рядка та перевести курсор в новий рядок.

Результати виконання програми:

15

23

7

21

50

0

15(7,23(21,50)

7,15,21,23,50

50,23,21,15,7