
- •Матрицы, определители, системы лин. Уравнений
- •1.Матрицы и операции над ними: сложение, умножение на скаляр, произведение матриц. Свойства этих операций.
- •2.Определители произвольного порядка и их свойства. Теорема о разложении определителя по элементам строки (столбца) и следствия из нее. Необходимое и достаточное условие обращения в ноль определителя.
- •Следствие 2 (фальшивое разложение определителя)
- •3.Произвольные системы линейных уравнений. Метод Гаусса. Квадратные системы с невырожденным определителем. Формулы Крамера.
- •Векторная алгебра
- •4. Векторы. Простейшие операции над ними и их свойства. Линейная комбинация и линейная зависимость системы векторов.
- •Скалярное произведение двух векторов, его свойства и вычисление его в координатах. Применение скалярного произведения в геометрии и механике.
- •Аналитическая геометрия
- •Аффинная и декартова система координат на плоскости и в пространстве.
- •Уравнения фигуры. Основные теоремы об уравнениях и о фигурах, определяемых ими. Порядок алгебраической фигуры.
Аналитическая геометрия
Аффинная и декартова система координат на плоскости и в пространстве.
Аффинная система координат (косоугольная система координат) — прямолинейная система координат в аффинном пространстве.( Аффинное пространство — служит обобщением аффинных свойств евклидова пространства. Во многом схоже с векторным пространством, но в отличие от последнего, точки в аффинном пространстве являются равноправными. В частности в аффинном пространстве нет понятия нулевой точки или начала отсчёта. В аффинном пространстве возможно вычитать друг из друга точки и получать векторы так называемого присоединенного пространства; также возможно прибавлять вектор к точке и получать другую точку, но нельзя складывать точки друг с другом.)
Декартовой обычно называют прямоугольную систему координат с одинаковыми масштабами по осям, а общей Декартовой системой координат называют аффинную систему координат.
Основные формулы аналитической геометрии: координаты вектора, определяемого парой точек; расстояние между 2 точками; формулы деления отрезка в заданном отношении; вычисление угла между векторами; площадь треугольника; объем параллелепипеда и тетраэдра.
координаты вектора: На плоскости:Если А(х1;у1),В(х2;у2),то вектор АВ(х2-х1;у2-у1). В пространстве:Если А(х1;у1;z1);В(х2;у2;z2),то вектор АВ(х2-х1;у2-у1;z2-z1).
расстояние между 2 точками: расстояние между двумя точками равно сумме квадратов разности одноимённых координат расчитать: =корень((A2-A1)^2+(B2-B1)^2)
Если x1 и y1 - координаты точки A,
а x2 и y2 - координаты точки B,
то координаты x и y точки C,
делящей отрезок AB в отношении ![]()
![]()
![]() ,
определяются по формулам
,
определяются по формулам![]()
![]()
![]()
![]()
![]()
![]()
![]()
Площадь треугольника по известным
координатам его вершин A(x1, y1), B(x2, y2), C(x3, y3)
вычисляется по формуле![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
вычисление угла между векторами![]()
объем параллелепипеда
![]()
В координатах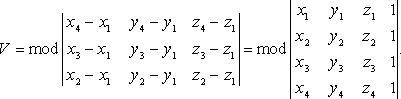
Объем тетраэдра Если ![]() -
исходящие из одной вершины ребра
тетраэдра, а
-
исходящие из одной вершины ребра
тетраэдра, а ![]() ,
, ![]() ,
, ![]() ,
, ![]() -
радиус-векторы соответствующих вершин
тетраэдра, то его объем
-
радиус-векторы соответствующих вершин
тетраэдра, то его объем
![]()
Уравнения фигуры. Основные теоремы об уравнениях и о фигурах, определяемых ими. Порядок алгебраической фигуры.
