
- •Матрицы, определители, системы лин. Уравнений
- •1.Матрицы и операции над ними: сложение, умножение на скаляр, произведение матриц. Свойства этих операций.
- •2.Определители произвольного порядка и их свойства. Теорема о разложении определителя по элементам строки (столбца) и следствия из нее. Необходимое и достаточное условие обращения в ноль определителя.
- •Следствие 2 (фальшивое разложение определителя)
- •3.Произвольные системы линейных уравнений. Метод Гаусса. Квадратные системы с невырожденным определителем. Формулы Крамера.
- •Векторная алгебра
- •4. Векторы. Простейшие операции над ними и их свойства. Линейная комбинация и линейная зависимость системы векторов.
- •Скалярное произведение двух векторов, его свойства и вычисление его в координатах. Применение скалярного произведения в геометрии и механике.
- •Аналитическая геометрия
- •Аффинная и декартова система координат на плоскости и в пространстве.
- •Уравнения фигуры. Основные теоремы об уравнениях и о фигурах, определяемых ими. Порядок алгебраической фигуры.
Векторная алгебра
4. Векторы. Простейшие операции над ними и их свойства. Линейная комбинация и линейная зависимость системы векторов.
Отрезок на прямой определяется двумя равноправными точками – его концами.Различают также направленный отрезок, т.е. отрезок, относительно концов,которого известно какой из них первый (начало), а какой – второй (конец). Направленный отрезок (или упорядоченная пара точек)
называется вектором.
Вектор обычно обозначается
символом
![]() ,
где А – начало, а В – конец направленного
отрезка, либо одной буквой
,
где А – начало, а В – конец направленного
отрезка, либо одной буквой
![]() .
Расстояние между началом и концом
вектора называется его длиной. Для
обозначения длины вектора (его абсолютной
величины) пользуются символом модуля.
Так
.
Расстояние между началом и концом
вектора называется его длиной. Для
обозначения длины вектора (его абсолютной
величины) пользуются символом модуля.
Так
![]()
и
![]() обозначают
длины соответствующих векторов.
обозначают
длины соответствующих векторов.
Векторы расположенные либо на одной прямой, либо на параллельных прямых называются коллинеарными. Нулевой вектор считается коллинеарным любому вектору. Среди коллениарных векторов различают одинаково направленные (сонаправленные) и противоположно направленные векторы. Векторы называются компланарными, если они лежат либо на одной плоскости, либо на прямых, параллельных одной и той же плоскости.
Понятие равенства векторов обладает следующими свойствами:
1.
![]() (рефлексивность).
(рефлексивность).
2. Из того, что
![]() ,
следует
,
следует
![]() (симметричность).
(симметричность).
3. Из того, что
и
![]() ,
следует
,
следует
![]() (транзитивность).
(транзитивность).
Суммой
![]()
двух векторов и называется
вектор, имеющий начало в начале вектора
,
а конец – в конце вектора
![]() ,
,
при условии, что вектор приложен к концу вектора В соответствии с определением слагаемые
и и их сумма образуют треугольник (рис.2). Поэтому данное правило сложения двух векторов
называют «правилом треугольника».
Операция сложения векторов обладает свойствами:
1.
![]() (коммутативность);
(коммутативность);
2.
![]() ,
(ассоциативность);
,
(ассоциативность);
3.
![]() для
любого вектора
(особая
роль нулевого вектора);
для
любого вектора
(особая
роль нулевого вектора);
4.для каждого вектора
существует противоположный ему вектор
![]() такой,
что
такой,
что
![]() (для
получения
достаточно
поменять местами начало и конец вектора
).Вектор
противоположный вектору
обозначают
(для
получения
достаточно
поменять местами начало и конец вектора
).Вектор
противоположный вектору
обозначают
![]() .
.
Разностью
![]() векторов
и
называется сумма вектора
ивектора
противоположного вектору
векторов
и
называется сумма вектора
ивектора
противоположного вектору
, т.е.
![]() .
.
Разность
получается
из вектора
сдвигом
его начала в конец вектора
,
при условии, что векторы
и
имеют
общее начало (рис.3). Очевидно, что
![]()
для любого вектора .
Замечание: Существует еще одно правило сложения векторов, называемое
«правилом параллелограмма»: векторы и прикладываются к общему
началу О, и на них строится
параллелограмм (рис. 4). Суммой
будет
вектор
![]() ,
расположенный на диагонали параллелограмма.
Разностью
здесь будет вектор
,
расположенный на диагонали параллелограмма.
Разностью
здесь будет вектор
![]() ,
,
расположенный на второй диагонали.
Произведением
![]() вектора
на
вещественное число λ (скаляр) называется
вектор
,
такой, что 1)
вектора
на
вещественное число λ (скаляр) называется
вектор
,
такой, что 1)
![]() ;
2) вектор
коллинеарен вектору
;
3)векторы
и
имеют
одинаковое (противоположное) направление
если λ > 0 (λ <0).
;
2) вектор
коллинеарен вектору
;
3)векторы
и
имеют
одинаковое (противоположное) направление
если λ > 0 (λ <0).
Замечание: В случае, когда
λ = 0 или
![]() произведение
является нулевым вектором.
произведение
является нулевым вектором.
Операция умножения вектора на число обладает следующими свойствами:
1.
![]() (ассоциативное
свойство сомножителей);
(ассоциативное
свойство сомножителей);
Действительно, заметим, что
векторы, стоящие обеих частях равенства,
имеют одну и ту же длину
![]() .
Кроме того, они коллинеарны и одинаково
направлены, так как их направление
совпадает с
.
Кроме того, они коллинеарны и одинаково
направлены, так как их направление
совпадает с
направлением , если λ и μ одного знака, и противоположно направлению , если λ и μ имеют разные знаки. Если же λ или μ равны нулю,то обе части равенства равны нулю. Свойство доказано.
2.
 (свойства
дистрибутивности).
(свойства
дистрибутивности).
Теорема: Если вектор коллинеарен ненулевому вектору , то существует вещественное число λ такое, что = λ .
Линейная зависимость векторов
Любое
множество, элементами которого являются
векторы, называется системой векторов.
Выражение вида
![]() ,
где λ i – вещественное число, называется
линейной комбинацией векторов системы
,
где λ i – вещественное число, называется
линейной комбинацией векторов системы
![]()
.
Числа λ i называются коэффициентами
линейной комбинации. Если
![]() ,
то говорят, что вектор
представлен
(разложен) в виде линейной комбинации
векторов системы
,
то говорят, что вектор
представлен
(разложен) в виде линейной комбинации
векторов системы
5. Признак линейной зависимости. Коллинеарность двух векторов. Теоремы о разложении векторов. Признак компланарности трех векторов пространства. Базисы. Координаты векторов. Теорема о координатах линейной комбинации векторов и действия с векторами в координатах. Признак коллинеарности двух и компланарности трех векторов в координатах.
Признак коллинеарности Если существует такое число k при котором выполняется равенство a k b и при том вектор b 0 , то векторы a и b коллинеарны.
Ба́зис (др.-греч. βασις, основа) — множество таких векторов в векторном пространстве, что любой вектор этого пространства может быть единственным образом представлен в виде линейной комбинации векторов из этого множества — базисных векторов.
В случае, когда базис бесконечен, понятие «линейная комбинация» требует уточнения. Это ведёт к двум основным разновидностям определения:
Базис Га́меля, в определении которого рассматриваются только конечные линейные комбинации. Базис Гамеля применяется в основном в абстрактной алгебре (в частности в линейной алгебре).
Базис Ша́удера, в определении которого рассматриваются и бесконечные линейные комбинации, а именно — разложение вряды. Это определение применяется в основном в функциональном анализе, в частности для гильбертова пространства,
В конечномерных пространствах обе разновидности базиса совпадают.
Координа́ты ве́ктора ― коэффициенты единственно возможной линейной комбинации базисных векторов в выбранной системе координат, равной данному вектору.
![]() ,
,![]() ,где
,где ![]() —
координаты вектора.
—
координаты вектора.
Равные векторы в единой системе координат имеют равные координаты
Координаты коллинеарных векторов пропорциональны:
![]()
Подразумевается, что
координаты вектора ![]() не
равны нулю.
не
равны нулю.
Квадрат длины вектора равен сумме квадратов его координат:
![]() При
умножении вектора на действительное
число каждая его координата умножается
на это число:
При
умножении вектора на действительное
число каждая его координата умножается
на это число:![]()
При сложении векторов соответствующие координаты векторов складываются:
![]()
Скалярное
произведение двух векторов равно
сумме произведений их соответствующих
координат:![]()
Векторное произведение двух векторов можно вычислить с помощью определителя матрицы
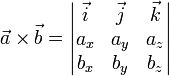
Теорема о координатах линейной комбинации векторов. Каждая координата вектора = линейной комбинации векторов { }, заданной своими координатами в базисе { }, равна той же линейной комбинации соответствующих координат составляющих векторов.
1.умножение на число: произведение вектора А на число l наз. такой вектор В, который обладает след. св-ми: а) А||В. б) l>0, то АВ, l<0, то А¯В. 2. Разделить вектор на число n значит умножить его на число, обратное n: а/n=a*(1/n).3.Суммой неск-их векторов а и в наз. соединяющий начало 1-го и конец последнего вектора. 4. Разностью векторов а и в наз-ся вектор c, который, будучи сложенным с вектором в даст вектор а.
Признак коллинеарности двух векторов в координатах:Необходимое и достаточное условие коллинеарности двух векторов в дальнейшем используется, например, для доказательства теоремы о разложении вектора пространства по трем некомпланарным векторам, для вывода параметрических уравнений прямой и т.д.
|
Три вектора компланарны если будучи приведены к общему началу лежат в одной плоскости, если определитель составленный из координат векторов равен 0.
