Предположим противное, т.Е. Ряд сходитсяпротиворечие с Кошиневерно Доказать расходимость гармонического ряда
- доказать расходимость
Оценим |Snm|=1/(n+1)+1/(n+2)+…+1/(n+m)m/(n+m)
n(n)=n+1, m(n)=n+1
№7
Знакоположительные ряды. Теорема о существовании
Суммы знакоположительного ряда. Вывести условия сходимости эталонного ряда.
Знакоположительные ряды:
(1)
называется знакоположительным, если
Замечание:
Т.к.
=
+
=A+
=A+
(
и
имеют одинаковый характер)
Теорема о существовании суммы знакоположительного ряда:
Знакоположительный
ряд (1) всегда имеет сумму, причём она
конечна, а ряд (1) сходится, если Sn
этого ряда ограничена сверху, и бесконечна
в +,
а ряд (1) расходится, если Sn
не ограничена сверху.
Доказательство:
1)Sn+1=a1+a2+…+an+an+1=Sn+an+1Sn, тогда {Sn} монотонно возрастает и по условию ограничена сверху. По теореме о lim у монотонно возрастающей ограниченной сверху последовательности следует, что последовательность сходится: limSn=S – конечное число при n+
2)если монотонно возрастающая последовательность не ограничена сверху, то по той же теореме такая последовательность имеет limSn= при n+ряд расходится
Условие сходимости эталонного ряда:
сходится
при p>1
+
<
+
=
=
+
+
+
<
+
+
+
=
=
=
+…+
<
=
…
+
+…+
<
=
=
1+
<
=
,
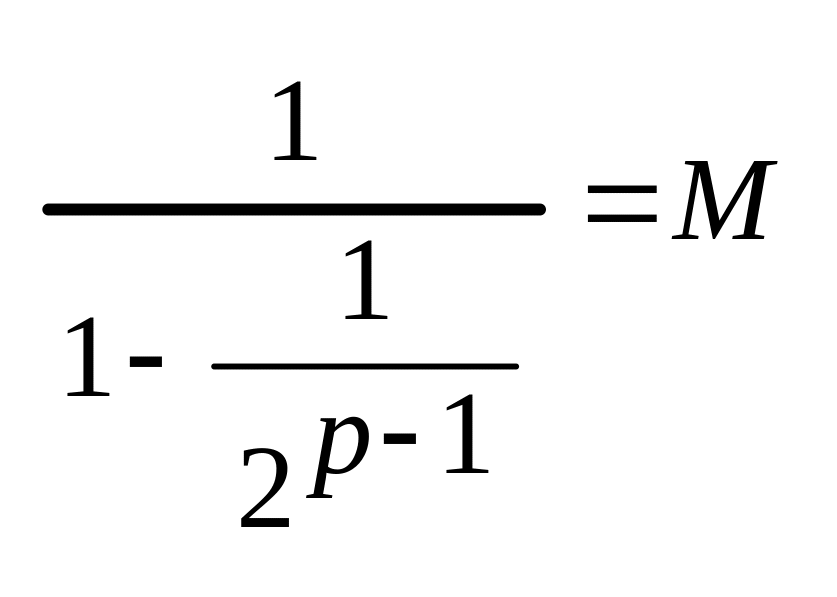0<
<1
По теореме 1 ряд сходится и имеет конечную сумму.
№8 Признак сравнения общий и предельный для знакоположительных рядов.
Общий признак сравнения:
Рассмотрим (1) и (2), для которых выполнено:(nN):anbn, an0, bn0, тогда:
1)из сходимости ряда (2) следует сходимость (1)
2)из расходимости ряда (1) следует расходимость (2)
Доказательство:
1)т.к. (2) – сходится, то limSn*=S*(nN):Sn*<S*
0Sn=a1+a2+…+anb1+b2+…+bn=Sn*<S*S* ограничена сверху S*(1) – сходится
2)ряд (1) - расходится{Sn} – не ограничена сверхуlimSn=+ при n+
0SnSn*{Sn*} – не ограничена сверхуlimSn*=+ при n+(2) – расходится к +.
Предельный признак сравнения:
Пусть (1) и (2) таковы, что:
1)(nN):an>0, bn>0
2)liman/bn=K при n+ (0K +), тогда:
1)из сх. (2) при 0K<+ следует сх. ряда (1)
2)из расходимости (2) при 0<K + следует расходимость (1)
3)при 0<K<+ (конечном) (1) и (2) имеют одинаковый характер
Доказательство:
1)0K<+,
то
liman/bn=K
при
n+
(K-)bn<an<(K+)bn
т.к.
(2) – сходится, то по свойству (2)
- сходится, но
an<(K+)bnan
– сходится
2)
0<K
+,
то
limbn/an=K1
при
n+
(0K1<
+)
(K1=1/K)
(K1-)an<bn<(K1+)an
-
расходится, т.к. bn
- расходится
- расходится по свойству 2.
3)следует из 1 и 2
№9 Признак Коши и Даламбера.
Признак Коши:
Рассмотрим
(1) и положим
при n+,
тогда:
1)если <1, то (1) – сходится
2)если >1, то (1) – расходится
3)=1, то (1) может быть как сходящимся, так и расходящимся
Доказательство:
1)<1, выберем <<1
Т.к.
- верхний предел, то
:
,
0<<1
=/(1-)
– сходится
2)>1{ank}
– подпоследовательность, что
при n+
liman0
при n+
an
– расходится
3)
и
,
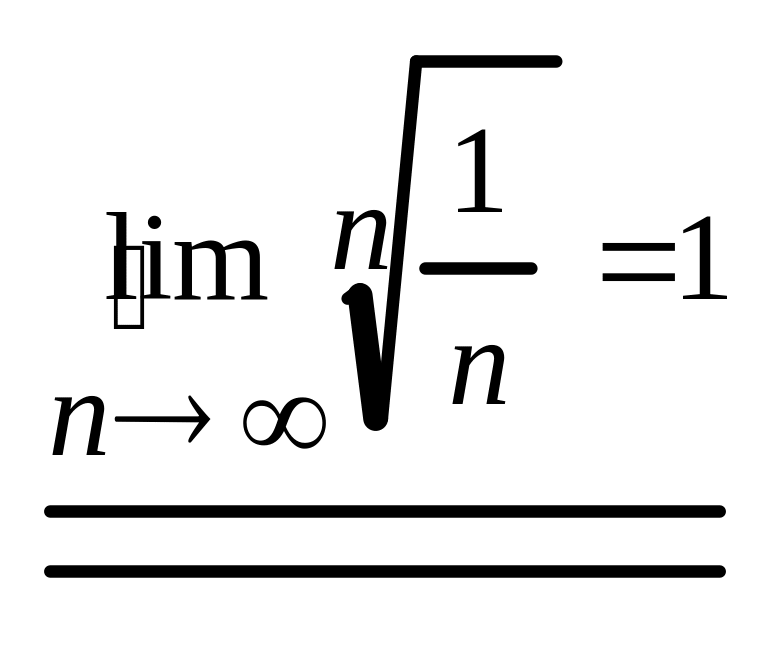но
- сходится
,
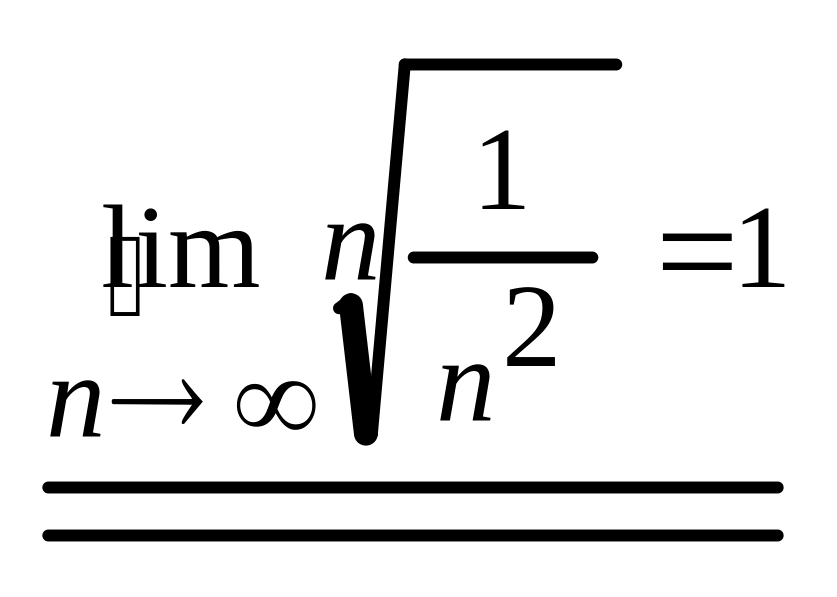но
- расходится
Признак Даламбера:
Рассмотрим
(1) an>0
и положим
при n+,
тогда:
1)если <1, (1) – сходится
2) >1, (1) – расходится
3) =1, (1) – сходится или расходится
Доказательство:
1)<1,
<<1,
:
…
-
сходится, тогда
- сходится
- сходится
2)>1,
:
liman0
при
n+
3) и
,
но ряд расходится
,
но ряд сходится
№10 Интегральный признак сходимости знакоположительных рядов.
Для an=f(n)>0 выполняется:
1)(x1): f(x) – не возрастающая положительная функция, тогда (1) :
1)сходится,
если
- сходится
2)расходится, если - расходится
Доказательство:
Т.к.
f(x)>0
– не возрастающая, то x[n,n+1]:
Просуммируем, n=1, 2…
a2+a3+…+an+1
a1+a2+…+an=Sn
Sn+1-a1
Sn
возрастающая последовательность {Sn}
и {
}
одновременно либо имеют конечный
предел, либо бесконечный.
11. Определение знакопеременного ряда. Абсолютная и условная сходимость. Признак Дирихле
Опред:1 Числовой ряд (1) называется знакопеременным , если (nN)(n1(n) N, n2(n), N , n1(n)>n n2(n)>n): an1(n)>0, an2(n)<0
Опред2: Ряд (1) называется знакопеременным если он содержит как бесконечное множество положительных членов так и бесконечное множество отрицательных.
Опред3:
Знакопеременный ряд (1) – абсолютно
сходится если сходится ряд
как
знакоположительный ряд.
Опред4: Ряд(1) называется условно сходящимся если он сам сходится, а ряд из абсолютных величин расходится.
Теор. (Признак Дирихле)
Рассмотрим
знакопеременный ряд (2)
и выполняется :
(M>0)( (nN): | Sn|≤M, где Sn=
(частичная сумма)Последовательность bn – монотонно убывающая знакоположительная последовательность.
3)
lim
bn=0
(при n)
Тогда ряд (2) – сходится в общем случае условно.
Док-во: Докажем предварительно тождество Абеля:
Если p,q N 1≤p≤q то тогда справедливо :
,
где S0=0
Док-во:
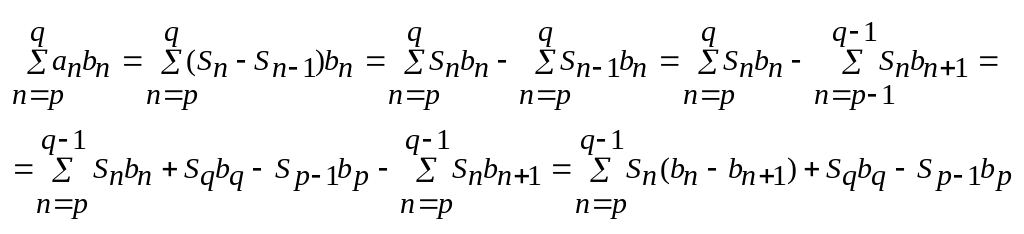
Докажем теперь сам признак Дирихле.
Так как lim bn по условию 3) равен 0 то
(limbn=0(при n)) ((>0)(n0()N)( n>n0()): bn</2M
воспользуемся критерием Коши
(p,qN, p>n0(), q> n0()): оценим:
Согласно критерию Коши этот ряд- сходится.