5.2 Получение синусоидальной эдс

Синусоидальную ЭДС можно получить, вращая с постоянной частотой в равномерном магнитном поле проводник в виде прямоугольной рамки.

М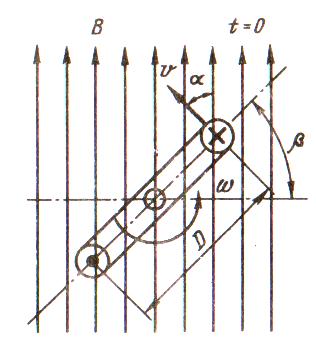 ы знаем, что в рамке, имеющей 2 активных проводника длиной l :

e = 2Bvl sinα (5.3)

При равномерном вращении рамки линейная скорость проводника не изменяется:

(5.4)

а угол между направлением скорости и направлением магнитного поля изменяется пропорционально времени:

β = α = ωt (5.5)

Угол β определяет положение рамки относительно плоскости, перпендикулярной направлению магнитной индукции. В момент t = 0 положение рамки характеризуется углом β = 0. ЭДС в рамке является синусоидальной функцией времени:

e = BlDω sin ωt (5.6)

Наибольшая ЭДС получается при угле 90^о:

Е_m = BlDω (5.7)

Следовательно мгновенное значение ЭДС:

e = Е_m sinωt (5.8)

Мгновенное значение переменной величины есть функция времени. Ее принято обозначать строчной буквой:

i  - мгновенное значение тока i(t);

u - мгновенное значение напряжения u(t);

e - мгновенное значение ЭДС e(t) ;

p - мгновенное значение мощности p(t).

Наибольшее мгновенное значение переменной величины за период называется амплитудой (ее принято обозначать заглавной буквой с индексом m).

I_m - амплитуда тока;

U_m - амплитуда напряжения;

E_m - амплитуда ЭДС.

5.3 Изображение синусоидальных эдс, напряжений и токов на плоскости декартовых координат

Синусоидальные токи и напряжения можно отобразить графически, записать при помощи уравнений с тригонометрическими функциями, представить в виде вращающихся векторов и отобразить с помощью комплексных чисел.

Приведенным на рис. 5.1 и 5.2 графикам двух синусоидальных ЭДС е₁ и е₂ соответствуют уравнения:

e₁ = E_1m sin(ωt + ψ_e1); e₂ = E_2m sin(ωt + ψ_e2); (5.9)

Значения аргументов синусоидальных функций (ωt + ψ_e1) и (ωt + ψ_e2) называются фазами синусоид, а значения фазы в начальный момент времени (t=0): ψ_e1 и ψ_e2 - начальными фазами (для представленных графиков ψ_e1 >0; ψ_e2<0).

Величину ω, характеризующую скорость изменения фазового угла, называют угловой частотой. Так как фазовый угол синусоиды за время одного периода Т изменяется на 2π рад., то угловая частота определяется:

(5.10)

При совместном рассмотрении двух синусоидальных величин одной частоты разность их фазовых углов, равную разности начальных фаз, называют углом сдвига фаз.

Для синусоидальных ЭДС е₁ и е₂ угол сдвига фаз:

φ = (ωt + ψ_e1) - (ωt + ψ_e2)= ψ_e1 - ψ_e2 (5.11)

5.4 Векторное изображение синусоидально изменяющихся величин. Векторные диаграммы.

До сих пор мы с вами синусоидальные величины изображали графически или записывали их формулы. Есть еще один способ отображения синусоиды – вращающийся вектор.

Пусть переменный ток задан уравнением

i = I_m sin (ωt + ψ) (5.12)

Проведем две взаимно-перпендикулярные оси и из точки пересечения осей построим вектор. Длину этого вектора, в определенном масштабе, приравняем амплитуде I_m. Направление вектора пусть определяется начальной фазой рассматриваемого тока ψ. Рядом нарисуем декартовые оси координат i = f(ωt). Спроецируем наш вектор на ось i. Проекция будет равна

i₀ = I_m sin ψ (5.13)

Теперь начнем вращать вектор против часовой стрелки с угловой частотой ω. Тогда положение вектора в любой момент времени будет определяться углом

ωt + ψ.

Для времени t₁ проекция вектора на ось i будет равна:

i₁ = I_m sin (ωt₁ + ψ) (5.14)

Для времени t_n:

i_n = I_m sin (ωt_n + ψ) (5.15)

и так далее.

В общем случае:

i = I_m sin (ωt + ψ) (5.16)

Таким образом, формула, описывающая проекцию вращающегося вектора длиной I_m такая же, что и формула мгновенного значения тока. Это и позволяет нам изображать переменные синусоидальные величины в виде вращающихся векторов.

Это подтверждается и тем, что вращая наш вектор против часовой стрелки можно построить график изменения указанной проекции во времени. Получим синусоиду в пределах одного оборота, см. рис. 5.3

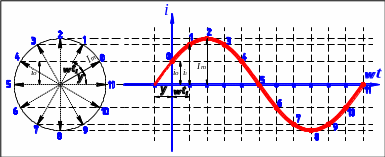
Рис. 5.3 Построение синусоиды с помощью вращающегося вектора

При построении векторов положительным направлением считается движение против часовой стрелки.

Е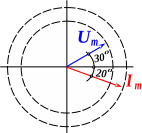 сли на одном чертеже изобразить несколько векторных величин одной частоты – получим векторную диаграмму. Например, напряжение и ток конкретной электрической цепи выражаются уравнениями:

u = 125 sin (ωt + 30⁰) (5.17)

i = 12 sin (ωt -20⁰) (5.18)

Рис. 5.4 Векторная диаграмма

Если выбрать масштабы напряжения и тока М_U = 50 В/см; М_I = 4 А/см, получим длину вектора напряжения 2,5 см; вектора тока 3 см – смотри рис. 5.4.

На векторной диаграмме изображают переменные величины одной частоты, поэтому их взаимное расположение не меняется. Начало отсчета времени выбирается произвольно. Поэтому один из векторов чертится произвольно, остальные – с учетом сдвига фаз.

Векторные диаграммы очень удобны для сложения и вычитания синусоидальных величин. Требуется, например сложить два тока:

i₁ = I₁ sin (ωt + ψ₁); i₂ = I₂ sin (ωt + ψ₂) (5.19)

Сумма токов:

i = I₁ sin (ωt + ψ₁) + I₂ sin (ωt + ψ₂) (5.20)

– громоздко и ненаглядно.

Можно начертить синусоиды токов в одной системе координат и для ряда аргументов найти сумму токов. Если соединить полученные значения, получится синусоида. Этот способ тоже неудобен.

Гораздо проще складывать и вычитать вектора на векторных диаграммах. Для этого нужно знать правила сложения векторов. Вы их прекрасно знаете из школьной программы.

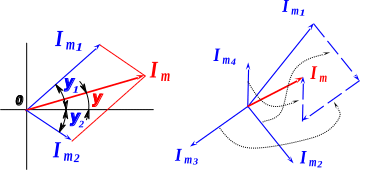
Рис 5.5 Сложение векторов