5.2.2. Схема доказательства правильности конечного автомата

Схема доказательства правильности конечного автомата такова:

1) определить (описать) для каждого состояния q Q язык L(q),состоящий из слов, переводящих начальное состояние q₀ в q;

2) доказать, что это определение правильное, используя индукцию по длине входного слова;

3) показать, что .

Применим эту схему к доказательству правильности, построенного выше автомата A. Языки, связанные с состояниями этого автомата, фактически, уже были определены при его построении. Уточним их:

L(q₀) = {ε},

L(q₁) = {a},

L(q₂) = {w | слова, начинающиеся с aa и содержащие четное число букв b},

L(q₃) = L,

L(q_!) = {w | слова, не начинающиеся с aa}.

Правильность определения языков L(q₀), L(q₁) и L(q₁) следует непосредственно из определения A. Самое короткое слово, переводящее q₀ в q₂aa, и оно принадлежит L(q₂). Аналогично, самое короткое слово, переводящее q₀ в q₃ aab, и оно принадлежит L(q₃). Предположим теперь, что для каждого слова w длины ≤ n выполнено условие(*):

Покажем, что оно будет выполнено и для всех слов длины n + 1.

Пусть|w|=n+1. Тогда w=w^’α, где α {a, b}. Так как |w^’| = n, то для w^’выполнено условие (*). Поэтому, если w’ переводит q₀ в q₂, то это слово начинается с aa и содержит четное число b. При α = a слово w переводит q₀ в q₂ и также начинается с aa и содержит четное число b, а при α = b слово w переводит q₀ в q₃, начинается с aa и содержит нечетное число b, т.е. принадлежитL.

Аналогично, если w’ переводит q₀ в q₃, то это слово начинается с aa и содержит нечетное число b. При α =a слово w также переводит q₀ в q₃ и также начинается с aa и содержит нечетное число b, а при α = b w переводит q₀ в q₂, оно начинается с aa и содержит четное число b. Обратно, если α= a, то слово w переводит q₀ в q_i (i = 2, 3) w^’переводит q₀ в q_i(i = 2, 3) и условие (*) выполнено, так как четность числа букв b в w и в w’ одинакова. Если же α = b , то из определения автомата A следует, что слово w переводит q₀в q₂ w’ переводит q₀ в q₃и w переводит q₀в q₃ w^’переводит q₀ в q₂. Так как четность числа букв b в w и в w⁰разная, то и в этом случае условие (*) выполнено. Для завершения доказательства осталось заметить, что единственным заключительным состоянием автомата A является q₃ и поэтому L_A= L(q₃) = L.

5.2.3. Произведение автоматов

Рассмотрим одну важную конструкцию конечного автомата по двум другим, называемую произведением автоматов, которая позволит установить замкнутость класса конечно автоматных языков относительно теоретико множественных операций.

Пусть M₁=< Σ, Q₁, ^{, ,}Φ₁> и M₂=< Σ, Q₂, _{, F}2^,Φ₂> два конечных автомата с общим входным алфавитом Σ, распознающие языки L₁ и L₂, соответственно.

Определим по ним автомат M=< Σ, Q, q₀, F, Φ >, называемый произведением M₁ и M₂(M = M₁хM₂), следующим образом. Q = Q₁хQ₂= {(q, p) | q Q₁, p Q₂}, т.е. состояния нового автомата это пары, первый элемент которых состояние первого автомата, а второй состояние второго автомата. Для каждой такой пары (q, p) и входного символа a Σ определим функцию переходов: Φ((q, p), a) =(Φ₁(q, a), Φ₂(p, a)). Начальным состоянием M является пара q₀= ( _, ), состоящая из начальных состояний автоматов-множителей. Что касается множества заключительных состояний, то оно определяется в зависимости от операции над языками L₁ и L₂, которую должен реализовать M .

Теорема 1.

а) При автомат M=<Σ, Q, q0, , Φ> распознает язык L = L₁ L₂.

б) При F∩⁼{(q, p) | q F₁ и p F₂} автомат M =< Σ, Q, q₀, F∩^,Φ > распознает язык L = L₁∩ L₂.

в) При F_\= {(q, p) | q F₁ и p F₂} автомат M =< Σ, Q, q₀, F_\, Φ > распознает язык L = L₁\ L₂.

Доказательство этой теоремы непосредственно выводится из следующего утверждения.

Лемма 2. Для любых двух состояний (q, p) и (q^’, p^’) автомата M и любого входного слова w слово w переводит (q, p) в (q^’, p^’) в автомате M тогда и только тогда, когда оно переводит q в q^’ в автомате M₁ и p в p^’в автомате M₂.

Лемма устанавливается индукцией по длине слова w.

Следствие. Класс конечно автоматных языков замкнут относительно теоретико множественных операций объединения, пересечения и разности.

Вопросы для повторения

1.Детерминированный конечный автомат это?

2.Что называется диаграммой автомата?

3.Под программой автомата понимается?

4.В каком случае язык называется конечно-автоматным?

Резюме по теме

Приведены основные понятия детерминированных конечных автоматов. Выявлено понятие программы автомата, а так же диаграммы и конфигурации детерминированного автомата. Рассмотрена схема доказательства правильности автомата, которая позволяет судить о работоспособности автомата. Продемонстрировано произведение автомата.

Тема 5.3. Недетерминированные конечные автоматы

Цель: ознакомиться с недетерминированными конечными автоматами и способом их детерминизации.

Задачи:

1. Рассмотреть недетерминированные конечные автоматы.

2. Рассмотреть детерминизацию недетерминированного конечного автомата.

5.3.1. Основные понятия недетерминированных конечных автоматов

Рассматриваемые недетерминированные конечные автоматы являются обобщениями детерминированных: они при чтении очередного символа на входе могут выбрать в качестве следующего одно из нескольких состояний, а кроме того, могут изменить состояние без чтения входа. Основной результат, который мы установим, утверждает, что это обобщение не существенно: недетерминированные и детерминированные конечные автоматы распознают одни и те же языки.

Недетерминированный конечный автомат (НКА) - распознаватель - это система вида

M =< Σ, Q, q₀, F, Φ >,

включающая следующие компоненты:

Σ = {a₁, . . . , a_m} (m ≥ 1) конечное множество - входной алфавит;

Q = {q₀, . . . , q_n−1^}(n ≥ 1) конечное множество - алфавит внутренних состояний;

q₀ Q начальное состояние автомата;

F Q множество принимающих (допускающих, заключительных) состояний;

Φ :Q Ч (Σ {ε}) → 2^Q функция переходов. Для a Σ значение Φ(q, a) - это множество состояний в каждое из которых может перейти автомат из состояния q, когда получает на вход символ a. Φ(q, ε) - это множество состояний в каждое из которых может перейти автомат из состояния q без чтения символа на входе.

Как и для детерминированных автоматов, функцию переходов можно представить с помощью набора команд-программы: для каждой пары q Q и a Σ и каждого состояния q^’ Φ(q, a) в программу помещается команда qa → q^’, и для каждого состояния q^’ Φ(q, ε) в программу помещается команда q → q^’. Отличие от детерминированного случая состоит в том, что для одной пары q Q и a Σ в программе может быть несколько команд вида qa → q^’ или не быть ни одной такой команды. Кроме того, могут появиться ε-команды (пустые переходы) вида q → q^’, означающие возможность непосредственного перехода из q в q^’ без чтения символа на входе.

При табличном задании функции Φ в таблице появляется (m + 1)-ый столбец, соответствующий пустому символу ε и на пересечении строки q и столбца a (Σ {ε})стоит множество состояний Φ(q, a).

Для недетерминированного автомата M =<Σ, Q, q₀, Φ > в диаграмме D_M=(Q, E) с выделенной начальной вершиной q₀ и множеством заключительных вершин F ребра взаимно однозначно соответствуют командам: команде вида qa → q^’ (a Σ) соответствует ребро (q, q^’), с меткой a, а команде вида q → q^’ cоответствует ребро (q, q^’), с меткой ε.

Скажем, что заданный последовательностью ребер путь p = e₁e₂. . . e_T в диаграмме D_M несет слово w = w₁w₂. . . w_t (t ≤ T ), если после удаления из него пустых ребер (т.е. ребер с метками ε) остается последовательность из t ребер p^’= метки которых образуют слово w, т.е. w_i это метка ребра 1(≤i≤t). Очевидно, это эквивалентно тому, что последовательность меток на ребрах пути p имеет вид , где k_j≥ 0 (j = 1, 2, . . . , t + 1) и t + .

Слово w переводит q в q^’в диаграмме D_M, если в ней имеется путь из q в q^’ который несет w.

На недетерминированные автоматы естественным образом переносится определение конфигураций и отношения перехода между ними.

Конфигурация НКА M =< Σ, Q, q₀, F, Φ, > - это произвольная пара вида (q, w), в которой q Q и w . Определим отношение _M перехода из одной конфигурации в другую за один шаг :

(q, w) _M(q’, w’) (w = aw’ и q’ Φ(q, a)) или (w = w’ и q’ Φ(q, ε)).

Как и для ДКА, через _M обозначим рефлексивное и транзитивное замыкание отношения _M.

Внешне определение распознавания слов НКА совпадает с определением для ДКА.

НКА M распознает (допускает, принимает) слово w, если для некоторого q F (q’, w) _M(q, ε) .

Язык L_M, распознаваемый НКА M, состоит из всех слов, распознаваемых автоматом:

L_M= {w | M распознает w}.

Отличие состоит в том, что у НКА может быть несколько различных способов работы (путей вычисления) на одном и том же входном слове w. Считаем, что НКА распознает (допускает, принимает) это слово, если хотя бы один из этих способов приводит в заключительное состояние из F .

Из определения диаграммы D_M непосредственно следует, что НКА M распознает слово w, тогда и только тогда, когда существует такое заключительное состояние q F , что в диаграмме D_M слово w переводит q₀ в q. Иными словами, в D_M имеется путь из q₀ в q, на ребрах которого написано слово w ( с точностью до меток ε).

П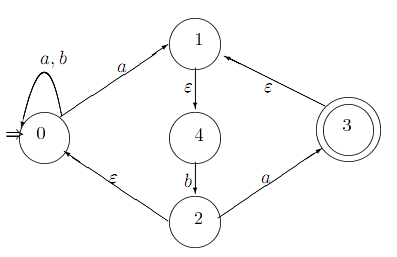 ример 1. Рассмотрим НКА N₁=<{a,b},{0,1,2,3,4},0,{3},Φ>, где его диаграмма D_N1 представлена на рис. 5.15.

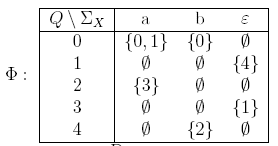
Рис. 5.15. Таблица функции переходов и диаграмма НКА

Рассмотрим работу этого автомата на слове ababa:

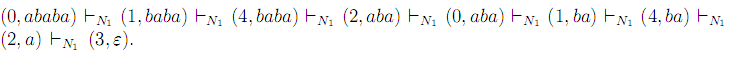
Так как 3 - заключительное состояние, то ababa L_N1^. Заметим, что у автомата N₁ имеются и другие способы работы на этом слове, не ведущие к заключительному состоянию. Например, он может после чтения каждого символа оставаться в состоянии 0. Но чтобы слово допускалось, достаточно существовать хотя бы одному хорошему способу.