3.2.2. Полиномиальная формула

- полиномиальная формула. Суммирование в ней производится по всем решениям уравнения n₁+n₂+…+n_k=n в целых неотрицательных числах.

Теорема о полиномиальных коэффициентах. .

Пример 5.

Определим коэффициент с в слагаемом полинома (с приведенными подобными членами), получаемого из выражения .

В силу теоремы о полиномиальных коэффициентах .

3.2.3. Формула включений и исключений

Часто комбинаторная конфигурация является объединением других, число комбинаций в которых вычислить проще. В таком случае требуется уметь вычислять число комбинаций в объединении.

Пусть А₁ и А₂ – 2 конечных множества. Тогда если А₁А₂=, то . Пусть теперь А₁А₂, тогда в каждый элемент из А₁А₂ будет учтен дважды. Поэтому . Последнюю формулу можно обобщить на случай произвольного числа множеств:

. (2)

Р

авенство (2) называется формулой включений и исключений. В частности, для трех множеств эта формула имеет вид:

.

Доказывается формула (1) методом математической индукции.

Пример 6.

Сколько существует натуральных чисел, меньших 1000, которые не делятся ни на 3, ни на 5, ни на 7?

Всего чисел, меньших тысячи, 999. Из них 999:3=333 делятся на 3,

999:5=199 (ост. 4) делятся на 5,

999:7=142 (ост. 5) делятся на 7,

999:(3х5)=66 (ост. 9) делятся на 3 и на 5,

999:(3х7)=47 (ост. 12) делятся на 3 и на 7,

999:(5х7)=28 (ост. 10) делятся на 5 и на 7,

999:(3х5х7)=9 (ост. 45) делятся на 3, на 5 и на 7.

В итоге искомых чисел 999-(333+199+142-66-47-28+9)=457.

Следствие. Пусть А – конечное множество, А₁, …, А_n – его подмножества. Тогда

. (3)

Доказательство. Поскольку , а , то . Следовательно, . Применив для правой части последнего равенства формулу включений и исключений, получим искомый результат.

Пример 7.

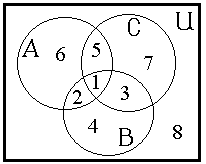
Дано множество А={0, 1, …, 10} и 3 его подмножества: А₁={a | a – четное}, А₂={a | a>6}, А₃={a | 2<a<8}. Сколько элементов множества А не принадлежат ни одному из этих подмножеств?

тогда по формуле (3) . Очевидно, что таким элементом является 1.

Вопросы для повторения

1.Что такое разбиение?

2.Запишите полиномиальную формулу?

3.О чем говорится в теореме о полиномиальных коэффициентах?

4.Как выглядит формула включений и исключений?

5.Для чего необходима формула включений и исключений?

Резюме по теме

Рассмотрено понятие разбиения. Приведены необходимые теоремы разбиения. Показана полиномиальная формула, а так же приведена теорема о полиномиальных коэффициентах. Рассмотрены формулы включений и исключений.

Глава 4. Теория графов

Теория графов — раздел дискретной математики, изучающий свойства графов. В общем смысле граф представляется как множество вершин (узлов), соединённых рёбрами. В строгом определении графом называется такая пара множеств G={R,V}, где V есть подмножество любого счётного множества, а R - подмножество V×V.

Теория графов находит применение, например, в геоинформационных системах (ГИС). Существующие или вновь проектируемые дома, сооружения, кварталы и т. п. рассматриваются как вершины, а соединяющие их дороги, инженерные сети, линии электропередач и т. п. — как рёбра. Применение различных вычислений, производимых на таком графе, позволяет, например, найти кратчайший объездной путь или ближайший продуктовый магазин, спланировать оптимальный маршрут.

Родоначальником теории графов считается Леонард Эйлер. В 1736 году в одном из своих писем он формулирует и предлагает решение задачи о семи кёнигсбергских мостах, ставшей впоследствии одной из классических задач теории графов.

Терминология теории графов поныне не определена строго. В частности в монографии Гудман, Хидетниеми, 1981 сказано «В программистском мире нет единого мнения о том, какой из двух терминов «граф» или «сеть».

При изображении графов чаще всего используется следующая система обозначений: каждой вершине сопоставляется точка на плоскости, и если между вершинами существует ребро, то соответствующие точки соединяются отрезком. В случаи ориентированного графа отрезки заменяют стрелками.

Не следует путать изображение графа с собственно графом (абстрактной структурой), поскольку одному графу можно сопоставить не одно графическое представление. Изображение призвано лишь показать какие пары вершин соединены ребрами, а какие - нет. Часто на практике бывает трудно ответить на вопрос - являются ли два изображения моделями одного и того же графа, или нет. В зависимости от задачи, одни изображения могут давать более наглядную картину, чем другие.

Теория графов решает такие задачи как: семь мостов Кёнигсберга — один из первых результатов в теории графов, опубликован Эйлером в 1736; проблема четырёх красок — была сформулирована в 1852 году, но доказательство получено лишь в 1976 году (достаточно 4-х красок для карты на сфере (плоскости)); задача коммивояжёра — одна из наиболее известных NP-полных задач; задача о клике — ещё одна NP-полная задача; нахождение минимального стягивающего дерева.

В настоящее время на языке теории графов формулируются и решаются многие задачи управления, в том числе задачи сетевого планирования и управления, анализа и проектирования организационных структур управления, анализа процессов функционирования и целеполагания, многие задачи принятия решений в условиях неопределенности и др.

Гипотеза Улама - а) всякий граф с более чем двумя вершинами однозначно определяется набором графов, где каждый граф из набора получен удалением одной из вершин исходного графа. б) всякий граф с более чем тремя вершинами однозначно определяется множеством графов, где каждый граф из множества получен удалением одной из вершин исходного графа. (Иными словами, не существует таких двух различных графов для которых бы эти наборы или множества совпадали).