
- •Введение в дискретный анализ
- •Глава 1. Введение в теорию множеств
- •Тема 1.1. Множества и операции над ними
- •1.1.1. Основные понятия
- •1.1.2. Операции над множествами
- •1.1.3. Векторы и прямые произведения
- •Вопросы для повторения
- •Резюме по теме
- •Тема 1.2. Отношения
- •1.2.1. Основные понятия и определения
- •1.2.2. Бинарные отношения. Основные определения
- •1.2.4. Эквивалентность и порядок
- •Вопросы для повторения
- •Резюме по теме
- •Тема 1.3. Соответствия и функции
- •1.3.1. Соответствия и их свойства
- •1.3.2. Взаимно однозначные соответствия и мощности множеств
- •1.3.3. Функции и отображения
- •1.3.4. Операции
- •1.3.5. Гомоморфизмы и изоморфизмы
- •Вопросы для повторения
- •Резюме по теме
- •Глава 2. Математическая логика
- •Тема 2.1. Логика высказываний
- •2.1.1. Логические связки
- •2.1.2. Основные схемы логически правильных рассуждений
- •2.2.2. Булева алгебра
- •2.2.3. Эквивалентные преобразования
- •Вопросы для повторения
- •Резюме по теме
- •Тема 2.3. Полнота и замкнутость
- •2.3.1. Функционально полные системы
- •2.3.2. Алгебра Жегалкина и линейные функции
- •2.3.3. Замкнутые классы и монотонные функции
- •2.3.4. Теоремы о функциональной полноте
- •Вопросы для повторения
- •Резюме по теме
- •Тема 2.4. Нечеткая логика
- •2.4.1. Основные понятия теории нечетких множеств
- •2.4.2. Логические операции над нечеткими множествами
- •2.4.3. Свойства логических операций над нечеткими множествами
- •Вопросы для повторения
- •Резюме по теме
- •Тема 2.5. Нечеткие модели управления
- •2.5.1. Нечеткие операторы
- •2.5.2. Нечеткая и лингвистическая переменные
- •2.5.3. Нечеткий логический вывод
- •Вопросы для повторения
- •Резюме по теме
- •Тема 2.6. Логика предикатов
- •2.6.1. Предикаты. Основные понятия
- •2.6.2. Кванторы
- •2.6.3. Выполнимость и истинность
- •2.6.4. Эквивалентные соотношения. Префиксная нормальная форма
- •Вопросы для повторения
- •Резюме по теме
- •Глава 3. Комбинаторика
- •Тема 3.1. Комбинаторные конфигурации
- •3.1.1. Принципы сложения и умножения
- •3.1.2. Перестановки
- •3.1.3. Размещения
- •3.1.4. Сочетания
- •3.2.2. Полиномиальная формула
- •3.2.3. Формула включений и исключений
- •Вопросы для повторения
- •Резюме по теме
- •Глава 4. Теория графов
- •Тема 4.1. Основные понятия и операции на графах
- •4.1.1. Основные понятия
- •4.1.2. Способы задания графов
- •4.1.3. Операции над частями графа. Графы и бинарные отношения
- •Вопросы для повторения
- •Резюме по теме
- •Тема 4.2. Маршруты и деревья
- •4.2.1. Маршруты, пути, цепи, циклы
- •4.2.2. Дерево и лес
- •5.1.2. Способы задания автоматов
- •5.1.3. Взаимосвязь между моделями Мили и Мура
- •Вопросы для повторения
- •Резюме по теме
- •Тема 5.2. Детерминированные конечные автоматы
- •5.2.1.Основные понятия детерминированных конечных автоматов
- •5.2.2. Схема доказательства правильности конечного автомата
- •5.2.3. Произведение автоматов
- •5.3.2. Детерминизация нка
- •Вопросы для повторения
- •Резюме по теме
2.5.1. Нечеткие операторы
Введенные выше операции над нечеткими множествами основаны на использовании операций max и min. В теории нечетких множеств разрабатываются вопросы построения обобщенных, параметризованных операторов пересечения, объединения и дополнения, позволяющих учесть разнообразные смысловые оттенки соответствующих им лингвистических связок естественного языка «и», «или», «не».
Один из подходов
к операторам пересечения и объединения
заключается в их определении при помощи
нечетких
операторов,
т.н. треугольных
норм и конорм.
Следует обратить внимание на то, что
представленные выше варианты вычисления
нечеткого «И» как
min![]() и нечеткого «или» как max
и нечеткого «или» как max
![]() ,
использующиеся как самостоятельно, так
и при введении операций разности,
симметрической разности и дизъюнктивной
суммы – это только один из возможных
вариантов определения данных операций,
веденный основоположником теории
нечетких множеств Л.Заде.
,
использующиеся как самостоятельно, так
и при введении операций разности,
симметрической разности и дизъюнктивной
суммы – это только один из возможных
вариантов определения данных операций,
веденный основоположником теории
нечетких множеств Л.Заде.
Треугольной
нормой
(t-нормой)
называется
двуместная действительная функция T,
отображающая две функции принадлежности
нормальных нечетких множеств
![]() в одну функцию принадлежности нормального
нечеткого множества и удовлетворяющая
следующим условиям:
в одну функцию принадлежности нормального
нечеткого множества и удовлетворяющая
следующим условиям:
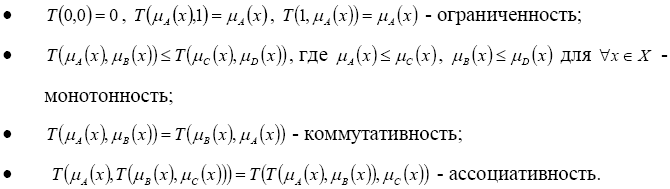
Примерами t -норм являются следующие функции:

Треугольной
конормой
(t-конормой)
называется
двуместная действительная функция T,
отображающая две функции принадлежности
нормальных нечетких множеств
![]() в одну функцию принадлежности нормального
нечеткого множества и удовлетворяющая
следующим условиям:
в одну функцию принадлежности нормального
нечеткого множества и удовлетворяющая
следующим условиям:
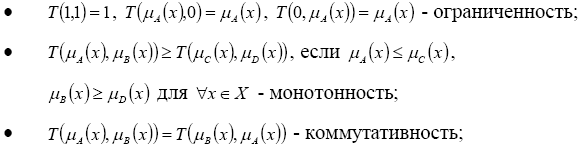
![]()
Примерами t -конорм являются следующие функции:

2.5.2. Нечеткая и лингвистическая переменные
Нечеткая переменная
определяется кортежем параметров
![]() где
где
![]() - название
нечеткой переменной, X
- область
определения нечеткой переменной,
- название
нечеткой переменной, X
- область
определения нечеткой переменной,
![]() -
заданное на X
нечеткое
множество, описывающее возможные
значения нечеткой переменной.
-
заданное на X
нечеткое
множество, описывающее возможные
значения нечеткой переменной.
Пример 1.
Нечеткая переменная,
описывающая скорость движения объекта:
< a
= «приблизительно
нулевая скорость движения объекта»”,
![]() >.
>.
Если областью определения нечеткой переменной является множество действительных чисел Х=R, то такая нечеткая переменная называется действительным нечетким числом.
Лингвистическая
переменная
является
обобщением понятия нечеткой переменной
и определяется кортежем параметров
![]() ,
где:
,
где:
 -
название лингвистической переменной;
-
название лингвистической переменной;T - базовое терм-множество лингвистической переменной, состоящее из множества ее значений (термов), каждое из которых представляет собой название отдельной нечеткой переменной a;
X - область определения нечетких переменных, названия которых составляют терм-множество лингвистической переменной;
G - синтаксическая процедура, позволяющая оперировать элементами терм - множества и генерировать новые термы;
M - семантическая процедура, позволяющая преобразовывать значения лингвистических переменных, полученных процедурой G, в нечеткие переменные, путем формирования соответствующих нечетких множеств.
Пример 2.
Пусть температура воды определяется с помощью понятий «малая температура», «средняя температура», «большая температура». При этом минимальная температура воды равна 0º C, а максимальная – соответственно 100º C . Формализация такого описания может быть проведена при помощи лингвистической переменной , в кортеже которой:
- «температура воды»,
T - «малая температура», «средняя температура», «большая температура»;
X=(0;100);
G - процедура образования новых термов с помощью языковых связок «И», «ИЛИ», а также модификаторов «ОЧЕНЬ», «НЕ», «СЛЕГКА» и т.д. (например, «не очень большая температура»);
M - процедура задания на X=(0;100) нечетких подмножеств, соответствующих понятиям «малая температура», «средняя температура», «большая температура», а также нечетких множеств для термов из G(T) в соответствии с правилами трансляции нечетких связок и модификаторов (A
 соответствует
«И», A
соответствует
«И», A
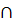 B
соответствует
«ИЛИ»,
B
соответствует
«ИЛИ»,
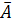 соответствует
«НЕ», CON
(A)=
соответствует
«НЕ», CON
(A)=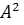 соответствует
«очень», DIL(A)=
соответствует
«очень», DIL(A)=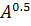 соответствует
«слегка» и т.д.).
соответствует
«слегка» и т.д.).
