Вопросы для обсуждения на форуме

1. Логика высказываний как средство отображения предметной области менеджера.

Список дополнительной литературы:

1. Алехина М.А. Математическая логика: Учеб. пособие. — Пенза: Изд-во Пенз. гос. техн. ун-та, 1996 (80 экз).— 66 с.

2. Москинова Г.И. Дискретная математика. Математика для менеджера в примерах и упражнениях \Г.И. Москинова. – М.: Логос. 2000. – 240с.

3. Судоплатов С.В., Овчинникова Е.В. Элементы дискретной математики: Учебник. — М.: ИНФРА-М, Новосибирск: Изд-во НГТУ, 2002 (20 экз). – 280с.

Семинар №3. Алгебра логики

Цель семинара:

Изучить практическое применение алгебры логики в принятии управленческих решений.

План занятия:

Семинар посвящен темам алгебра логики булева алгебра и полнота и замкнутость. На практическое освоение материала выделяется 2 часа.

Задача 1. Доказать эквивалентность формул:

( &(х₂x₃))~( ) .

Решение.

x1	x2	x3	x2x3	&	x2 x3	x3 x2	&	x1
0 0 0 0 1 1 1 1	0 0 1 1 0 0 1 1	0 1 0 1 0 1 0 1	0 1 1 0 0 1 1 0	0 1 1 0 0 0 0 0	1 1 0 1 1 1 0 1	1 0 1 1 0 0 1 1	1 0 0 1 1 0 0 1	1 0 0 1 1 1 1 1	0 1 1 0 0 0 0 0

Задача 2. Упростим формулы x₂x₃x_{1 2}x₃ и x₁ ₁x₂ _{1 2}x₃ _{1 2}x₃x₄.

Решение.

1. x₂x₃x_{1 2}x₃ = x₃(x₂x_{1 2}) = x₃((x₂x₁)&(x₂ ₂)) = (x₁x₂)x_3.

2. x₁ ₁x₂ _{1 2}x₃ _{1 2}x₃x₄ = x₁ ₁(x₂ _{2 3}x₄) = x₁ ₁(x₂x₃ _{2 3}x₄) = (x₁ ₁)(x₁x₂x₃ _{2 3}х₄) = x₁(x₂x₃)( )x₄ = x₁(x₂х₃( ))(x₂x₃x₄) = x₁x₂x₃x_4.

Задача 3. Пусть функция f(x₁, x₂, x₃) задана таблицей истинности.

x1	x2	x3	f
0 0 0 0 1 1 1 1	0 1 1 1 0 0 1 1	0 1 0 1 0 1 0 1	0 0 1 0 1 0 0 1

Запишем ее в виде СДНФ.

Решение.

Наборов, на которых функция равна 1, три: (0, 1, 0), (1, 0, 0) и (1, 1, 1), поэтому f(x₁, x₂, x₃) = x₁⁰ & x₂¹ & x₃⁰ x₁¹ & x₂⁰ & x₃⁰ x₁¹&x₂¹ & x₃¹=

= &x₂& x₁& & x₁&x₂&x_3.

Задача 4. Пусть f(x₁, x₂, x₃) = x₁ (x₂ (x₃ ~ x₁)). Представить ее в виде СКНФ.

Решение.

Для этого получим таблицу истинности.

x1	x2	x3	x3~x1	x 2 (x3~x1)	f
0 0 0 0 1 1 1 1	0 0 1 1 0 0 1 1	0 1 0 1 0 1 0 1	1 0 1 0 0 1 0 1	1 1 1 0 1 1 0 1	1 1 1 1 1 1 0 1

Функция равна нулю только на наборе (1, 1, 0), поэтому

f(x₁ x₂ x₃)=x₁ x₂ x₃ =x₁⁰x₂⁰x₃¹=   x₃.

Задача 5. Упростить булевы формулы:

1. (х₁,х₂,х₃)= ;

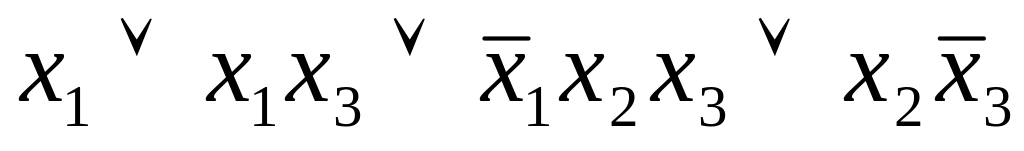2. (x,y,z)=

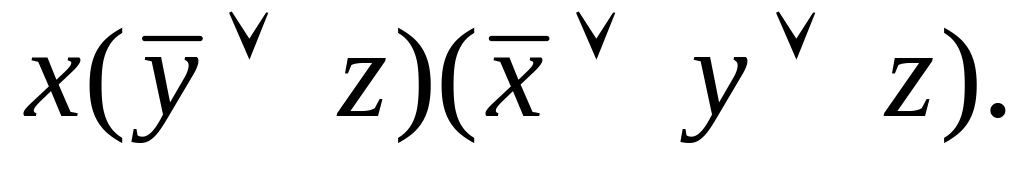
Решение.

a

(4 24)

) (х₁,х₂,х₃)= =

б)(x,y,z)= =

Задача 6. Представить булеву формулу в базисе { } и ( }.

Решение.

Представим формулу базиса {} в базисах {} и {}, последовательно используя правила де Моргана, а также правило двойного отрицания:

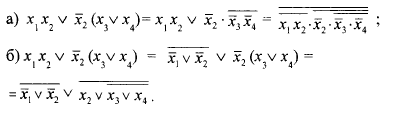
Булев базис {  } в некотором смысле "избыточен" - при удалении из него операции & или v функциональная полнота полученных систем {} и {} сохраняется. Однако в представлении { &, , } логические функции выражаются более простыми формулами, как это видно из примера. За неизбыточность базисов операций приходится платить избыточностью формул: каждая замена одной операции на другую вносит в формулу лишние отрицания.

Задача 7. Запишем с неопределенными коэффициентами полином Жегалкина для функции трех переменных f(x₁, x₂, x₃) = (01101001) = а₀ а₁х₁ а₂х₂ а₃х₃ b₁x₁x₂ b₂x₂x₃  b₃x₁x₃  cx₁x₂x₃. Затем находим коэффициенты, используя значения функции на всех наборах. На наборе (0, 0, 0) f(0, 0, 0) = 0, с другой стороны, подставив этот набор в полином, получим f(0, 0, 0) = а₀, отсюда а₀ = 0. f(0, 0, 1) = 1, подставив набор (0, 0, 1) в полином, получим: f(0, 0, 1) = а₀ а₃, т.к. а₀ = 0, отсюда а₃ = 1. Аналогично, f(0, 1, 0) = 1 = а₂, f(0, 1, 1) = 0 = а₂ а₃ b₂ = b₂ = 0; а₁ = 1; 0 = а₁ а₃ b₃ = b₃ = 0; 0 = а₁  а₂ b₁ = b₁ = 0; 1 = 1 1 1 c; c = 0; f(x₁, x₂, x₃) = x₁ x₂ x₃.