
- •Произвольная призмa
- •Шар и сфера
- •Формулы сокращённого умножения
- •Теорема Виета
- •Теорема синусов
- •Теорема косинусов
- •Радианная и градусная меры углов
- •Особые решения
- •Квадраты и кубы натуральных чисел
- •Степени чисел 2 и 3
- •Длина вектора а
- •Координаты вектора
- •Действительные числа
- •Длина биссектрисы
- •Уравнение касательной к графику функции f(X) в точке х0
- •Логарифмы и их свойства
Sбок =
Pсеч . l,
где l
- боковое ребро
V = Sсеч.
l V = Sсеч.
H Sполн
= Sбок + 2Sосн
Прямая призма
Sбок = P
H Sполн
= Sбок + 2Sосн
V = Sосн.
H
Прямоугольный параллелепипед
Sбок
= P H V = abc
Sпол
= 2(ab + bc + ac) d2
= a2
+ b2
+ c2
Куб
V = a3
d = а Произвольная
пирамида
Sполн = Sбок
+ Sосн
V =
Правильная пирамида
28Произвольная призмa
![]() Sполн =
6а2
Sполн =
6а2![]() Sосн
. H
Sосн
. H
Квадрат
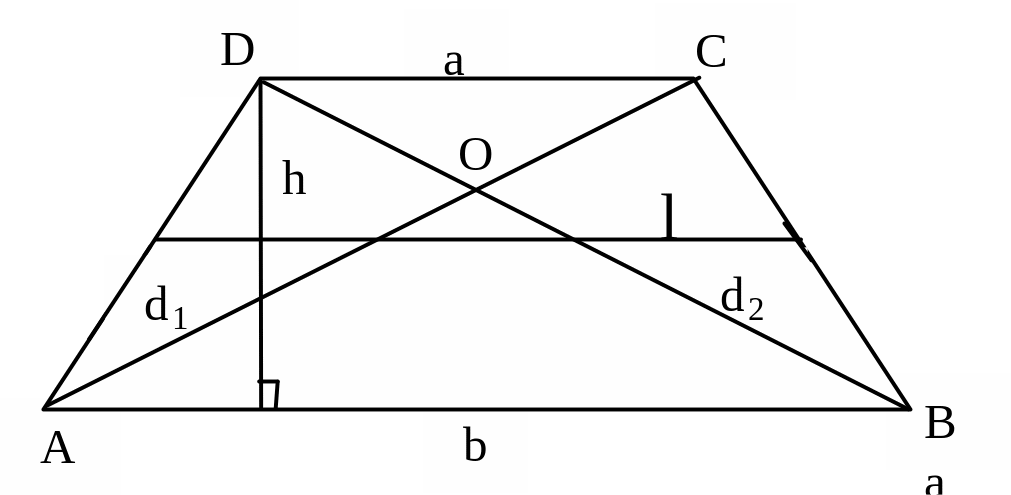
Трапеция
l =
S = lh =
O –
угол между диагоналями
l –
средняя линия трапеции


![]()
![]() ,где
,где
Усечённый конус
Sбок =
l ( R
+ r )
Sполн
= Sбок + S1
+ S2
S1
= π R2
S2
= π r2
где Н – высота,
l – образующая,
R и r –
радиусы оснований
где R
– радиус шара,
S – площадь
сферической поверхности,
V – объём,
D – диаметр.
Шар и сфера

а2 - b2 = (а + b)
(а - b)
(а + b)2 = а2 +
2аb + b2
(а - b)2 = а2 -
2аb + b2
(а + b)3 = а3 +
3а2b+ 3аb2
+ b3
(а - b)3 = а3 -
3а2b+ 3аb2
- b3
а3 + b3 = (а + b)
(а2 – аb + b2)
а3 - b3 = (а - b)
(а2 + аb + b2)
х2 + pх + q
= 0,
х1
. х2
= q
х1 +
х2 =
- р,
где
х1 и
х2 –
корни
приведенного квадратного уравнения Разложение
квадратного трёхчлена на множители
ах2 + bх + с
= а (х - х1).(х - х2)
,где
х1 и
х2 – корни
квадратного трёхчлена.
Если D=0,
то
ах2+вх+с = а .
(х - х1)2
Формулы сокращённого умножения
Теорема Виета
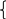
Площадь круга
Длина окружности
Соотношения между
сторонами и углами в прямоугольном
треугольнике
Теорема синусов
![]()
Теорема косинусов

![]()
![]()

![]()
Таблица первообразных
Функция f(x)
Первообразная F(x)
C
Cx
xп
ex
ex
ax
ax/lna
cos(ax + b)
1/asin(ax
+ b)
sin(ax + b)
- 1/a
cos(ax + b)
sin x
- cos x
cos x
sin x
1/cos2
x
tg x
1/ sin2
x
- ctg x
2
1/х2
-1/х
![]()
![]()
![]()

![]()
Соотношение между тригонометрическими
функциями одного и того же угла
Формулы сложения
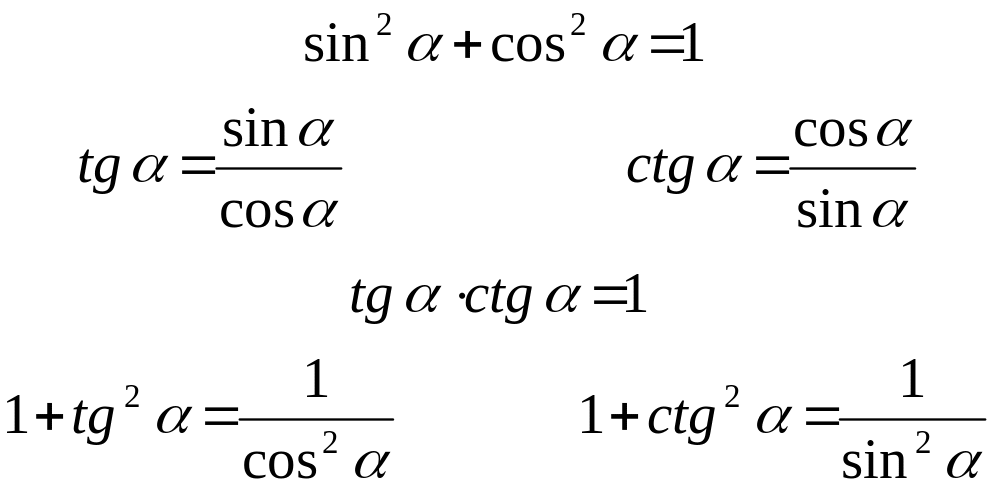

Формулы половинного аргумента
Универсальные тригонометрические
подстановки
11

Иррациональное неравенство
Логарифмическое
неравенство
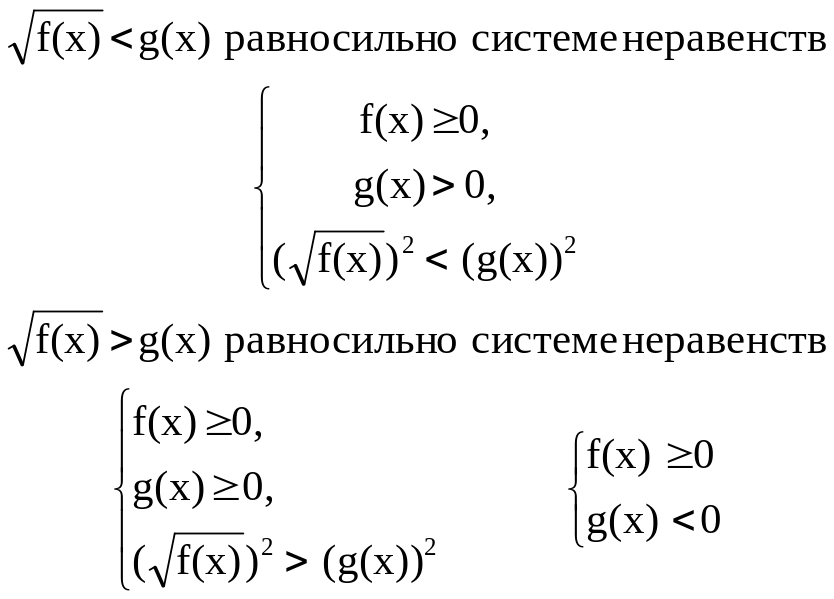 Показательное
неравенство
Показательное
неравенство![]()
![]()
Арифметическая прогрессия
an+1
= an
+ d опред.
арифм. прогр.
an
= a1 + (n
– 1) d – форм.
п-го члена
арифметической
прогрессии.
Sn =
сумма п – первых
членов арифм. прогр.
Геометрическая
прогрессия
bn+1
= bn
q определение
геом. прогр.
bn
= b1 qn-1
формула п – го
члена геом. прогр.
Sn
=
сумма п – первых
членов геом. прогр.
bn
=
S =
18![]() -
характерист.
свойство.
-
характерист.
свойство.![]() n
-
n
-![]() -
-
![]() - характерист.
свойство
- характерист.
свойство![]() - сумма бесконечно
убывающей геометрической прогрессии.
- сумма бесконечно
убывающей геометрической прогрессии.![]()
