17. Крывізна і кручэнне.

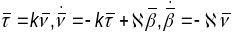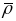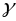
З фармальнага пункта гледжання, крывізна k гэта адпаведны каэффіцыент у формулах прамых: . З іншага пункта гледжання, крывізна k есць … хуткасць змянення кіроўнага вектара датычнай прамой, ці што тое самае імгненнае паскарэнне параметра крывой 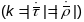, а кручэнне 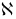з дакладнасцю да знака – імгенная хуткасць змянення кіроўнага вектара бінармалі .

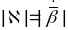Вынік:

1. Крывізна k - неадмоўная велічыня;

2. Кручэнне 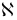- можа прымаць як адмоўнае, так і дадатнае і нулявое кручэнне у пункце крывой: , , .

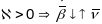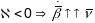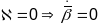Тэарэма (геаметрычны сэнс k і 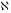): Няхай – (бі)рэгулярная элементарная крывая класа (С³) С², Р – адвольны яе пункт, Q – некаторы яе пункт блізкі да Р, р, q – (бінармалі) датычныя крывой у пункце Р і Q. 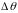– вугал паміж р і q, 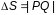- даўжыня дугі РQ, k(Р)= ,

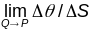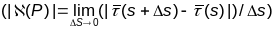
Адкладваюць 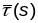, , 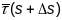атрымаем раўнабокі трохвугольнік.

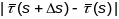
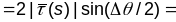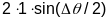= . Вяртаючыся да k(Р) працягваем:

.

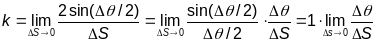Другая формула для 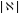даказваецца аналагічна:

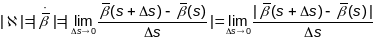
Вынік: Такім чынам, крывізна і кручэнне – гэта геаметрычныя варыянты, якая прадстаўляюць сабой імгненны вугал хуткасці датычнай прамой і бінармалі адпаведна.

20. Крывізна і кручэнне акружнасці, гарфіка функцыі, шрубавай лініі.

Пр.1:Вылічыць крывіз. і кручэн. акружнасці радыўса R.

Рашэнне: (1 спосаб) (на основе геаметрычнага сэнсу k і )

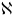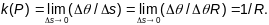
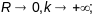
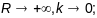
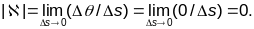
Адказ: , .

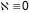(2 спосаб) Параметрызуем акружнасць:

, ,

, ,

,

, ,

,

, .

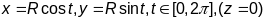
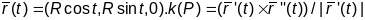
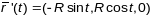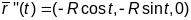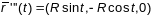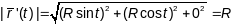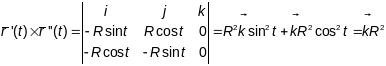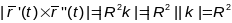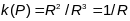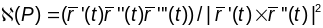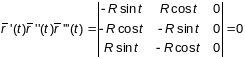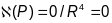Прыклад 2: Вылічыць крывізну і кручэнне графіка функцыі .

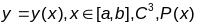Рашэнне: Параметрызуем гарфік функцыі: .

, , , ,

, .

, .

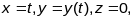
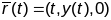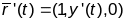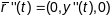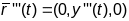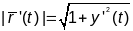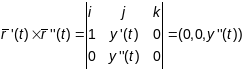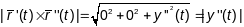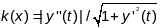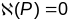Вынік: У пункце перагібу графіка функцыі 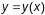плоскай крывой, крывізна ці роўна нулю, ці не існуе.

Прыклад 3: Знайсці крывізну шрубавай лініі .

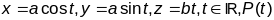Рашэнне: .

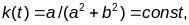
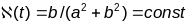21. Крывая нулявой крывізны. Пункты спрамлення (выпроствання).

Тэарэма: Крывая класа С² нулявой крывізны есць прамая, ці яе частка; адваротнае таксама праўдзіва.

Доказ: (1) Няхай

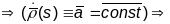
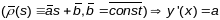
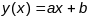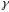( - прамая ці яе частка)

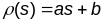.Паколькі лінейная адносна параметра s, задае прамую. (2) Усе лагічныя пераходы адварочваюцца.

Азначэнне: Пункт крывой , у якім крывізна k=0 называецца пунктам выпроствання.

Заўвага: Пункты выпроствання могуць цалкам запаўняць усю крывую (прамая ці яе частка); зусім адсутнічаць на крывой (акружнасць, шрубава лінія); ляжаць на ей ізаляваня.

Сцверджанне: Пункты выпроствання гладкай крывой класа С² характарызуюць роўнасці: .

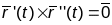Паколькі 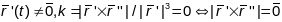. Адсюль атрымалі сцверджанне аб геаметрычным сэнсе паняцця бірэгулярнай крывой.

Сцверджанне: Гладкая крывая класа С² з’яўляецца бірэгілярнай тады і толькі тады, калі яна не мае пунктаў выпроствання .

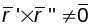22. Крывая нулявога кручэння. Пункты сплашчэння.

Тэарэма: Гладкая крывая класа С³ нулявога кручэння з’яўляецца плоскай; адворотнае таксама праўдзіва.

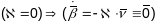
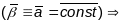
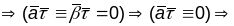
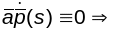
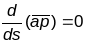
Доказ: (1) Няхай 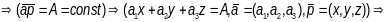( 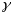- плоская крывая), таму што каардынаты адвольнага яе пункта 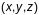задавальняюць раўнанню адной і той жа плоскасці. (2) (Няхай - плоская крывая) 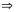(яе судаты-кальная плоскасць П супадае з плоскасцю крывой ) ( ) ( ) ( ) ( ).

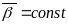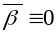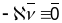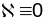Азн.: пункт крывой, у якім кручэнне роўна нулю, называецца пунктам сплашчэння.

Заўвага: пункты сплашчэння могут цалкам запаўняць крывую (плоская крывая), могуць адсутнічаць на крывой (шрубавая лінія) і могуць ляжаць на ей ізалявана.

Сцверджанне: для знаходжання пунктаў сплашчэння крывой (бірэгулярнай класа 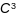) выкарыстоўваць іх характарыстычную уласцівасць 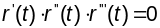(змешана-га здабытку)