57

2. Элементарная крывая. Агульныя крывыя. Простыя крывыя.

Азн.: тапалагічным ці гамеаморфным адлюстраваннем фігу-ры на фігуру нызываецца узаемаанназначнае і ўзаемна-непарыйнае адлюстраванне першай з іх на другую. Абазначаецца ~ .

Азн.: элементарнай крывой (э.к.) у прасторы наз. го-меаморфны вобраз у гэтай прасторы элементарнага прамежка прамой, г.зн. адрэзка, адрэзка без аднаго ці двух канцоў, адкрытага ці замкнутага промня, усей прамой. Абазначаецца .

Заўвага: паколькі элементарныя прамежкі прамой гомеаморфныя адпаведна прамежку лікавай прамой, можна казаць, што э.к. гамеаморфны вобраз прамежка лікавай прамой.

Сярод э.к. есць замкнутая (адкрытая), паўзамкнутая (паўадкрытая) дугі. Бясконцыя ў адзін бок і ў два бакі.

Азн.: агульная крывая (а.к.) – фігура ў прасторы, якую можна пакрыць канечным ці злічоным мноствам элементарных крывых. Абазначаецца .

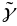Пакрыццем мн-ва Х наз. адвольная сукупнасць яго пад-мн-ваў ( ), такая, што ( 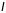- індэкснае мн-ва).

Бясконцае мноства называецца злічоным, калі яго элементы можна пранумераваць натуральнымі лікамі.

Сцверджанне1: калі пункт , тады , якая ляжыць ў .

Вынік: вывученне агульных крывых у малым зводзіцца да вывучэння э.к.

Тапалагічна звычайны пункт а.к. – пункт, які мае наваколле ў прасторы, перасячэнне якога з гэтай крывой э.к. пункт а.к. называецца тапалагічна асаблівым, калі ен не з’яўляецца тапалагічна звычайным.

Простая крывая (п.к.) – а.к., якая задавальняе двум умовам:

1. З’яўляецца звязнай (гэта значыць складаецца з аднаго куска).

2. Не мае тапалагічна асаблівых пунктаў.

Заўвага: 1. Часта крывыя называюць лініямі.

2. Крывая, якая цалкам ляжыць у плоскасці называецца плоской.

5. Гадкая (рэгулярная) элементарная крывая.

Элементарная крывая Υ называецца э.к. класа С^к (к=0,1,2,…), калі яна дапускае параметрызацыю класа С^к. Крывыя класа С⁰ называюцца непарыўнымі, класа С^к (к>=1) называюцца к-разоў непарыўна дыфферэнцаваныя.

Параметрызацыя 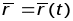, 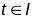называецца гладкай (рэгулярнай) класа С^к (к=0,1,2,…), калі выконваюцца умовы:

1. .

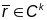2. , .

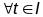Э.к. называецца гладкай (рэгулярнай) класа С^к (к=0,1,2,…), калі яня валодае гладкой (рэгулярнай) параметрызацыяй класа С^к.

Заўвага: рэгулярная крывая можа мець і нягладкую параметрызацыю.

10. Датычная прамая крывой.

Азн.: датычнай прамой крывой у яе пункце Р наз. лімітавае становішча яе сякучай, што праходзіць праз Р і нейкі іншы пункт Q крывой , пры умове, што Q неабмежавана набліжаецца да Р, рухаючыся па кр. .

Тэарэма:

1. (Існаванне) Усякая рэгулярная кр. 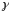у кожным сваім п. Р мае датычную прамую Т і прычым адзіную.

2. (адзінасць) Калі 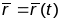, 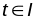- адвольная дапушчальная параметрызацыя гладкай кр. , тады век-тарнае параметрычнае раўнанне яе датычнай пра-мой Т у яе п. Р можна запісаць у выглядзе: , .

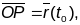
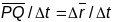Доказ: 1. Калі 0 – пачатак сістэмы каардынат, тады Вектар кіроўны вектар сечнай прамой PQ. Вектар - кіроўны вектар сечнай PQ. Калі на , 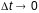і паколькі 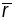- галдкая параметрызацыя крывой існуе і адрозніваецца ад 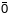. . 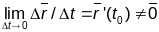Відавочна прамая Т, якая будзе праходзіць праз Р у напрамку гэтага вектара 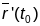і будзе лімітавым становішчам пераменнай сякучай PQ. 2. Няхай 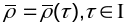- іншая далучаная пара-метрызацыя крывой 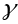эквшвалентна яе параметрызацыі . Г.зн. 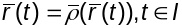. 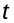Дыфферэнцыруя па будзем мець . Паколькі якабіан зменнай параметра 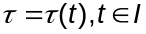адрозніваецца ад , атрымалі, што 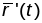і у адным і тым жа пункце Р каленіарныя. Такім чаным, у гэтым пункце яны вызначаюць адну і тую ж прамую Т, для якой з’яўляюцца кіроўнымі вектарамі.

3. (канструк-тыўнасць) Вывад раўнання: Нахай 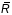- радыўс-вектар бя-гучага пункта М датычнай прамой Т. , .

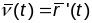Вынік: Калі - адвольная дапушчальная параметрызацыя гладкай крывой , тады вектар есць кіроўны вектар датычнай прамой крывой у яе пункце с вектарам хуткасці параметра у адвольным пункце.