О г л а в л е н и е
Интегральное исчисление функции одной переменной………………………………5
1. Первообразная. Неопределенный интеграл………………………………….…….5
2. Таблица основных интегралов………………………………………………….…..5
3. Основные свойства неопределенного интеграла………………………………….6
4. Основные методы интегрирования………………………………………..………..7
4.1. Непосредственное интегрирование…………………………………….………7
4.2 Замена переменной………………………………………………………………8
4.3 Интегрирование по частям…………………………………….………………10
5. Интегралы специального вида……………………………………………………12
Задача о вычислении площади криволинейной трапеции………………………17
7. Определенный интеграл. Формула Ньютона-Лейбница……………….……….19
8. Основные свойства определенного интеграла………………………….……….20
9. Основные методы вычисления определенного интеграла…………….………..22
9.1. Непосредственное применение формулы Ньютона-Лейбница….……….22
9.2. Замена переменной в определенном интеграле…………………..……….23
9.3 Интегрирование по частям для определенного интеграла………..……….25
10. Вычисление площадей фигур с помощью определенного интеграла…..………25
11. Несобственные интегралы…………………………………………………..…….28
Примеры выполнения контрольных заданий по разделу « Интегральное исчисление функции одной переменной »……………………………………………29 Интегральное исчисление функций одной переменной
1. Первообразная. Неопределенный интеграл
Основная задача дифференциального исчисления состоит в нахождении дифференциала данной функции или ее производной. Интегральное исчисление решает обратную задачу: для данной функции f(x) найти такую функцию F(x), производная которой равна f(x). Например, для функции f(x)=
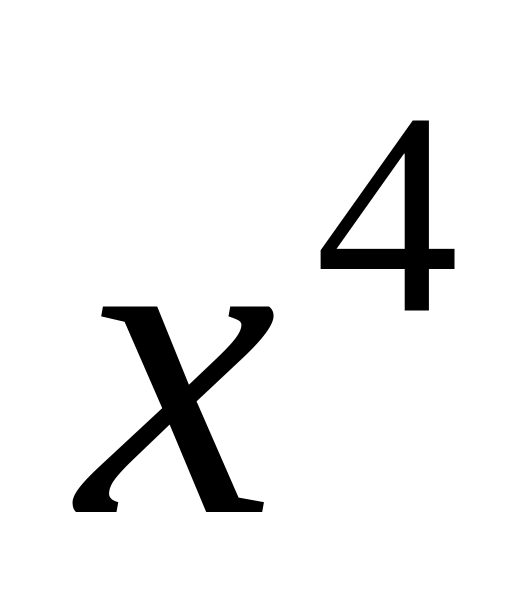этому условию удовлетворяет функция
F(x)=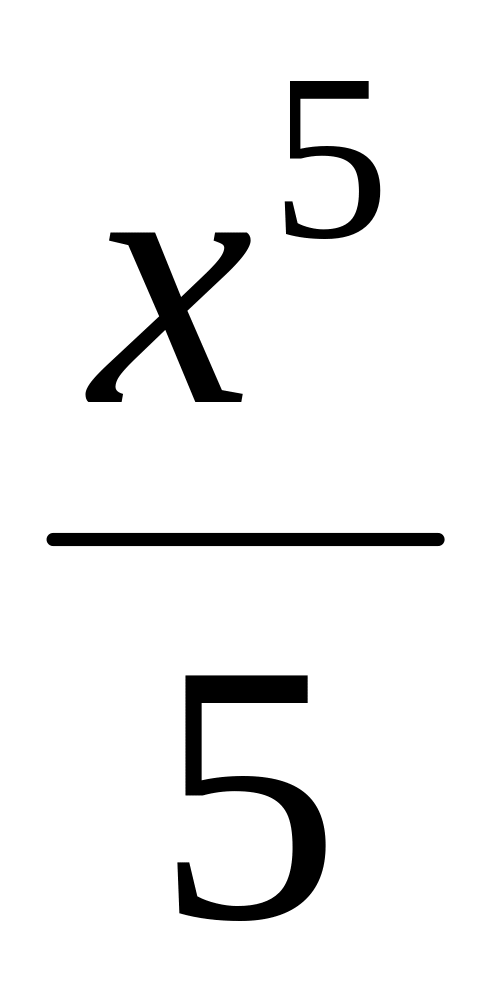
,так как
.
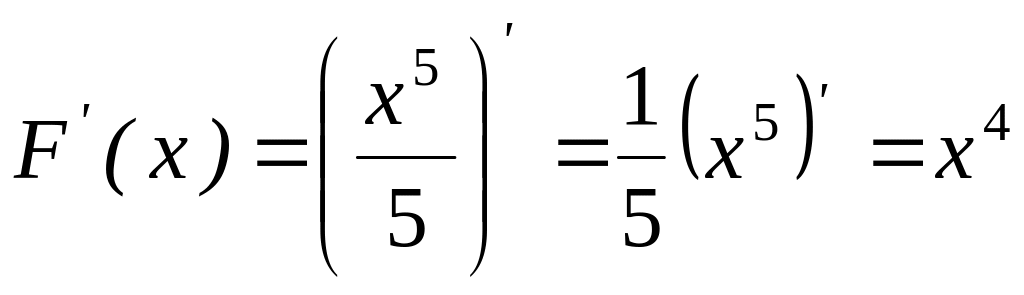Функция F(x)
называется первообразной для функции
f(x),
если
.
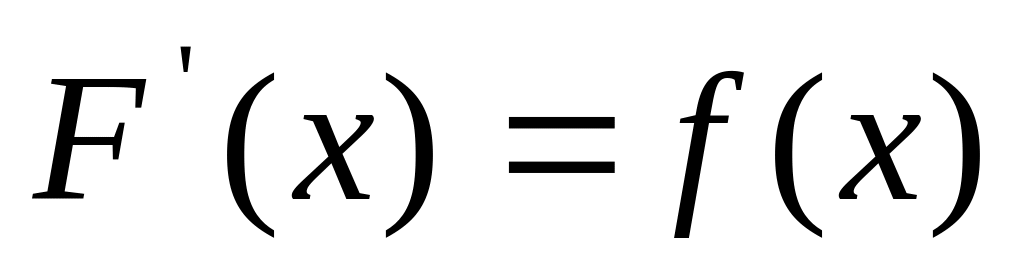Следовательно,
функция
является первообразной для функции
.
Однако, она не является единственной
первообразной для
.
Ими являются функции
и вообще
,
где С –
произвольная постоянная.
Оказывается, что все первообразные для любой функции f(x) даются
формулой F(x)+C, где
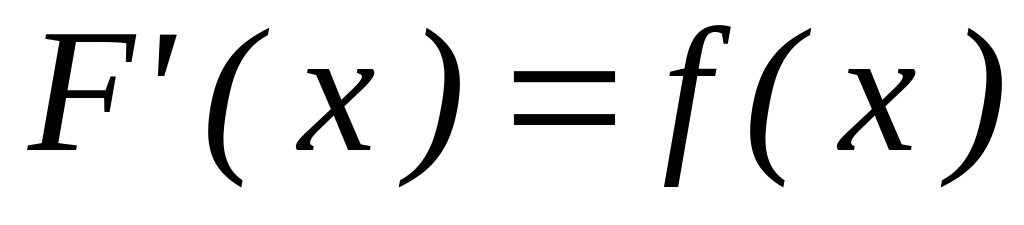и С
– произвольная постоянная.
Совокупность
всех первообразных для непрерывной
функции f(x)
называется неопределенным интегралом
и обозначается
,
где функция f(x)
– подынтегральная функция, f(x)dx
– подынтегральное выражение, dx
– дифференциал аргумента. Таким образом,
если F(x)
– какая-либо
первообразная
для f(x),
то
.
Например,
.
Процесс нахождения неопределенного
интеграла называется интегрированием
этой функции.
Из определения неопределенного интеграла следует, что каждой формуле дифференциального исчисления F’(x)=f(x) соответствует формула в интегральном исчислении.
2. Таблица основных интегралов
Следующие формулы интегрального исчисления получены из таблицы основных производных с добавлением к ним наиболее часто встречающихся интегралов. Заметим, что правильность всех этих формул проверяется путем вычисления производных от их правых частей.
Интегралы из этой таблицы в дальнейшем будем называть табличными интегралами.
3. Основные свойства неопределенного интеграла
Из определения неопределенного интеграла вытекают следующие свойства:
Важную роль при вычислении неопределенного интеграла играют следующие
его свойства, которые доказываются с помощью соответствующих свойств
производной:
5)
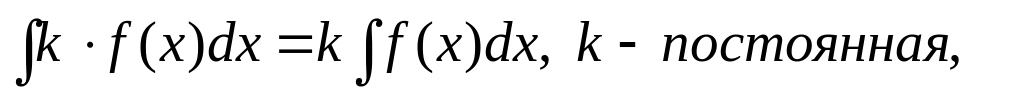
4. Основные методы интегрирования
4.1. Непосредственное интегрирование.
Метод заключается в применении свойств 5 и 6 с использованием таблицы основных интегралов.
Пример 1
(
по таблице основных интегралов)=
=
Пример 2
Пример 3
Пример 4
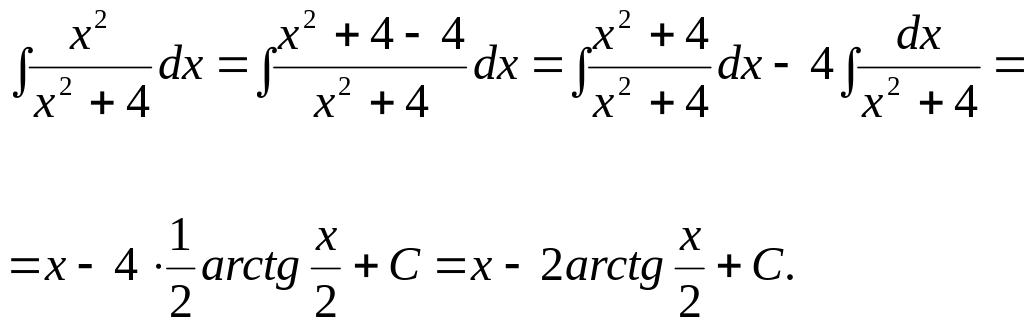
Пример 5
(по
формуле тригонометрии)=
=
. Замена переменной
Метод заключается в переходе к новому аргументу интегрирования путем преобразования подынтегрального выражения по некоторой формуле.
При этом говорят, что в интеграле слева сделана замена переменной (подстанов-
ка по формуле
После вычисления
интеграла справа необходимо в ответе
вернуться снова к аргументу x
, выразив t
в формуле
через x
.
Замечание. Часто при замене переменной удобно использовать подстановку
вида
,
при этом
