28) После сбора данных осуществляется их регрессионный анализ, который включает три этапа:

1) определение вида функции (уравнения регрессии);

2) определение тесноты связи между переменными;

3) установление числового значения параметров уравнения регрессии.

На первом этапе определяется форма связи исследуемых показателей или уравнение регрессии. Функциональная зависимость определяется следующим образом: предположим, что линия регрессии переменной, которую мы обозначим , от  переменной Х имеет вид: = а0 + а1Х+- это простейший вид зависимости между двумя показателями – линейная зависимость. Здесь - результативный показатель, а0 и а1- постоянные коэффициенты, Х – фактор, - добавочный коэффициент, при учете которого никогда не может попасть на линию регрессии, т.е. Х.

Это уравнение можно использовать как предсказывающее уравнение, подстановка в него значения Х позволяет предсказать истинное среднее значение У для этого Х.

Проверка линейной зависимости может быть проведена путем сопоставления по собранным данным вариации результативного и факторного признаков. Любую форму зависимости можно проверить графическим путем, отмечая каждое наблюдение точкой в прямоугольной системе координат. По оси ординат откладываются значения У, а по оси абсцисс – значение Х.

Вторым этапом проверяется теснота связи выбранных показателей, т.е. насколько полно выбраны факторные признаки, как велико влияние неучтенных факторов. Поэтому оценка параметров регресси и обычно сопровождается расчетом такой дополнительной характеристики, как коэффициент корреляции, который представляет собой эмпирическую меру линейной зависимости между Х и Y:

ry,x= (,

где - среднеарифметическое значение результативных признаков; - среднеарифметическое значение факторов; n- количество выборочных наблюдений; - среднее квадратическое отклонение результирующего и факторного признаков.

Среднее квадратическое отклонение фактора рассчитывается по формуле:

Среднее квадратическое отклонение значений результирующего признака рассчитывается по формуле:

Величина коэффициента корреляции лежит между (-1;1). Чем выше значение коэффициента корреляции, тем теснее связь между переменными и тем точнее будет прогноз, произведенный на основе полученного уравнения регрессии. Если коэффициент корреляции равен +1, то связь между показателями выражается в прямой зависимости, т.е. при увеличении одного показателя увеличивается и второй и наоборот. Если же коэффициент корреляции равен –1, то связь между двумя показателями выражается в обратной зависимости, т.е. при увеличении одного показателя другой уменьшается, и наоборот.

О тесноте связи можно судить по значению коэффициента корреляции, используя шкалу Чеддока:

Показатели тесноты связи 0,1-0,3 0,3-0,5 0,5-0,7 0,7-0,9 0,9-0,99 Характеристика силы связи слабая умеренная заметная высокая весьма высокая Завершающим этапом является определение численных значений постоянных коэффициент ов уравнения регрессии (а0 и а1). Эти коэффициенты находятся в результате решения системы уравнений. Систему можно получить с помощью метода наименьших квадратов. Метод наименьших квадратов позволяет из бесчисленного множества прямых линий на плоскости выбрать одну, наилучшим образом соответствующую исходным данным.

Этот метод обладает определенными свойствами: пусть мы имеем множество из n наблюдений (Х1,Y1), (Х2,Y2)…(Хn, Yn). Тогда уравнение = а0 + а1Х+ можно записать в виде:

i = а0 + а1Хi+i, где i=1,2…n.

Следовательно, сумма квадратов отклонений фактических значений от расчетных равна:

S=i2=2.

Будем подбирать значения оценок а0 и а1 так, чтобы их подстановка в уравнение давало наименьшее значение S, т.е. 2= Smin

Определим а0 и а1 дифференцируя уравнение S=i2=2, сначала по а0, затем по а1 и приравняем результаты к нулю. Тогда получим:

na0 + a1

Эти уравнения представляют собой систему нормальных уравнений. Отсюда находим коэффициенты регрессионной функции:

а1==

Решение системы уравнений относительно а0: а0=Y-a1X. С помощью подстановки этого уравнения в уравнение i = а0 + а1Хi+i получим оцениваемое уравнение регрессии Yi= Y+a1X.

Для практического использования регрессионных моделей важно установить, насколько точно могут быть рассчитаны значения исследуемого показателя по заданным значениям факторов. Для оценки точности уравнений регрессии на практике используют ряд показателей: коэффициент множественной корреляции (детерминации), критерий Фишера, остаточная дисперсия, критерий Стьюдента и др.1

Следует отметить, регрессионные приемы анализа и прогнозирования не вскрывают специфические причины изучаемых явлений, а только дают возможность определить количественную величину связей между ними. Причины могут быть вскрыты только при тщательном изучении технической, технологической и организационной сторон процесса производства и экономических отношений.

Рассмотрим пример прогноза на основе испол ьзования корреляционно-регрессионного анализа. Оценить зависимость между среднедушевыми доходами населения и потреблением мяса и мясопродуктов на душу населения в регионе за 11 лет. (исходные данные представлены в таблице 3.1). Сделать прогноз потребления мяса и мясопродуктов на душу населения при условии, что среднедушевые доходы в следующем году увеличатся на 10%.

Таблица 3.1 – Исходные данные по региону

Год Среднедушевые

денежные доходы населения (в месяц в руб.,

до пятого г. – тыс. руб.) Потребление мяса и мясопродуктов на душу населения в год, кг 1 0,248 59 2 536 51 3 834 51 4 1016 50 5 1163 46 6 1908 45 7 2500 48 8 3396 53 9 4689 59 10 6205 64 11 7552 69 Рассмотрим решение задачи средствами Excel.

1. Заносим статистические данные на лист Excel.

2. Оценим тесноту связи между среднедушевыми доходами населения и потреблением мяса и мясопродуктов на душу населения. Для этого выберем надстройку ВСТАВКА ? ФУНКЦИЯ ? КОРРЕЛ ? ОК.

В открывшемся диалоговом окне КОРРЕЛ зададим несколько параметров: в поле Массив 1 укажем диапазон ячеек В1:В11, в поле Массив 2 - диапазон ячеек А1:А11.После того как все необходимые параметры заданы, щёлкните по кнопке ОК – Excel выводит на лист коэффициент корреляции. Для данных исходных данных он равен 0,749, это означает, что связь между показателями высокая. Следовательно, можно перейти к регрессионному анализу.

3. Составим уравнение регрессионной зависимости. Для этого выберем надстройку СЕРВИС ?АНАЛИЗ ДАННЫХ?РЕГРЕССИЯ?ОК. В открывшемся диалоговом окне РЕГРЕССИЯ зададим несколько параметров:

* в поле Входной интервал Y укажем диапазон с входными данными В1:В11;

* в поле Входной интервал X укажем диапазон с входными данными А1:А11;

* флажок Метки устанавливают, если первая строка исходного диапазона содержит название полей – в нашем случае – нет.

* флажок Константа – ноль устанавливается, если требуется, чтобы линия регрессии проходила через начало координат – в нашем случае – нет;

* флажок Уровень надежности устанавливают с целью изменить уровень значимости ? (Excel автоматически задает надежность ?=0,95, что соответствует уровню значимости ?=1 – ?=0,05). В случае ??0,05 установите флажок и в соседнем поле введите надежность 1 – ?. В нашем случае этого не требуется;

* с помощью переключателя Параметры вывода, определим, куда должны быть помещены выходные данные – установим переключатель в позицию Выходной интервал, в соответствующем поле укажем ячейку C13.

* флажок Остатки устанавливают, если требуется получить разность между фактическими и теоретическими значениями Y – не устанавливаем флажок;

* флажок График остатков устанавливают, если требуется получить диаграмму остатков для каждого значения X – не устанавливаем флажок;

* флажок Стандартные остатки устанавливают, если требуется получить нормальные остатки (каждый из остатков делится на стандартное отклонение остатков) – не устанавливаем флажок;

* флажок График подбора устанавливают, если требуется получить точечную диаграмму входных значений Y и значений Y, вычисленных по уравнению регрессии относительно переменной X – устанавливаем флажок;

* флажок График нормальной вероятности устанавливают, если требуется получить график нормального распределения персентиля выборки и исходных значений Y – не устанавливаем флажок.

После того как все необходимые параметры заданы, щёлкаем по кнопке ОК – Excel выводит параметры уравнения регрессии.

4. Для того, чтобы уравнение появилось на диаграмме необходимо правой кнопкой мыши нажать на одно из значений графика Прогноза. Далее в диалоговом окне выбрать Добавить линию тренда.

5. В диалоговом окне Линия тренда выберите тип предполагаемой зависимости, например, предположим, что зависимость линейная. Далее выберите команду Параметры, в появившемся диалоговом окне отметьте флажок на команде Показать уравнение на диаграмме.

С помощью полученного уравнения регрессии У= 0,0023х + 47,8 получим прогнозное значение У = 0,0023*7552*1,1 + 47,8 = 66,9 кг – прогнозное значение потребления мяса и мясопродуктов на душу населения в год в регионе, при условии, что среднедушевые доходы увеличатся в следующем году на 10%.

Краткие выводы по теме

Исследование зависимостей и взаимосвязей между объективно существующими явлениями и процессами играет большую роль в экономике. Оно дает возможность глубже понять сложный механизм причинно-следственных отношений между явлениями. Для исследования интенсивности, вида и формы зависимостей широко применяется корреляционно-регрессионный анализ, который является методическим инструментарием при решении задач прогнозирования и планирования.

Понятия «корреляция» и «регрессия» тесно связаны между собой. В корреляционном анализе оценивается сила связи, а в регрессионном анализе исследуется ее форма. Корреляция в широком смысле объединяет корреляцию в узком смысле и регрессию.

Исследование корреляционных связей называют корреляционным анализом, а исследование односторонних стохастических зависимостей – регрессионным анализом.

29) Коэффициент ранговой корреляции Спирмена - это непараметрический метод, который используется с целью статистического изучения связи между явлениями. В этом случае определяется фактическая степень параллелизма между двумя количественными рядами изучаемых признаков и дается оценка тесноты установленной связи с помощью количественно выраженного коэффициента.

Практический расчет коэффициента ранговой корреляции Спирмена включает следующие этапы:

1) Сопоставать каждому из признаков их порядковый номер (ранг) по возрастанию (или убыванию).

2) Определить разности рангов каждой пары сопоставляемых значений.

3) Возвести в квадрат каждую разность и суммировать полученные результаты.

4) Вычислить коэффициент корреляции рангов по формуле:.

где   - сумма квадратов разностей рангов, а   - число парных наблюдений.

При использовании коэффициента ранговой корреляции условно оценивают тесноту связи между признаками, считая значения коэффициента равные 0,3 и менее, показателями слабой тесноты связи; значения более 0,4, но менее 0,7 - показателями умеренной тесноты связи, а значения 0,7 и более - показателями высокой тесноты связи.

Мощность коэффициента ранговой корреляции Спирмена несколько уступает мощности параметрического коэффициента корреляции.

Коэффицент ранговой корреляции целесообразно применять при наличии небольшого количества наблюдений. Данный метод может быть использован не только для количественно выраженных данных (пример 1), но также и в случаях, когда регистрируемые значения определяются описательными признаками различной интенсивности (пример 2).

30) На основе хи-квадрата принято также оценивать показатели степени тесноты связи - коэффициенты взаимной сопряженности К.Пирсона и А.Чупрова.  Коэффициент Пирсона рассчитывается по формуле: КП =  х2  п+х2 где х2 - расчетное значение хи-квадрата, п - общее число наблюдений (объем выборки).  Коэффициент Чупрова позволяет учесть число групп по каждому признаку и определяется следующим образом:  х2  К Ч =  nV (k - 1)(*2 - 1) '  где k1 и k2 - соответственно число значений (групп) для первого и второго признаков или, по-другому, число строк и столбцов в таблице, а п - общее число наблюдений (объем выборки). 

Попробуем выполнить такие расчеты для нашего примера. х2  2,905  К П =  i  п +х2 V  = 0,234 ;  50 + 2,905 2,905 0,184  КЧ  х2  50 х^ (4 -1)(2 -1)  \  nj(k1 - 1)(k2 -1) \ Расчет обоих коэффициентов дает весьма малые величины, что свидетельствует об отсутствии связи между исследуемыми характеристиками. Это же подтверждают и оценки по таблице Чеддока: рассчитанные коэффициенты, по модулю меньшие 0,3, говорят об отсутствии корреляционной связи. Иначе говоря, использование и этих коэффициентовподтверждает ранее вы-сказанное соображение: анализируемая ситуация по своим параметрам соответствует опорным (ожидаемым) показателям и посему не требует введения каких-либо корректировок. 

31) Между признаками выборочной совокупности и признаками генеральной совокупности, как правило, существует некоторое расхождение, которое называется ошибкой статистического наблюдения. При массовом наблюдении ошибки неизбежны, но возникают они в результате действия различных причин. Величина возможной ошибки выборочного признака происходит из-за ошибок регистрации и ошибок репрезентативности. Ошибки регистрации, или технические ошибки, связаны с недостаточной квалификацией наблюдателей, неточностью подсчетов, несовершенством приборов и т. п.

Под ошибкой репрезентативности (представительства) понимают расхождение между выборочной характеристикой и предполагаемой характеристикой генеральной совокупности. Ошибки репрезентативности бывают случайными и систематическими. Систематические ошибки связаны с нарушением установленных правил отбора. Случайные ошибки объясняются недостаточно равномерным представлением в выборочной совокупности различных категорий единиц генеральной совокупности.

В результате первой причины выборка легко может оказаться смещенной, так как при отборе каждой единицы допускается ошибка, всегда направленная в одну и ту же сторону. Эта ошибка получила название ошибки смещения. Ее размер может превышать величину случайной ошибки. Особенность ошибки смещения состоит в том, что, являясь постоянной частью ошибки репрезентативности, она увеличивается с увеличением объема выборки. Случайная же ошибка с увеличением объема выборки уменьшается. Кроме того, величину случайной ошибки можно определить, тогда как размер ошибки смещения практически определить очень сложно, а иногда и невозможно, поэтому важно знать причины, вызывающие ошибку смещения, и предусмотреть мероприятия по ее устранению.

Ошибки смещения бывают преднамеренные и непреднамеренные. Причиной возникновения преднамеренной ошибки является тенденциозный подход к выбору единиц из генеральной совокупности. Чтобы не допустить появление такой ошибки, необходимо соблюдать принцип случайности отбора единиц.

Непреднамеренные ошибки могут возникать на стадии подготовки выборочного наблюдения, формирования выборочной совокупности и анализа ее данных. Чтобы не допустить появление таких ошибок, необходима хорошая основа выборки, т. е. та генеральная совокупность, из которой предполагается производить отбор, например список единиц отбора. Основа выборки должна быть достоверной, полной и соответствовать цели исследования, а единицы отбора и их характеристики должны соответствовать действительному их состоянию на момент подготовки выборочного наблюдения. Нередки случаи, когда в отношении некоторых единиц, попавших в выборку, трудно собрать сведения из-за их отсутствия на момент наблюдения, нежелания дать сведения и т. п. В таких случаях эти единицы приходится заменять другими. Необходимо следить, чтобы замена осуществлялась равноценными единицами.

Случайная ошибка выборки возникает в результате случайных различий между единицами, попавшими в выборку, и единицами генеральной совокупности, т. е. она связана со случайным отбором. Теоретическим обоснованием появления случайных ошибок выборки является теория вероятностей и ее предельные теоремы.

Сущность предельных теорем состоит в том, что в массовых явлениях совокупное влияние различных случайных причин на формирование закономерностей и обобщающих характеристик будет сколь угодно малой величиной или практически не зависит от случая. Так как случайная ошибка выборки возникает в результате случайных различий между единицами выборочной и генеральной совокупностей, то при достаточно большом объеме выборки она будет сколь угодно мала.

Предельные теоремы теории вероятностей позволяют определять размер случайных ошибок выборки. Различают среднюю (стандартную) и предельную ошибку выборки. Под средней (стандартной) ошибкой выборки понимают такое расхождение между средней выборочной и генеральной совокупностями (~ —), которое не превышает ±. Предельной ошибкой выборки принято считать максимально возможное расхождение (~ —), т. е. максимум ошибки при заданной вероятности ее появления.

В математической теории выборочного метода сравниваются средние характеристики признаков выборочной и генеральной совокупностей и доказывается, что с увеличением объема выборки вероятность появления больших ошибок и пределы максимально возможной ошибки уменьшаются. Чем больше обследуется единиц, тем меньше будет величина расхождений выборочных и генеральных характеристик. На основании теоремы, доказанной П.Л. Чебышевым, величину стандартной ошибки простой случайной выборки при достаточно большом объеме выборки (n) можно определить по формуле

– стандартная ошибка.

Из этой формулы средней (стандартной) ошибки простой случайной выборки видно, что величина зависит от изменчивости признака в генеральной совокупности (чем больше вариация признака, тем больше ошибка выборки) и от объема выборки n (чем больше обследуется единиц, тем меньше будет величина расхождений выборочных и генеральных характеристик).

Академик A.M. Ляпунов доказал, что вероятность появления случайной ошибки выборки при достаточно большом ее объеме подчиняется закону нормального распределения. Эта вероятность определяется по формуле

В математической статистике употребляют коэффициент доверия t, значения функции F(t) табулированы при разных его значениях, при этом получают соответствующие уровни доверительной вероятности (табл. 6.1).

Таблица 6.1

Коэффициент доверия t и соответствующие уровни доверительной вероятности

Коэффициент доверия позволяет вычислить предельную ошибку выборки,

т. е. предельная ошибка выборки равна t-кратному числу средних ошибок выборки.

Таким образом, величина предельной ошибки выборки может быть установлена с определенной вероятностью. Как видно из последней графы табл. 6.1, вероятность появления ошибки равной или большей утроенной средней ошибки выборки, т. е.

крайне мала и равна 0,003(1–0,997). Такие маловероятные события считаются практически невозможными, а потому величину

можно принять за предел возможной ошибки выборки.

Выборочное наблюдение дает возможность определить среднюю арифметическую выборочной совокупности и величину предельной ошибки этой средней, которая показывает (с определенной вероятностью), насколько выборочная величина может отличаться от генеральной средней в большую или меньшую сторону. Тогда величина генеральной средней будет представлена интервальной оценкой, для которой нижняя граница будет равна

Интервал, в который с данной степенью вероятности будет заключена неизвестная величина оцениваемого параметра, называют доверительным, а вероятность Р – доверительной вероятностью. Чаще всего доверительную вероятность принимают равной 0,95 или 0,99, тогда коэффициент доверия t равен соответственно 1,96 и 2,58. Это означает, что доверительный интервал с заданной вероятностью заключает в себе генеральную среднюю.

Наряду с абсолютной величиной предельной ошибки выборки рассчитывается и относительная ошибка выборки, которая определяется как процентное отношение предельной ошибки выборки к соответствующей характеристике выборочной совокупности:

Чем больше величина предельной ошибки выборки, тем больше величина доверительного интервала и тем, следовательно, ниже точность оценки. Средняя (стандартная) ошибка выборки зависит от объема выборки и степени вариации признака в генеральной совокупности.

31-32) Статистическое наблюдение можно организовать как сплошное и несплошное. Сплошноепредусматривает обследование всех единиц изучаемой совокупности явления, несплошное – лишь ее части. К несплошному относится и выборочное наблюдение.

Выборочное наблюдение является одним из наиболее широко применяемых видов несплошного наблюдения. В основе этого наблюдения лежит идея о том, что отобранная в случайном порядке некоторая часть единиц может представлять всю изучаемую совокупность явления по интересующим исследователя признакам. Целью выборочного наблюдения является получение информации прежде всего для определения сводных обобщающих характеристик всей изучаемой совокупности. По своей цели выборочное наблюдение совпадает с одной из задач сплошного наблюдения, и поэтому встает вопрос о том, какое из двух видов наблюдения – сплошное или выборочное – целесообразнее провести.

При решении этого вопроса необходимо исходить из следующих основных требований, предъявляемых к статистическому наблюдению:

• информация должна быть достоверной, т. е. максимально соответствовать реальной действительности;

• сведения должны быть достаточно полными для решения задач исследования;

• отбор информации должен быть проведен в максимально сжатые сроки для использования ее в оперативных целях;

• денежные и трудовые затраты на организацию и проведение должны быть минимальными.

При выборочном наблюдении эти требования обеспечиваются в большей мере, чем при сплошном. Преимущества этого метода по сравнению со сплошным можно оценить, если оно организовано и проведено в строгом соответствии с научными принципами теории выборочного метода, а именно обеспечение случайности отбора единиц и достаточного их числа. Соблюдение этих принципов позволяет получить такую совокупность единиц, которая представляет всю изучаемую совокупность по интересующим исследователя признакам, т. е. является репрезентативной (представительной).

При проведении выборочного наблюдения обследуются не все единицы изучаемого объекта, т. е. не все единицы совокупности, а лишь некоторая специально отобранная часть. Первый принцип отбора– обеспечение случайности – заключается в том, что при отборе каждой из единиц изучаемой совокупности обеспечивается равная возможность попасть в выборку. Случайный отбор – это не беспорядочный отбор, а отбор при соблюдении определенной методики, например осуществление отбора по жребию, применение таблицы случайных чисел и т. д.

Второй принцип отбора – обеспечение достаточного числа отобранных единиц – тесно связан с понятием репрезентативности выборки. Так как любое выборочное наблюдение проводится с определенной целью и четко сформулированными конкретными задачами, то понятие репрезентативности как раз и связано с целью и задачами исследования. Отобранная из всей изучаемой совокупности часть должна быть репрезентативной прежде всего в отношении тех признаков, которые изучаются или оказывают существенное влияние на формирование сводных обобщающих характеристик.

В выборочном наблюдении используются понятия «генералъная совокупность» – изучаемая совокупность единиц, подлежащая изучению по интересующим исследователя признакам, и«выборочная совокупность» – случайно отобранная из генеральной совокупности некоторая ее часть. К данной выборке предъявляется требование репрезентативности, т. е. при изучении лишь части генеральной совокупности полученные выводы можно применять ко всей совокупности. Характеристиками генеральной и выборочной совокупностей могут служить средние значения изучаемых признаков, их дисперсии и средние квадратические отклонения, мода и медиана и др.

Исследователя могут интересовать и распределения единиц по изучаемым признакам в генеральной и выборочной совокупностях. В этом случае частоты называются соответственно генеральными и выборочными.

Система правил отбора и способов характеристики единиц изучаемой совокупности составляет содержание выборочного метода, суть которого состоит в получении первичных данных при наблюдении выборки с последующим обобщением, анализом и их распространением на всю генеральную совокупность с целью получения достоверной информации об исследуемом явлении.

Репрезентативность выборки обеспечивается соблюдением принципа случайности отбора объектов совокупности в выборку. Если совокупность является качественно однородной, то принцип случайности реализуется простым случайным отбором объектов выборки. Простым случайным отбором называют такую процедуру образования выборки, которая обеспечивает для каждой единицы совокупности одинаковую вероятность быть выбранной для наблюдения, для любой выборки заданного объема.

Таким образом, цель выборочного метода – сделать вывод о значении признаков генеральной совокупности на основе информации случайной выборки из этой совокупности.

Ошибки выборочного наблюдения

Между признаками выборочной совокупности и признаками генеральной совокупности, как правило, существует некоторое расхождение, которое называется ошибкой статистического наблюдения. При массовом наблюдении ошибки неизбежны, но возникают они в результате действия различных причин. Величина возможной ошибки выборочного признака происходит из-за ошибок регистрации и ошибок репрезентативности. Ошибки регистрации, или технические ошибки, связаны с недостаточной квалификацией наблюдателей, неточностью подсчетов, несовершенством приборов и т. п.

Под ошибкой репрезентативности (представительства) понимают расхождение между выборочной характеристикой и предполагаемой характеристикой генеральной совокупности. Ошибки репрезентативности бывают случайными и систематическими. Систематическиеошибки связаны с нарушением установленных правил отбора. Случайные ошибки объясняются недостаточно равномерным представлением в выборочной совокупности различных категорий единиц генеральной совокупности.

В результате первой причины выборка легко может оказаться смещенной, так как при отборе каждой единицы допускается ошибка, всегда направленная в одну и ту же сторону. Эта ошибка получила название ошибки смещения. Ее размер может превышать величину случайной ошибки. Особенность ошибки смещения состоит в том, что, являясь постоянной частью ошибки репрезентативности, она увеличивается с увеличением объема выборки. Случайная же ошибка с увеличением объема выборки уменьшается. Кроме того, величину случайной ошибки можно определить, тогда как размер ошибки смещения практически определить очень сложно, а иногда и невозможно, поэтому важно знать причины, вызывающие ошибку смещения, и предусмотреть мероприятия по ее устранению.

Ошибки смещения бывают преднамеренные и непреднамеренные. Причиной возникновенияпреднамеренной ошибки является тенденциозный подход к выбору единиц из генеральной совокупности. Чтобы не допустить появление такой ошибки, необходимо соблюдать принцип случайности отбора единиц.

Непреднамеренные ошибки могут возникать на стадии подготовки выборочного наблюдения, формирования выборочной совокупности и анализа ее данных. Чтобы не допустить появление таких ошибок, необходима хорошая основа выборки, т. е. та генеральная совокупность, из которой предполагается производить отбор, например список единиц отбора. Основа выборки должна быть достоверной, полной и соответствовать цели исследования, а единицы отбора и их характеристики должны соответствовать действительному их состоянию на момент подготовки выборочного наблюдения. Нередки случаи, когда в отношении некоторых единиц, попавших в выборку, трудно собрать сведения из-за их отсутствия на момент наблюдения, нежелания дать сведения и т. п. В таких случаях эти единицы приходится заменять другими. Необходимо следить, чтобы замена осуществлялась равноценными единицами.

Случайная ошибка выборки возникает в результате случайных различий между единицами, попавшими в выборку, и единицами генеральной совокупности, т. е. она связана со случайным отбором. Теоретическим обоснованием появления случайных ошибок выборки является теория вероятностей и ее предельные теоремы.

Сущность предельных теорем состоит в том, что в массовых явлениях совокупное влияние различных случайных причин на формирование закономерностей и обобщающих характеристик будет сколь угодно малой величиной или практически не зависит от случая. Так как случайная ошибка выборки возникает в результате случайных различий между единицами выборочной и генеральной совокупностей, то при достаточно большом объеме выборки она будет сколь угодно мала.

Предельные теоремы теории вероятностей позволяют определять размер случайных ошибок выборки. Различают среднюю (стандартную) и предельную ошибку выборки. Под средней (стандартной) ошибкой выборки понимают такое расхождение между средней выборочной и генеральной совокупностями (~ —), которое не превышает ±. Предельной ошибкой выборки принято считать максимально возможное расхождение (~ —), т. е. максимум ошибки при заданной вероятности ее появления.

В математической теории выборочного метода сравниваются средние характеристики признаков выборочной и генеральной совокупностей и доказывается, что с увеличением объема выборки вероятность появления больших ошибок и пределы максимально возможной ошибки уменьшаются. Чем больше обследуется единиц, тем меньше будет величина расхождений выборочных и генеральных характеристик. На основании теоремы, доказанной П.Л. Чебышевым, величину стандартной ошибки простой случайной выборки при достаточно большом объеме выборки (n) можно определить по формуле

– стандартная ошибка.

Из этой формулы средней (стандартной) ошибки простой случайной выборки видно, что величина зависит от изменчивости признака в генеральной совокупности (чем больше вариация признака, тем больше ошибка выборки) и от объема выборки n (чем больше обследуется единиц, тем меньше будет величина расхождений выборочных и генеральных характеристик).

Академик A.M. Ляпунов доказал, что вероятность появления случайной ошибки выборки при достаточно большом ее объеме подчиняется закону нормального распределения. Эта вероятность определяется по формуле

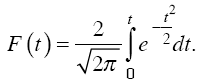
В математической статистике употребляют коэффициент доверия t, значения функции F(t)табулированы при разных его значениях, при этом получают соответствующие уровни доверительной вероятности (табл. 6.1).

Таблица 6.1