
- •Глава 4. Повторные независимые испытания
- •§ 4.1. Формула Бернулли
- •§ 4.2. Локальная теорема Муавра – Лапласа
- •§ 4.3. Интегральная теорема Муавра – Лапласа
- •§ 4.4. Теоремы Пуассона3
- •Раздел 2 случайные величины
- •Глава 5. Дискретная случайная величина
- •§ 5.1. Функция распределения дискретной случайной величины
- •§ 5.2. Основные числовые характеристики дискретной случайной величины
- •§ 5.3. Основные законы распределения случайных величин
- •§ 5.3.1. Биномиальный закон распределения
- •§ 5.3.2. Закон распределения Пуассона
- •Глава 6. Непрерывная случайная величина
- •§ 6.1. Функция распределения непрерывной случайной величины
- •§ 6.2. Функция плотности вероятности непрерывной случайной величины
- •§ 6.3. Основные числовые характеристики непрерывной случайной величины
- •§ 6.4. Основные законы распределения непрерывных случайных величин
- •§ 6.4.1. Равномерный закон распределения
- •Глава 7. Нормальный закон распределения
- •§ 7.1. Свойства функции плотности вероятности (кривой Гаусса) нормального закона распределения
- •§ 7.2. Математическое ожидание и дисперсия нормальной случайной величины
- •§ 7.3. Функция распределения случайной величины, распределенной по нормальному закону
- •§ 7.4. Свойства случайной величины, имеющей нормальный закон распределения
- •Глава 8. Предельные теоремы теории вероятности
- •§ 8.1. Закон больших чисел. Основные теоремы
- •1. Лемма Маркова
- •2. Неравенство Чебышева
- •§ 8.2. Центральная предельная теорема
§ 4.4. Теоремы Пуассона3
При
большом числе испытаний
,
постоянной малой вероятности
наступления события А
в
каждом испытании
![]() ,
и при выполнении
условия
,
и при выполнении
условия
![]() ,
вероятность
того, что в n
независимых
испытаниях
событие А
наступит
ровно m
раз,
определяется соответствии с
теоремой Пуассона:
,
вероятность
того, что в n
независимых
испытаниях
событие А
наступит
ровно m
раз,
определяется соответствии с
теоремой Пуассона:
![]() (1.31)
(1.31)
где n — число испытаний Бернулли;
m — число испытаний, в которых наступило событие А;
![]() — параметр
Пуассоновского распределения, называемый
еще
средней
интенсивностью.
— параметр
Пуассоновского распределения, называемый
еще
средней
интенсивностью.
Теорему
можно доказать путем замены в формуле
Бернулли вероятности
р
на
![]() вычисления
ее предела при
/
вычисления
ее предела при
/
Значения
функции Пуассона
также
могут быть определены по табл.
8 Приложения для заданных значений m
и
![]() .
.
С лучайные события, к которым может быть применена теорема Пуассона, называют еще редкими событиями ввиду малой вероятности наступления события А в каждом испытании.
Пример 4.4. Вероятность изготовления бракованной отливки равна 0,002. Определить вероятность того, что из выпущенных 500 отливок количество бракованных составит:
а) 2;
б) более двух.
Решение.
Проводится 500 независимых испытаний, состоящих в проверке брака отливки. Для каждой из 500 отливок вероятность события А – отливка бракованная - по условию постоянна и равна:
![]()
В задаче
число испытаний велико n=500,
р=0,002 – мала, параметр Пуассона
![]()
А.
Требуется определить вероятность того,
что из 500 отливок ровно 2 будут бракованными,
т. е. вероятность
![]()
Так как
испытания удовлетворяют условиям схемы
Бернулли, n>>100,
р – мала,
![]() то эту вероятность можно определить по
формуле Пуассона (1.31):
то эту вероятность можно определить по
формуле Пуассона (1.31):
![]()
(вероятность
можно определить и по табл. 8 Приложений
значений функции Пуассона для
![]() и m=2).
и m=2).
Б.
Требуется определить вероятность того,
что из 500 отливок более 2 будут бракованные,
т. е. вероятность
![]()
При этом по теореме сложения для несовместных событий (1.13):
![]()
так как
события
![]() несовместны. В данном случае целесообразно
перейти к противоположному событию
(что будет не больше 2 бракованных
отливок,
несовместны. В данном случае целесообразно
перейти к противоположному событию
(что будет не больше 2 бракованных
отливок,
![]() ),
и воспользоваться следствием (1.15):
),
и воспользоваться следствием (1.15):
![]()
Так как
испытания удовлетворяют условиям схемы
Бернулли, n>>100,
р – мала,
![]() ,
то вероятности можно определить по
формуле Пуассона (1.31):
,
то вероятности можно определить по
формуле Пуассона (1.31):
![]()

Раздел 2 случайные величины
Дискретная случайная величина
Непрерывная случайная величина
Нормальный закон распределения
Предельные теоремы теории вероятностей
Одним из основных понятий теории вероятностей является, наряду со случайным событием, понятие случайной величины.
• Случайная величина — это переменная, которая в результате испытания принимает одно из своих возможных значений, причем заранее не известно, какое именно, так как оно зависит от случая.
Связь
случайной величины и случайного события
заключается в том, что принятие случайной
величиной некоторого числового значения
из набора возможных (т. е. выполнение
равенства
![]() )4
есть случайное событие, характеризующееся
вероятностью
)4
есть случайное событие, характеризующееся
вероятностью
![]() .
.
Примеры случайных величин:
число очков, выпавших на верхней грани игрального кубика;
число студентов, пришедших на лекцию;
расстояние от центра мишени до точки попадания при выстреле;
сумма выплаты по очередному страховому случаю и т. п.
Для определения случайной величины необходимо задать ее закон распределения.
• Закон распределения — соотношение, устанавливающее связь между возможными значениями случайной величины и соответствующими вероятностями, с которыми случайная величина принимает эти значения.
Для практического применения не всегда необходимо иметь полное представление о случайной величине, достаточно знать некоторые ее числовые характеристики, дающие суммарное представление о случайной величине, к которым, прежде всего, относятся математическое ожидание и дисперсия.
• Математическое ожидание М(Х) — это число, характеризующее среднее значение случайной величины X.
Свойства математического ожидания:
математическое ожидание постоянной величины С=const равно этой величине:
М(С)=С;
математическое ожидание произведения постоянной величины С=const и случайной величины X равно произведению этой константы на математическое ожидание случайной величины (константу можно вынести за знак математического ожидания):
М(С*Х)=С*М(Х);
математическое ожидание алгебраической суммы п случайных величин
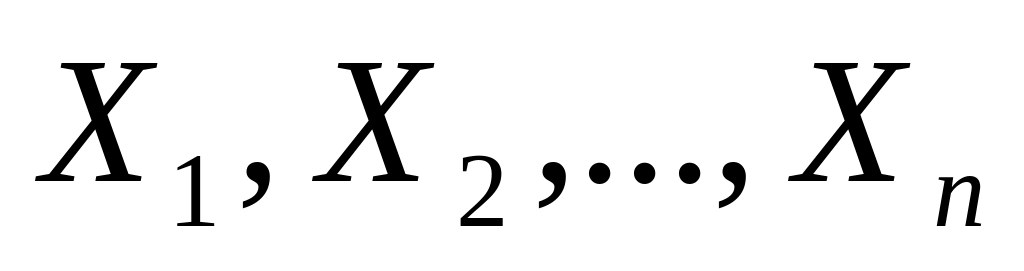 равно алгебраической сумме математических
ожиданий этих случайных величин:
равно алгебраической сумме математических
ожиданий этих случайных величин:
![]()
математическое ожидание произведения n независимых случайных величин равно произведению математических ожиданий этих случайных величин:
![]()
математическое ожидание алгебраической суммы случайной величины X и постоянной величины С=const равно алгебраической сумме этой константы и математического ожидания случайной величины:
![]()
в
частности,
![]()
математическое ожидание среднего арифметического значения n одинаково распределенных (имеющих одинаковые законы распределения) взаимно независимых случайных величин равно математическому ожиданию этих величин:
![]()
Дисперсия характеризует разброс или рассеяние значений случайной величины около ее математического ожидания.
Дисперсия — это математическое ожидание квадрата отклонения случайной величины от ее математического ожидания:
![]()
Свойства дисперсии:
дисперсия постоянной величины C=const равна нулю:
![]()
дисперсия произведения постоянной величины С=const и случайной величины X равна произведению квадрата этой константы на дисперсию случайной величины (константу можно вынести за знак дисперсии, возведя ее в квадрат):
![]()
дисперсия алгебраической суммы или разности n независимых случайных величин равна сумме дисперсий этих случайных величин:
![]()
дисперсия алгебраической суммы случайной величины Х и постоянной величины С=const равна дисперсии случайной величины:
![]()
в
частности,
![]()
дисперсии суммы и среднего арифметического значения n одинаково распределенных (имеющих одинаковые законы распределения) взаимно независимых случайных величин , дисперсия каждой из которых равна
 ,
равны
,
равны
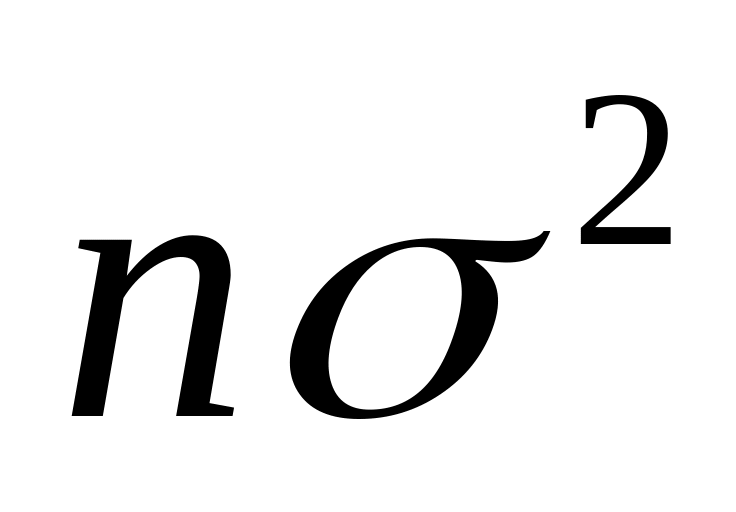 и соответственно:
и соответственно:
![]()
![]()
Формула упрощенного вычисления дисперсии имеет вид:
![]() (1.32)
(1.32)
Действительно,
![]()
В зависимости от характера области возможных значений выделяют два типа случайных величин: дискретные и непрерывные.
