Глава 8. Предельные теоремы теории вероятности

Данная тема важна для понимания методов математической статистики. Она включает в себя ряд теорем, устанавливающих при определенных условиях устойчивость частости и средней арифметической (теоремы Бернулли, Пуассона, Чебышева, Маркова) или устойчивость закона распределения (теорема Ляпунова).

В широком смысле под законом больших чисел понимается свойство устойчивости массовых явлений, состоящее в том, что средний резудь. тат действия большого числа случайных явлений практически перестает быть случайным и может быть предсказан с достаточной определенностью.

В узком смысле под законом больших чисел понимают совокупность теорем, устанавливающих факт приближения средних характеристик, полученных по результатам большого числа наблюдений, к некоторым постоянным величинам.

Пусть дана последовательность случайных величин а случайные величины представляют собой заданные симметрические функции от первых п членов последовательности Тогда если существует последовательность чисел такая, что для любого выполняется , то говорят, что последовательность подчиняется закону больших чисел.

§ 8.1. Закон больших чисел. Основные теоремы

1. Лемма Маркова

Если случайная величина X не принимает отрицательных значений, то для любого положительного числа т выполняется:

. (1.50)

Д оказательство.

Для определенности предположим, что X — непрерывная случайная величина с плотностью распределения вероятностей f(х). По определению математического ожидания: . Выражение перепишем в виде , откуда, учитывая, что оба слагаемых в правой части положительны, следует .

Так как , то .

В итоге, учитывая, что М(Х)>0, получим .

2. Неравенство Чебышева

Для любой случайной величины X, имеющей конечную дисперсию, при каждом имеет место неравенство:

. (1.51)

Д оказательство.

Рассмотрим дискретную случайную величину X, закон распределения которой описывается рядом распределения Тогда ряд распределения случайной величины имеет вид:

Без ограничения общности можно считать, что первые k значений этой случайной величины меньше заданного , а остальные значения не меньше заданного . Тогда на основании теоремы сложения вероятностей получим:

.

Далее запишем формулу дисперсии D(X) в виде:

,

откуда , что приводит к .

3. Теорема Чебышева (частный случай)

Если — последовательность наблюдений случайной величины X, имеющей конечную дисперсию, то каково бы ни было

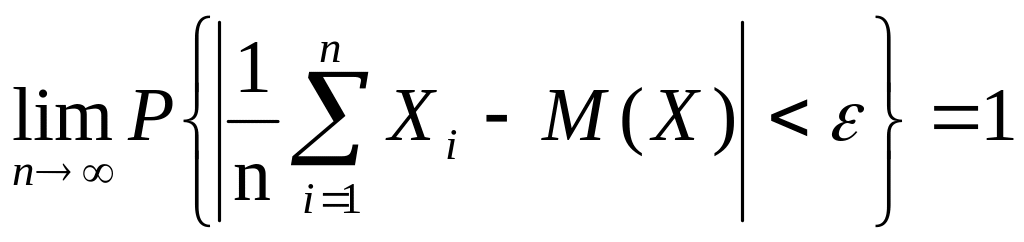. (1.52)

4. Теорема Чебышева (общий случай)

Если — последовательность попарно независимых случайных величин, имеющих конечные дисперсии, ограниченные одной и той же постоянной С, т. е. то каково бы ни было

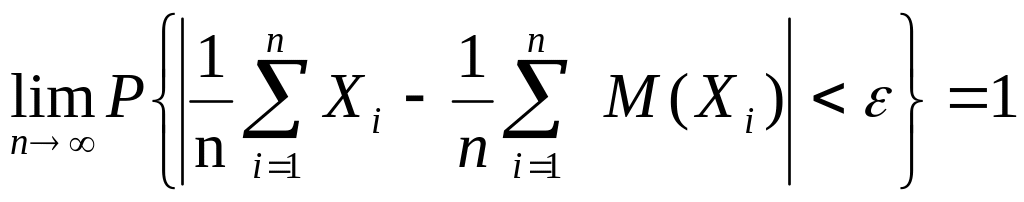. (1.53)

Д оказательство.

Рассмотрим случайную величину .

В соответствии со свойствами математического ожидания и дисперсии:

, .

По условию теоремы , поэтому .

В соответствии с неравенством Чебышева:

.

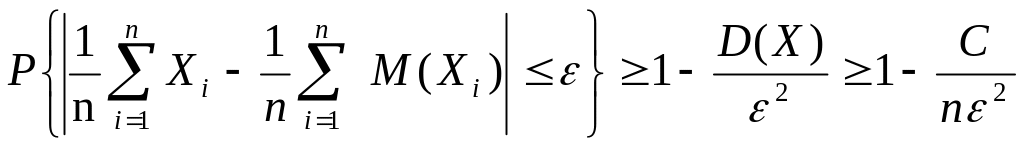5. Теорема Бернулли

Пусть m — число наступления события А в серии n независимых испытаний, а р — есть вероятность наступления события в каждом из ис пытаний. Тогда каково бы ни было

. (1.54)

6. Теорема Пуассона

Пусть m — число наступления события А в серии n независимых ис пытаний, а — есть вероятность наступления события в i-м испытании Тогда каково бы ни было

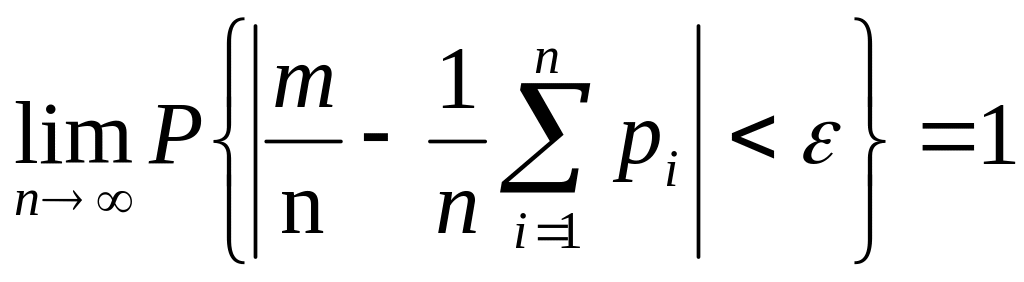. (1.55)