
- •Глава 4. Повторные независимые испытания
- •§ 4.1. Формула Бернулли
- •§ 4.2. Локальная теорема Муавра – Лапласа
- •§ 4.3. Интегральная теорема Муавра – Лапласа
- •§ 4.4. Теоремы Пуассона3
- •Раздел 2 случайные величины
- •Глава 5. Дискретная случайная величина
- •§ 5.1. Функция распределения дискретной случайной величины
- •§ 5.2. Основные числовые характеристики дискретной случайной величины
- •§ 5.3. Основные законы распределения случайных величин
- •§ 5.3.1. Биномиальный закон распределения
- •§ 5.3.2. Закон распределения Пуассона
- •Глава 6. Непрерывная случайная величина
- •§ 6.1. Функция распределения непрерывной случайной величины
- •§ 6.2. Функция плотности вероятности непрерывной случайной величины
- •§ 6.3. Основные числовые характеристики непрерывной случайной величины
- •§ 6.4. Основные законы распределения непрерывных случайных величин
- •§ 6.4.1. Равномерный закон распределения
- •Глава 7. Нормальный закон распределения
- •§ 7.1. Свойства функции плотности вероятности (кривой Гаусса) нормального закона распределения
- •§ 7.2. Математическое ожидание и дисперсия нормальной случайной величины
- •§ 7.3. Функция распределения случайной величины, распределенной по нормальному закону
- •§ 7.4. Свойства случайной величины, имеющей нормальный закон распределения
- •Глава 8. Предельные теоремы теории вероятности
- •§ 8.1. Закон больших чисел. Основные теоремы
- •1. Лемма Маркова
- •2. Неравенство Чебышева
- •§ 8.2. Центральная предельная теорема
Глава 4. Повторные независимые испытания
При
решении вероятностных задач часто
приходится сталкиваться с ситуациями,
в которых одно и то же испытание
повторяется многократно. Под испытанием
понимается осуществление определенного
комплекса условий, в результате которых
может произойти (или нет) то или иное
событие пространства
![]() элементарных событий.
элементарных событий.
Повторные независимые испытания — многократные испытания, в которых вероятность появления события А в каждом испытании не меняется в зависимости от исходов других испытаний. Впервые схема независимых испытаний была рассмотрена Я. Бернулли1 для важнейшего частного случая k=2.
Под схемой Бернулли понимают проведение серии в n испытаний, в каждом из которых возможны два исхода: либо наступит событие А, либо не наступит, т. е. произойдет противоположное ему и при этом:
все п испытаний независимы;
вероятность события А в каждом отдельном испытании постоянна и не меняется от испытания к испытанию:
![]()

П ример. К случайным событиям, удовлетворяющим условиям схемы Бернулли, относятся: многократное подбрасывание монеты (событие А – например, выпадение «орла»), многократная стрельба по мишени (событие А – например, попадание в мишень) и т. п.
§ 4.1. Формула Бернулли
В
случае небольшого числа испытаний n
вероятность
![]() того,
что в n
независимых
испытаниях событие А
наступит
ровно m
раз,
определяется
в соответствии с формулой
Бернулли:
того,
что в n
независимых
испытаниях событие А
наступит
ровно m
раз,
определяется
в соответствии с формулой
Бернулли:
![]() (1.24)
(1.24)
где n – число испытаний Бернулли;
m – число испытаний, в которых наступило событие А;
q=1-p
– вероятность противоположного события
![]() ;
;
![]() – число сочетаний
из n
элементов по m
(1.6).
– число сочетаний
из n
элементов по m
(1.6).
Д оказательство.
оказательство.
Обозначим
через
![]() появление
события А
в
i-м
испытании. Вероятность
того, что А,
наступают
при определенных m
испытаниях
(например, с
номерами
появление
события А
в
i-м
испытании. Вероятность
того, что А,
наступают
при определенных m
испытаниях
(например, с
номерами
![]() ),
а при остальных n-m
не
наступает, равна:
),
а при остальных n-m
не
наступает, равна:
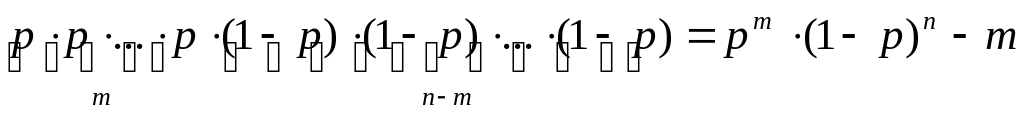 .
.
По
теореме сложения вероятностей для
несовместных событий (1.13), искомая
вероятность
![]() равна
сумме вероятностей полученного значения
для
всех возможных способов m
появлений
события А
в
n
испытаниях. В соответствии
с правилами комбинаторики, число таких
способов определяется
числом сочетаний из n
по
m
(1.6):
равна
сумме вероятностей полученного значения
для
всех возможных способов m
появлений
события А
в
n
испытаниях. В соответствии
с правилами комбинаторики, число таких
способов определяется
числом сочетаний из n
по
m
(1.6):
![]()
 .
.
Пример 4.1. После года хранения на складе в среднем 10% аккумуляторов выходит из строя. Определить вероятность того, что после года хранения из 12 аккумуляторов окажутся годными:
а) 10,
б) больше половины.
Решение.
Проводится
12 независимых испытаний, состоящих в
проверке годности аккумулятора. Для
каждого из 12 аккумуляторов вероятность
события А – аккумулятор после года
хранения годный – по условию постоянна
и равна:
![]()
А.
Требуется определить вероятность того,
что из 12 аккумуляторов ровно 10 будут
годными, т. е. вероятность
![]() .
Поскольку испытания удовлетворяют
условиям схемы Бернулли, то эту вероятность
можно определить по формуле Бернулли
(1.24):
.
Поскольку испытания удовлетворяют
условиям схемы Бернулли, то эту вероятность
можно определить по формуле Бернулли
(1.24):
![]()
Б.
Требуется определить вероятность того,
что из 12 аккумуляторов более 12/2=6 будут
годными, т. е. вероятность
![]() .
При этом по теореме сложения для
несовместных событий (1.13):
.
При этом по теореме сложения для
несовместных событий (1.13):
![]() ,
,
так как
события
![]() не
совместны.
не
совместны.
Так как испытания удовлетворяют условиям схемы Бернулли, то вероятности можно определить по формуле Бернулли (1.24):
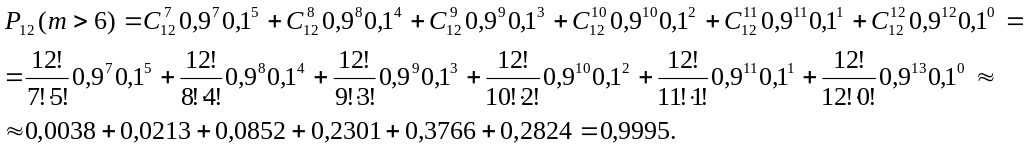

При вычислении вероятностей в условиях большого числа испытаний n можно столкнуться со значительными вычислительными трудностями. В связи с этим возникла необходимость в построении асимптотических (приближенных) формул, позволяющих с достаточной степенью точности определить . Одними из них являются теоремы Муавра – Лапласа2
