Еквіпотенціальні поверхні

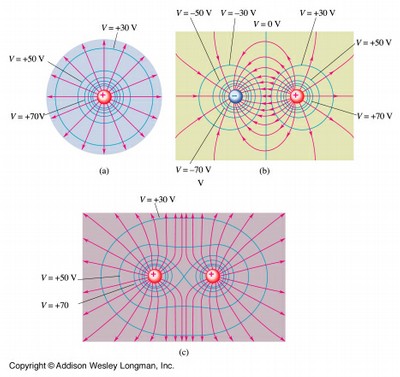
ЩО ТАКЕ ЕКВІПОТЕНЦІАЛЬНА ПОВЕРХНЯ І ЯКА ЇЇ КОНФІГУРАЦІЯ ДЛЯ ТОЧКОВИХ ЗАРЯДІВ?

Еквіпотенціа́льна пове́рхня (лінія рівного потенціалу) — поверхня, в усіх точках якої однаковий потенціал.

Еквіпотенціальні поверхні перпендикулярні до силових ліній поля.

ЕЛЕКИРИЧНЕ ПОЛЕ ТОЧКОВОГО ЗАРЯДУ.

Навколо електричних зарядів існує електричне поле. Силова характеристика, що чисельно дорівнює відношенню сили, яка діє на заряд, поміщений у дану точку простору, до значення цього заряду, називається напруженістю електричного поля.

Сила F_q, що діє на заряд q, поміщений в електричне поле з напруженістю  :

Напрям напруженості електричного поля збігається з напрямом сили,

що діє на позитивний заряд у даній точці (q>0). Напрям векторів  і   протилежні якщо q<0.

За принципом суперпозиції полів результуюча напруженість електричного поля кількох зарядів дорівнює геометричній сумі напруженостей полів кожного окремого заряду.

 .

Напруженість електричного поля точкового заряду:

Напруженість рівномірно зарядженої нескінченної площини:

- поверхнева густина заряду.

Напруженість електричного поля сфери радіуса R, заряд якої рівномірно розподілений по її поверхні:

Е=0, при r < R  при r і R 

ПРИНЦИП СУПЕР ПОЗИЦІЇ ПОЛІВ.

Принцип суперпозиції – один із найзагальніших законів у багатьох розділах фізики. Найпростіше формулювання принципу суперпозиції звучить так: результат впливу на частинку кількох зовнішніх сил є просто сума резульаттів впливу кожної із сил.

Найбільш відомий принцип суперпозиції в електростатиці, в якій він стверджує, що електростатичний потенціал, який створюється в даній точці системою зарядів, є сума потенціалів окремих зарядів.

Підкреслимо, що електродинамічний принцип суперпозиції не є непорушним законом природи, а є усього лише наслідком лінійності рівнянь Максвелла, тобто рівнянь класичної електродинаміки. Тому, коли ми виходимо за межі застосовності класичної електродинаміки, цілком варто очікувати порушення принципу суперпозиції.

Якщо E→1(r→) — поле системи зарядів №1, а E→2(r→) — поле системи зарядів №2, то при наявності зарядів обох систем:

E→(r→) = E→1(r→) + E→2(r→).

(4.1)

Рис. 8 пояснює сказане.

Рис.8: Принцип суперпозиції. Під час відсутності заряду q2 на спробний заряд q3 діє сила F→13 = q3E→1, а під час відсутності заряду q1 — сила F→23 = q3E→2. При наявності обох зарядів діюча сила дорівнює їхній сумі, F→3 = F→13 + F→23 = q3E→. Звідси випливає, що в місці перебування спробного заряду E→ = E→1 + E→2.

Найпростіша система складається з одного заряду. Отже, електричне поле системи зарядів дорівнює сумі полів, створюваних кожним зарядом окремо, під час відсутності інших зарядів:

E→(r→) = ∑ j qj ∣r→ −r→j∣2 r→ −r→j ∣r→ −r→j∣ .

(4.2)

Тут qj,r→j — заряд і радіус-вектор j-го заряду. Правило додавання (4.1)називають принципом суперпозиції, а формула (4.2)є наслідком принципу суперпозиції і закону Кулона.

Досліди показують, якщо на електричний заряд q діють одночасно електричні поля декількох зарядів, то результуюча сила дорівнює геометричній сумі сил, що діють з боку кожного поля окремо. Ця властивість електричних полів означає, що ці поля підлягають принципу суперпозиції: якщо в заданій точці простору різні заряджені частинки створюють електричні поля напруженістю  ,  ,  і т.д., то результуюча напруженість поля в цій точці дорівнює геометричній сумі напруженостей полів частинок, тобто: принцип суперпозиції (накладання) полів означає, що електричні поля під час накладання не впливають одне на одне.

Принцип суперпозиції дозволяє обчислити напруженість поля довільної системи зарядів, а не тільки точкових, зокрема і рівномірно зарядженої площини.

За рівномірного розподілу електричного заряду q по поверхні площею S поверхнева густина заряду s є сталою і дорівнює:

.

У фізиці доведено, що напруженість електричного поля нескінченої площини з поверхневою густиною заряду s однакова в довільній точці простору і дорівнює:

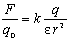, (4.1.8)

де e0 - електрична стала.

Формулу застосовують для розрахунку напруженості електричного поля біля заряджених тіл у тому разі, коли форма рівномірно зарядженої поверхні близька до площини і відстань від точки, в якій визначається напруженість поля, до поверхні тіла значно менша від розмірів тіла і відстані до краю зарядженої поверхні.

З рис. 7 видно, що напруженості полів, створених обома площинами, напрямлені в один бік. Отже, геометрична сума (згідно з принципом суперпозиції полів) є їх арифметичною сумою:

Поза площинами пластин їх напруженості напрямлені протилежно. Тому результуюча напруженість поля поза площинами дорівнює нулю і електричного поля в цих частинах простору немає.

Принцип суперпозиції є експериментальним фактом. В електродинаміку він розглядається як абсолютно точний у тім змісті, що ніякі відхилення від нього не виявлені. Принцип суперпозиції для електричного поля не настільки очевидний, як могло б показатися на перший погляд.

Наприклад, можна припустити, що він порушується в дуже сильному полі аналогічно тому, як у твердому тілі пружні напруження можна складати тільки за умови, що вони досить малі (при великих деформаціях тіло руйнується).

Однак експерименти свідчать, що навіть на поверхні важких ядер, де електричне поле досягає величезних значень, принцип суперпозиції виконується. Інша справа, що при полях, приблизно в 100 разів менших, виявляються ефекти поляризації вакууму в результаті народження електрон-позитронних пар. Це приводить до квантово-механічної нелінійності взаємодії зарядів.

РОБОТА ЕЛЕКТРИЧНОГО ПОЛЯ ПРИ ПЕРЕМІЩЕННІ ЗАРЯДУ.

На будь-який заряд q, внесений в електричне поле з напруженістю Е, діє сила F=Eq. При відсутності протидіючих сил (тертя, пружна деформація зв'язків тощо) заряд q під дією електричної сили рухатиметься з прискоренням:

              

і, отже, змінюватиме свою швидкість, а тому і кінетичну енергію. Це означає, що при переміщенні заряду в електричному полі виконується робота.Для обчислення цієї роботи розглянемо переміщення пробного заряду q_oвздовж лінії напруженості електричного поля точкового заряду q між точками 1 і 2 (мал.1). На заряд q_o в точці 1, що знаходиться на відстані r від точкового заряду q_, діє сила

               , де  .

Поділимо відстань між точками 1 і 2 на такі малі відрізки dr, щоб напруженість Е, а отже силу F=Eq_о у всіх точках такого відрізка можна було б вважати сталими. Тоді елементарна робота dA на шляху dr обчислюватиметься за формулою (напрям переміщення і дії сили збігаються)

                              .

Робота на деякому кінцевому відрізку між точками 1 і 2 визначатиметься інтегральною сумою

                                    .

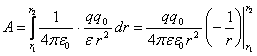Отже,

                             .

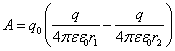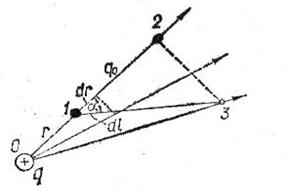
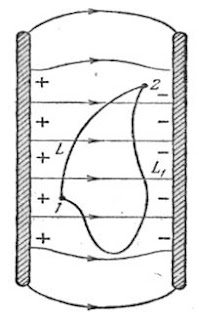
Тепер розглянемо випадок, коли точки 1і 3 розміщені не на одній силовій лінії, тобто коли напрями переміщення і дії сили не збігаються, а утворюють кут α. Візьмемо точки 2 і 3 на однаковій відстані від заряду q. Елементарна робота на шляху dl дорівнює

                        

Оскільки  , то  . Інтегрування цього виразу приводить до попереднього результату.

Отже, робота по переміщенню заряду q_o між точками 1 і 2 та точками 1 і 3 однакова. З цього випливає, що робота на шляху 0-3 дорівнює роботі на шляху 0-1-3. Це означає, що робота по переміщенню зарядуq_o в електростатичному полі не залежить від форми шляху і визначається тільки відносним розміщенням початкової і кінцевої точок цього шляху.

Як відомо, силове поле, в якому робота не залежить від форми шляху, є потенціальним полем. Отже, електростатичне поле – це поле потенціальне.

В потенціальному полі робота на довільному замкненому шляху, коли початкова і кінцева точки переміщення збігаються, дорівнює нулю. Справді, в цьому разі точки 1 і 2 збігатимуться, їх відстані r₁ і r₂ від заряду q будуть рівними. При цьому доданки в дужках у формулі

              

матимуть однакові значення, а їх різниця дорівнюватиме нулю.

 

Аналітично цей висновок можна записати так:

               ,

де інтегральна сума обчислюється вздовж замкненого шляху L.

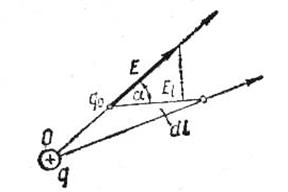
Добуток   визначає проекцію вектора напруженості Е на напрям переміщення dl заряду q_o (мал.2). Оскільки  , то після скорочення дістанемо

               , або  .

Цей інтеграл назиають циркуляцією вектора напруженості Е по замкненому контуру. Отже, циркуляція вектора напруженості електростатичного поля (як і будь-якого іншого потенціального поля) дорівнює нулю.