Размах вариации (r)
Размах вариации — это разность между максимальным и минимальным значениями признака
Он показывает пределы, в которых изменяется величина признака в изучаемой совокупности.
Пример
Опыт работы у пяти претендентов на предшествующей работе составляет: 2,3,4,7 и 9 лет.
Решение: размах вариации = 9 — 2 = 7 лет.
Для обобщенной
характеристики различий в значениях
признака вычисляют средние показатели
вариации, основанные на учете отклонений
от средней арифметической. За отклонение
от средней принимается разность .
При этом во
избежании превращения в нуль суммы
отклонений вариантов признака от средней
(нулевое свойство средней) приходится
либо не учитывать знаки отклонения, то
есть брать эту сумму по модулю
, либо возводить значения отклонений в
квадрат
Среднее линейное и квадратическое отклонение
Среднее
линейное отклонение
— это средняя арифметическая из
абсолютных отклонений отдельных значений
признака от средней.
Среднее линейное отклонение простое:
Опыт работы у пяти претендентов на предшествующей работе составляет: 2,3,4,7 и 9 лет.
В нашем
примере:
лет;
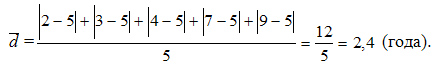
Ответ: 2,4 года.
Среднее линейное отклонение взвешенное применяется для сгруппированных данных:
Среднее линейное отклонение в силу его условности применяется на практике сравнительно редко (в частности, для характеристики выполнения договорных обязательств по равномерности поставки; в анализе качества продукции с учетом технологических особенностей производства).
Среднее квадратическое отклонение
Наиболее
совершенной характеристикой вариации
является среднее квадратическое
откложение, которое называют стандартом
(или стандартным отклонение). Среднее
квадратическое отклонение (
)
равно квадратному корню из среднего
квадрата отклонений отдельных значений
признака от средней арифметической:
Среднее квадратическое отклонение простое:
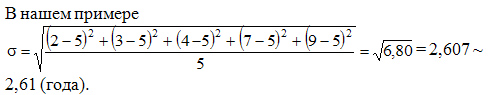
Среднее квадратическое отклонение взвешенное применяется для сгруппированных данных:
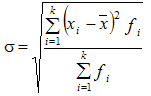
Между средним квадратическим и средним линейным отклонениями в условиях нормального распределения имеет место следующее соотношение: ~ 1,25.
Среднее квадратическое отклонение, являясь основной абсолютной мерой вариации, используется при определении значений ординат кривой нормального распределения, в расчетах, связанных с организацией выборочного наблюдения и установлением точности выборочных характеристик, а также при оценке границ вариации признака в однородной совокупности.
Дисперсия
Дисперсия
- представляет собой средний квадрат
отклонений индивидуальных значений
признака от их средней величины.
Дисперсия простая:
В нашем
примере:
Дисперсия взвешенная:
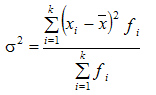
Более удобно вычислять дисперсию по формуле:
которая получается из основной путем несложных преобразований. В этом случае средний квадрат отклонений равен средней из квадратов значений признака минус квадрат средней.
Для несгрупиированных данных:
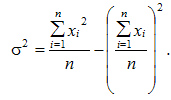
Для сгруппированных данных:
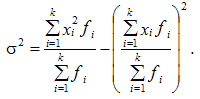
Вариация альтернативного
признака заключается в наличии или
отсутствии изучаемого свойства у единиц
совокупности. Количественно вариация
альтернативного признака выражается
двумя значениями: наличие у единицы
изучаемого свойства обозначается
единицей (1), а его отсутствие — нулем
(0). Долю единиц, обладающих изучаемым
признаком, обозначают буквой
, а долю единиц, не обладающих этим
признаком — через
. Учитывая, что p + q = 1 (отсюда q = 1 — p), а
среднее значение альтернативного
признака равно
средний квадрат отклонений
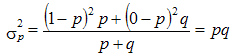
Таким образом, дисперсия альтернативного признака равна произведению доли единиц, обладающих данным свойством ( ),на долю единиц, данным свойством не обладающих ( )
Максимальное значение
средний квадрат отклонения (дисперсия)
принимает в случае равенства долей,
т.е. когда
т.е.
Нижняя граница этого показателя равна
нулю, что соответствует ситуации, при
которой в совокупности отсутствует
вариация. Среднее квадратическое
отклонение альтернативного признака:
Так, если в изготовленной
партии 3% изделий оказались нестандартными,
то дисперсия доли нестандартных изделий
, а среднее квадратическое отклонение
или 17,1%.
Среднее квадратическое
отклонение
равно квадратному корню из среднего
квадрата отклонений отдельных значений
признака от средней арифметической.
Пример расчета показателей вариации
На этапе отбора кандидатов для участия в осуществлении сложного проекта фирма объявлила конкурс профессионалов. Распределение претендентов по опыту работы показало средующие результаты:
Вычислим средний производственный опыт работы, лет
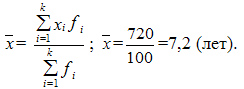
Рассчитаем дисперсию по продолжительности опыта работы
Такой же результат получается, если использовать для расчета другую формулу расчета дисперсии
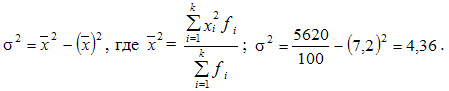
Вычислим среднее
квадратическое отклонение, лет:
Определим коэффициент
вариации, %:
ИНДЕКСНЫЙ МЕТОД-ЗАДАЧА
Рассмотрим сущность индексного метода на конкретном примере. Если анализируемая организация выпускает разнородную продукцию, то рассчитывается общий индекс объема продукции.
Информация об объеме и стоимости выпускаемой продукции.
В рассматриваемом примере мы исчислим аналитические индексы, где в качестве индексируемого признака берется объем выпускаемой продукции, а в качестве весового признака — цена за единицу продукции. На основе данных, приведенных в таблице, рассчитаем общий индекс объема продукции:
На полученный нами результат оказали влияние два фактора:
изменение количества продукции;
изменение цен на продукцию.
Следует отдельно определить:
индекс изменения количества (объема) продукции при условии ее оценки в одинаковых ценах;
индекс изменения цен на продукцию при условии ее одинакового объема.
Вначале найдем индекс изменения количества продукции:
Затем определим индекс изменения цен на продукцию:
В
рассматриваемом примере индекс изменения
количества показывает увеличение объема
продукции на
или на 8 рублей, то есть (123 — 115). Индекс
изменения цен свидетельствует о повышении
цен на продукцию на
, что составляет 10 рублей, то есть (133 —
123).
Если сложить влияние индексов получим общий индекс объема продукции — 18 рублей.
С помощью индексов можно сравнивать данные за ряд лет, например, путем расчетов темпов роста продукции в сопоставимых ценах.
В условиях анализа динамики показателей следует различать понятия цепного и базисного индексов. Базисным называется индекс, рассчитанный по отношению к базисному периоду. Цепным называется индекс, рассчитанный по отношению к предыдущему периоду.
КОРРЕЛЯЦИОННЫЙ МЕТОД-
Показатели корреляции
Параметрические показатели корреляции
Ковариация
Важной характеристикой совместного распределения двух случайных величин является ковариация (или корреляционный момент). Ковариация являетcя совместным центральным моментом второго порядка.[6] Ковариация определяется как математическое ожидание произведения отклонений случайных величин[7]:
где
— математическое ожидание.
КОЭФФИЦИЕНТ КОРРЕЛЯЦИИ и ИНДЕКС КОРРЕЛЯЦИИ
Наиболее распространенный коэффициент корреляции. Предназначен для расчета силы и направления линейной зависимости между переменными исследования.
Смысл коэффициента линейной корреляции.
Коэффициент линейной корреляции отражает меру линейной зависимости между двумя переменными. Предполагается, что переменные измерены в интервальной шкале либо в шкале отношений.Если представить две переменные на координатном поле , то каждая пара значений будет отображать координаты точки в этом поле. Чем ближе точки к усредненной прямой, тем выше коэффициент корреляции Коэффициент корреляции будет положительным числом, когда при повышении X происходит повышение Y (прямопропорциональная связь), отрицательным при обратнопропорциональной связи. На иллюстрации изображены различные по силе положительные коэффициенты корреляции. Индекс корреляции используется для выявления тесноты связи между переменными в случае нелинейной зависимости.
Он показывает тесноту связи между фактором x и зависимой переменной y: . (6.13)
где ei = yi - i - величина ошибки, т.е. отклонение фактических значений зависимой переменной от рассчитанных по уравнению регрессии.
Индекс корреляции есть неотрицательная величина, не превосходящая 1: 0 ≤ Iyx ≤ 1.
Связь тем сильнее, чем ближе Iyx к единице.
В случае линейной зависимости Iyx = | ryx |. Расхождение между Iyx (формула (6.13)) и ryx (формула (6.4)) может быть использовано для проверки линейности корреляционной зависимости.
ЗАДАЧА
Пример 7.1. Результаты наблюдений за характеристиками канала представлены в табл. 7.1.
Необходимо определить наличие линейных корреляционных связей между пропускной способностью и остальными факторами. Предполагается, что выборки по всем вариантам подчиняются нормальному закону. Проверку гипотезы о значимости оценок коэффициентов корреляции произвести с уровнем значимости a , равным 0,1.
Решение. Стандартизация исходной матрицы начинается с вычисления выборочной средней m 1, несмещенной оценки дисперсии m 2 и среднеквадратического отклонения s по каждой варианте, табл.7.2.
Таблица 7.2
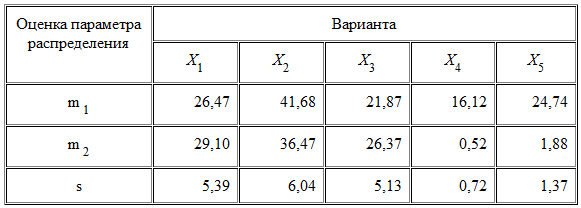
В результате перехода к величинам
формируется стандартизованная матрица
исходных данных, табл. 7.3.
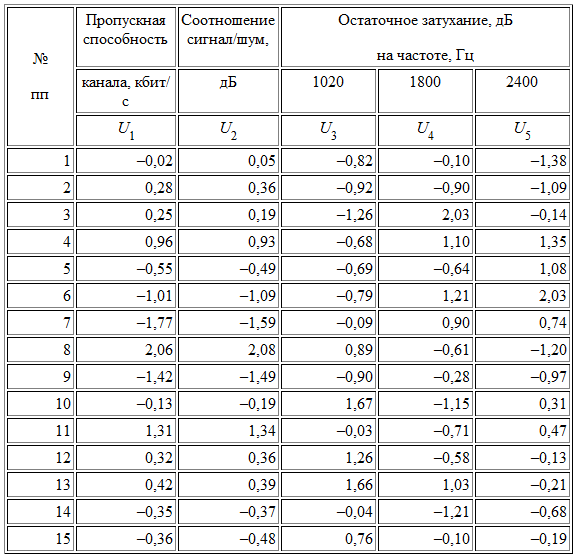
Оценки коэффициентов корреляции
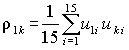(k = 2, 3, 4) представлены в табл. 7.4. В этой
же таблице приведены значения статистик
критерия Стьюдента
для вычисленных оценок коэффициентов
корреляции при п = 15.
Таблица 7.4
Критическое значение tкр (n–2; a ) = tкр (13; 0,1) = 1,77. Статистика критерия больше критического значения только для r 12. Это означает, что только для указанного коэффициента оценка значима (коэффициент корреляции генеральной совокупности не равен нулю), а остальные коэффициенты следует признать равными нулю.
Корреляционная зависимость не обязательно устанавливается только для двух величин, с ее помощью можно анализировать связи между несколькими вариантами (множественная корреляция). А кроме линейной существуют и другие виды корреляции.
ЗАДАЧА 2
Определить форму и направление взаимосвязи между показателями пульса покоя и абсолютными значениями пробы PWC170 у 13 исследуемых с помощью построения графика корреляционного поля, если данные выборок таковы:
xi, уд/мин ~ 80; 72; 71; 80; 84; 82; 78; 70; 83; 72; 72; 73; 81
yi, кГм/мин ~ 858; 979; 1071; 920; 982; 1000; 1004; 1022; 807; 1099; 817; 879; 982
Решение
1. Построим график данного корреляционного поля, отложив на оси Х в порядке возрастания показатели пульса покоя, на оси Y — абсолютные значения пробы PWC170.
2. Сделать вывод о форме и направлении взаимосвязи между исследуемыми показателями.
Вывод: график данного корреляционного поля позволяет предположить, что, возможно, между пульса покоя и абсолютными значениями пробы PWC170 у исследуемой группы наблюдается прямая, обратная зависимость, т.е. со снижением показателя пульса покоя происходит увеличение абсолютных значений PWC170.
Всё взято с сайтов
http://be5.biz/ekonomika/s004/toc.htm
http://works.tarefer.ru/75/100059/index.html
http://www.pravo.vuzlib.net/book_z1206_page_14.html
http://vsempomogu.ru/statistika/333-10.html
http://allstats.ru/?cat=81
http://www.grandars.ru/student/statistika/graficheskoe-predstavlenie-dannyh.html
http://revolution.allbest.ru/mathematics/00348449_0.html
http://dvo.sut.ru/libr/opds/i130hod2/7.htm