
- •1. Определение и простейшие свойства векторных пространств
- •2. Лиинейная зависимость векторов
- •3. Линейная выражаемость системы векторов
- •4. Базис векторного пространства
- •5. Размерность и свойства векторного пространства
- •8)Для любого вектора х и любых чисел α,β выполняется равенство
- •6. Координаты вектора
- •7. Ранг системы векторов
- •8. Ранг матрицы
- •9. Теорема о ранге матрицы
- •10. Связь между базисами пространства
- •11. Подпространство. Сумма и пересечение подпространств
- •12. Теорема о размерности суммы и пересечения подпространств
- •13. Прямая сумма подпространств
- •14. Прямое дополнение подпространств
- •15. Критерий совместимости системы линейных уравнений
- •16. Системы линейных однородных уравнений
- •17. Построение системы линейных однородных уравнений по подпространству
- •18. Связь между решениями однородной и неоднородной системы линейных уравнений
- •19. Определение и простейшие св-ва линейных операторов
- •20. Действие с линейными операторами
- •21. Матрица линейного оператора
- •22. Соответствующие действия над операторами и матрицами
- •23. Изоморфизм линейного пространства
- •24. Ранг и диффект линейного оператора
- •25. Изменение матрицы линейного оператора при замене матрицы
- •26. Инвариантное подпространство
- •27. Линейный оператор с клеточно-диагональной матрицей
- •28. Характеристический многочлен
- •29. Собственные вектора линейного оператора
- •30. Жорданова нормальная форма
- •31. .Построение Жордановой нормальной формы с единственным собственным значением
- •32. Алгоритм нахождения нормальной жордановой формы
- •33. Минимальный многочлен
- •34.Теорема Гамильтона-Келли
- •35. Линейная форма
- •36. Билинейный формы
- •37. Квадратичные формы
- •38. Ограничение билинейных и квадратичных форм
- •39. Ортагональные вектора
- •40. Приведение к кононическому виду
- •41. Алгоритм Логранжа
- •42. Нормальный вид квадратичной формы над c и r
- •43. Закон инерции вещественных квадратичных форм
- •44. Знакоопределенная форма
- •45. Критерий Сильвестра
- •46. Эквивалентность квадратичных форм
- •47. Элементарные делители матрицы
- •48. Матрица Фробениуса сопровождающая систему
- •49. Нормальная форма Фробениуса
16. Системы линейных однородных уравнений
Однородной системой линейных уравнении называют систему
![]()
у которой все свободные члены уравнений равны нулю.
Теорема 16.1 Для того чтобы однородная система линейных уравнений имела единственное решение, необходимо и достаточно, чтобы ранг ее матрицы совпадал с количеством неизвестных системы.
Однородная система линейных уравнений имеет бесконечное множество решений тогда и только тогда, когда ранг ее матрицы меньше числа неизвестных.
Теорема 16.2 Если ранг матрицы А однородной системы Aх=0 меньше числа неизвестных, т.е. rang(A) = r < n, то размерность линейного пространства решений этой системы равна n – r.
Д-во:
Если
ранг rang(A)
= r
< n,
то из n
неизвестных r
являются главными, а n
– r
– свободными. В качестве свободных
выбраны неизвестные ![]() . Возьмем произвольный ненулевой
определитель d
порядка n
– r:
. Возьмем произвольный ненулевой
определитель d
порядка n
– r:
d=![]()
В результате n – r решений однородной системы Aх=0 получим:
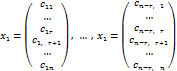
из столбцов ставим матрицу
M=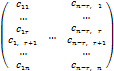 .
Следовательно, все столбцы матрицы,
линейно независимы.
.
Следовательно, все столбцы матрицы,
линейно независимы.
Покажем,
что любое решение ![]() системы Aх=0
линейно выражается через решения
системы Aх=0
линейно выражается через решения ![]() .
.
Рассмотрим столбцы
![]()
столбец
![]() =
= ![]()
Пусть
![]()
Рассмотрим
n-мерный
вектор y
= ![]() =0
=0
у
имеют нулевые значения. Тогда ![]() т.е. произвольно взятое решение х системы
Aх=0
линейно выражается через решения
.
т.е. произвольно взятое решение х системы
Aх=0
линейно выражается через решения
.
Теорема 16.3 Пусть – фундаментальная система решений однородной системы Aх=0 тогда и только тогда, когда он может быть продставлен в виде
![]() ,
где
,
где ![]() – некоторые постоянные.
– некоторые постоянные.
17. Построение системы линейных однородных уравнений по подпространству
18. Связь между решениями однородной и неоднородной системы линейных уравнений
Теорема
18.1
Сумма любого решения ![]() неоднородной системы Ах=b
и любого решения
неоднородной системы Ах=b
и любого решения ![]() приведенной однородной системы Ax=0
является решением неоднородной системы
Ax=b.
приведенной однородной системы Ax=0
является решением неоднородной системы
Ax=b.
Д-во.
В силу равенств A =b и A =0 заключаем, что
A![]() = A
+ A
= b
+ 0 = b,
= A
+ A
= b
+ 0 = b,
это
означает, что столбец ![]() является решением неоднородной системы
Ax=b.
является решением неоднородной системы
Ax=b.
Теорема
18.2
Разность ![]() любых двух решений
любых двух решений ![]() и
неоднородной системы Ах=b
является решением ее приведенной системы
Ax=0.
и
неоднородной системы Ах=b
является решением ее приведенной системы
Ax=0.
Д-во.
В силу равенств A =b и A =b заключаем, что
A![]() = A
- A
= b
- b
= 0,
= A
- A
= b
- b
= 0,
это означает, что столбец является решением однородной системы Ax=0.
Теорема
18.3
Общее уравнение неоднородной системы
Ах=b
можно представить формулой ![]() =
= ![]() , где
, где ![]() – общее решение приведенной системы
Ax=0,
а
– общее решение приведенной системы
Ax=0,
а ![]() – какое-либо частное решение неоднородной
системы Ах=b.
– какое-либо частное решение неоднородной
системы Ах=b.
Д-во.
В силу теоремы 18.1 любой вектор x, имеющий представление
= , является решением неоднородной системы Ах=b. Пусть x – произвольное решение системы Ах=b. Тогда по теореме 18.2 вектор у = х – х0 и потому х содержится в множестве решений, определяемых формулой = .
Пример.
= (2,0,-1,0) системы
![]() найти общее уравнение этой системы
найти общее уравнение этой системы
Решение.
Решая эту систему, получаем общее решение в виде
=
![]() =
= ![]() +
+ ![]()
теперь можем записать общее уравнение неоднородной системы
=
=
+
+ ![]()
19. Определение и простейшие св-ва линейных операторов
Пусть
даны линейные пространства X
и Y
над одним и тем же полем P.
Говорят, что из
пространства
X
в
пространство
Y
действует
оператор
![]() ,
если каждому вектору а из Х по какому-либо
правилу ставится в соответствие
определенный вектор а1=
(а) =
а из Y.
Вектор а1
образом
вектора
а, вектор а – прообразом
вектора
а1
при отображении
.
,
если каждому вектору а из Х по какому-либо
правилу ставится в соответствие
определенный вектор а1=
(а) =
а из Y.
Вектор а1
образом
вектора
а, вектор а – прообразом
вектора
а1
при отображении
.
Оператор действующий из из X в Y, называют линейным, если он сумму любых векторов a и b из Х переводит в сумму их образов а1 и b1, а произведение любого вектора а из Х на любое число из P – в произведение образа а1 вектора а на то же число , т.е. если
![]() =
= ![]() +
+ ![]() = а1
+
b1,
= а1
+
b1,
![]() =
= ![]() =
= ![]() а1
а1
Из определения линейного оператора вытекают следующие утверждения:
1) линейный оператор приводит линейную комбинацию векторов
![]() из Х в линейную комбинацию образов
из Х в линейную комбинацию образов ![]() этих векторов с теми же коэффициентами,
т.е.
этих векторов с теми же коэффициентами,
т.е.
![]() =
= ![]()
2)
линейный
оператор ![]() переводит
нулевой вектор 0 из Х в нулевой вектор
01
из Y
переводит
нулевой вектор 0 из Х в нулевой вектор
01
из Y
Д-во:
![]()
3) линейный оператор переводит вектор –а, противоположеный вектору а, в вектор –а1, противоположный вектору а1= a
Д-во:
![]()
Теорема
19.1. Пусть
линейный оператор
действует
из линейного пространства Х в линейное
пространство Y
и ![]() –
базис в Х.
–
базис в Х.
Тогда
оператор
определяется с заданием образов ![]() векторов базиса
.
векторов базиса
.
