1.16. Оптические компрессоры. Призменный компрессор.

Призменный компрессор (ПК) состоит из четырех одинаковы призм. При этом призмы должны располагаться следующим образом. В первой паре призм грани призм должны быть параллельны друг другу, а соответственно симметрично к первой паре линз, что и иллюстрирует рисунок 25. Для такого компрессора мы записали выражение для дисперсионного параметра и для параметра . ПК в отличие от РК могут обладать как положительным значительным дисперсии так и аномальным значением дисперсии. При этом величину коэффициента можно подбирать за счет выбора материала призм, т.е. подбором зависимостей производных показателя преломления по длины волны. Также за счет изменения угла , которое достигается за счет перемещения второй призмы по отношению к первой по вертикальной оси. Т.о. изменяя эти параметры, можно добиться того, что компрессор будет обладать нужным значением коэффициента . 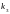Отличительной особенностью ПК от РК является то, что они обладают разным знаком коэффициента , который в свою очередь описывает дисперсию коэффициента . Т.е. зачастую становится важно то, какая величина коэффициента у компрессии, с помощью данной величины можно попытаться компенсировать дисперсию третьего порядка в одномодовом волокне.

1.17. Оптические компрессоры. Чирпированные зеркала.

Следующий тип компрессора – это чирпированные зеркала. Они представляют собой диэлектрическое зеркало с переменной толщиной диэлектрических слоев. Из-за разнотолщинности разные спектральные компоненты отражаются от разных слоев зеркала. Т.е. при отражении подразумевается эффективное отражение ,которое имеет место при резонансном отражении. То же самое, что и выполнение условия резонанса для интерферометра. В итоге получается так как разная спектральные компоненты отражаются от разных слоев, то получается, что время задержки будет зависеть от длины волны, и соответственно данное устройство будет обладать определенным типом и величиной дисперсии. Мы показали, что такие чирпированные зеркала могут обладать и отрицательным значением коэффициента , т.е. обладать аномальной дисперсией.

1.18. Схема компрессии лазерных импульсов.

Далее мы рассмотрели принципиальную схему ВО компрессии, которая заключается в следующем: на вход волоконного световода подается ЛИ, далее в волоконном световоде ЛИ приобретает нелинено-частотную модуляцию и поступает на вход компрессора, который обладает аномальной дисперсией. В результате после прохождения такого компрессора длительность ЛИ уменьшается. В реальном случае в волоконном световоде помимо явления фазовой самомодуляции (ФСМ) есть также и явления, связанные с дисперсионным расплыванием. Т.е. необходимо одновременно учитывать и ФСМ, и дисперсионное расплывание. Для учета этих двух явлений одновременно используется нелинейное уравнение Шредингера, которое можно решить только численно. Трансформацую ЛИ на основе решения нелинейного уравнения Шредингера приведена на рисунке 29. Из данного рисунка видно, что форму ЛИ, который изначально является Гауссовским, при распространении в волоконном световоде изменяется. Т.е. на расстоянии 2 длин ЛИ становится практически прямоугольным.