§19. Формула Симпсона (парабол).

y B C A -h O h x

Рассмотрим точки A(-h, y-1), B(0, y0), C(h, y1). Уравнение параболы, проходящей через эти точки: y=a+bx+cx2 (1)

Площадь параболы, проходящей через точки A, B, и С вычисляется по формуле: (2).

Из (1), сложив первое и третье равенства, найдём: откуда 2ch²=y_-1-2y₀+y₁ и тогда .

Рассмотрим теперь функцию y=f(x), заданную на [a, b]. Требуется вычислить Разобьём отрезок [a, b] на 2n отрезков a=x₀<x₁<…<x_2n=b. Заменим дугу кривой y=f(x) ( ) параболой, проходящей через эти точки и тогда

y C B A y0 y1 y2 O a=x0 x1 x2 b=x2n x

площадь криволинейной трапеции, ограниченной сверху параболой, будет вычисляться по формуле: . Вычислим площадь следующей криволинейной трапеции на [x2, x4]: и так далее. Искомая площадь будет приближённо равна:

Оценка погрешности для формулы Симпсона (без вывода):

Пример 1. Найти приближённое значение интеграла с помощью квадратурных формул прямоугольников, трапеций и Симпсона, если отрезок [0, 1] разбит на 10 равных частей.

Решение:

.

При n=10 получим следующие оценки величин погрешности результатов:

Пример 2. Вычислить интеграл . по формуле Симпсона.

Решение: Возьмём .

.Тогда .

§20. Приемы приближенного вычисления несобственных интегралов.

Рассмотрим интегралы вида:

(1), (2), (3).

Для случая (3) функция f(x) имеет бесконечный разрыв либо в точке x=a, либо x=b, либо x=cÎ[a, b]. Вычисляемые несобственные интегралы при этом предполагаются сходящимися.

Одним из источников получения численных значений несобственных интегралов (1) и (2) являются квадратурные формулы вида: (Гаусса-Кристоффеля). Для их применения нужно выделить под интегралом подходящую весовую функцию и воспользоваться соответствующей квадратурой.

Тогда для интеграла (1): - формула Лагерра, где , L_n-1- n-1-ый многочлен Лагерра.

Аналогично, для интеграла (2) имеем: 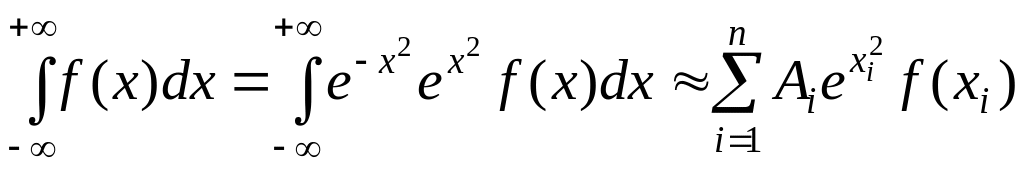- формула Эрмита, где , H_n-1- n-1-вый многочлен Эрмита.

К вычислению интегралов с бесконечной верхней границей можно применять различные формулы численного интегрирования, пользуясь равенством, определяющим несобственный интеграл: . Оно позволяет считать, что для достаточно больших значений b выполняется и вычислять интеграл с помощью известных квадратурных правил. предполагая исходный интеграл абсолютно сходящимся, величину абсолютной погрешности, то есть , за счет увеличения b можно сделать как угодно малой.

В случае (2) без ограничения общности можно считать, что подынтегральная функция имеет особенность на границе промежутка интегрирования, то есть если точкой c, где f(x) обращается в бесконечность, окажется внутренняя точка интервала (a, b), то данный интеграл можно представить символически как . Также без потери общности, достаточно рассматривать . Но к таким интегралам, в которых подынтегральная функция имеет особыми точками значения -1 и (или) 1, можно применить квадратурную формулу Эрмита (Мелера) в виде = или более общую формулу, где параметры a > -1, b > -1 желательно подобрать так, чтобы функция была как можно более гладкой. Такой прием при вычислении несобственных интегралов называют мультипликативным выделением особенностей. Существует несколько специальных квадратурных формул, позволяющих "загнать" в весовые функции различные типы особенностей: степенную, логарифмическую и другие.

Применяются и другие приемы вычисления несобственных интегралов. Надо отметить, что иногда достаточно сделать удачную замену переменной, чтобы преобразовать несобственный интеграл к более подходящему для вычисления виду.