Численное интегрирование.

Для приближённого вычисления определённого интеграла разобьём отрезок интегрирования [a, b] на n равных частей точками x₀=a, x₁₌x₀+h,…, x_i+1=x_i+h,…,x_n=b

(h - шаг разбиения, ).Значения функции f(x) в точках разбиения x_i обозначим y_i. Непрерывная подинтегральная функция y=f(x) заменяется сплайном (кусочно-полиномиальной функцией) S(x), аппроксимирующей данную функцию. Интегрируя функцию на отрезке [a, b], придём к некоторой формуле численного интегрирования (квадратурной формуле).

В зависимости от функции S(x), аппроксимирующей подинтегральную функцию, будем получать различные квадратурные формулы.

§17. Формула прямоугольников.

Если на каждой части [x_i-1, x_i], i= деления отрезка [a, b] функцию f(x) заменить функцией, принимающей постоянное значение, равное, например, значению функции f(x) в серединной точке i-й части, то есть 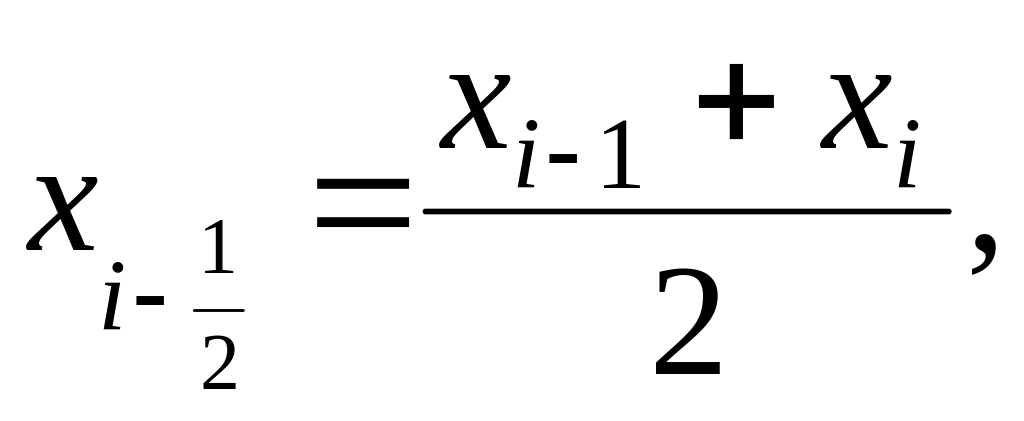то функция S(x) будет иметь ступенчатый вид:

.

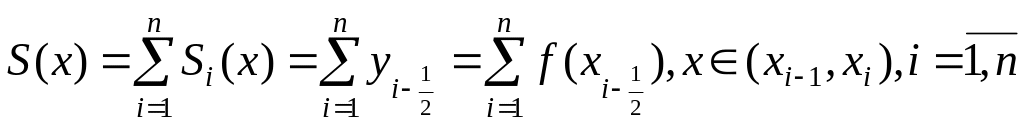В этом случае 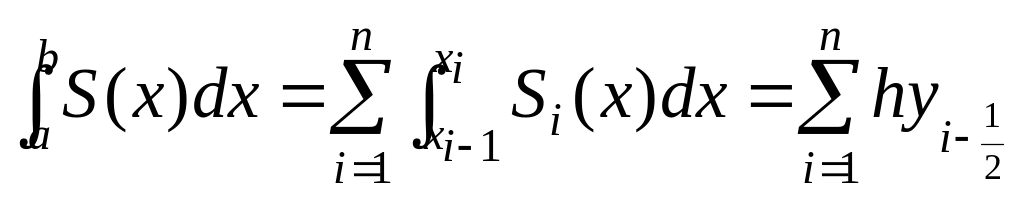и получаем квадратурную формулу прямоугольников

(1).

Пример. Найти приближённое значение интеграла по формуле прямоугольников.

Решение. Пусть n=10.Тогда x₀=0, …, x₁₀=1.

,

=

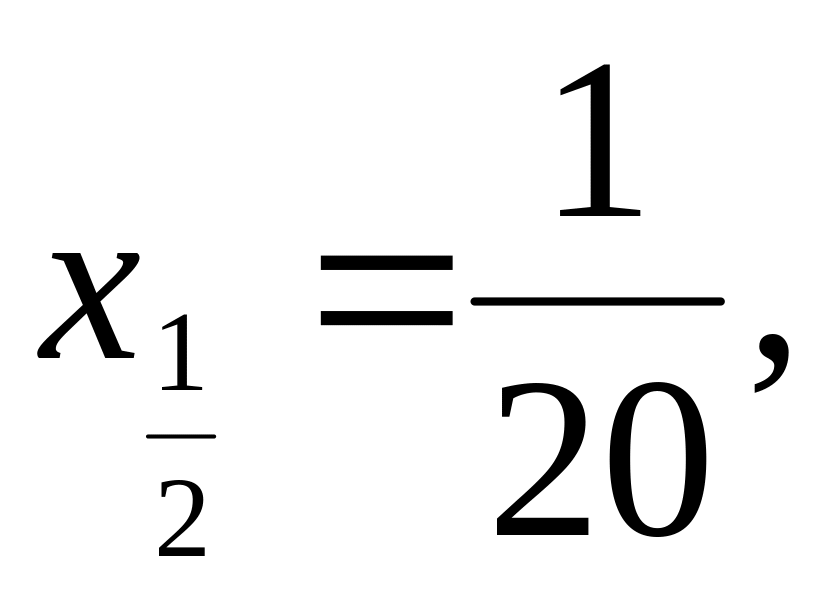
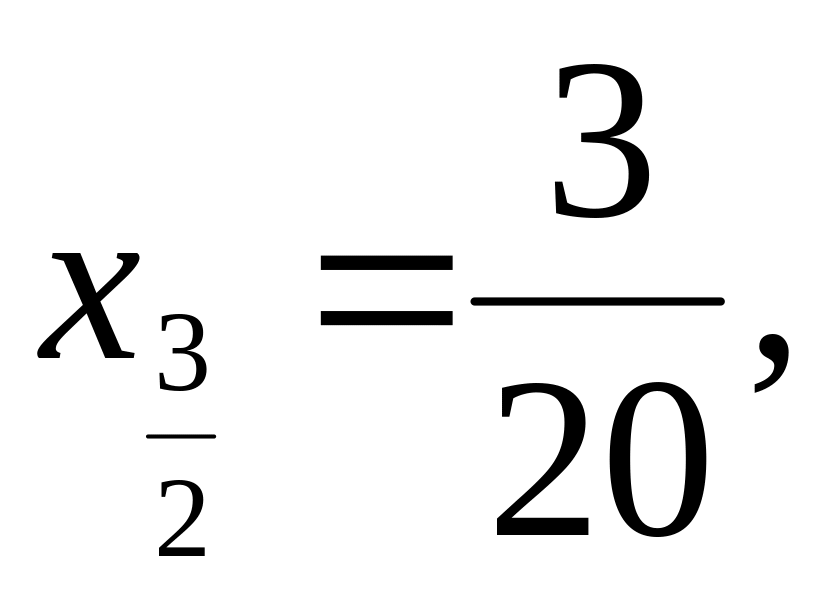
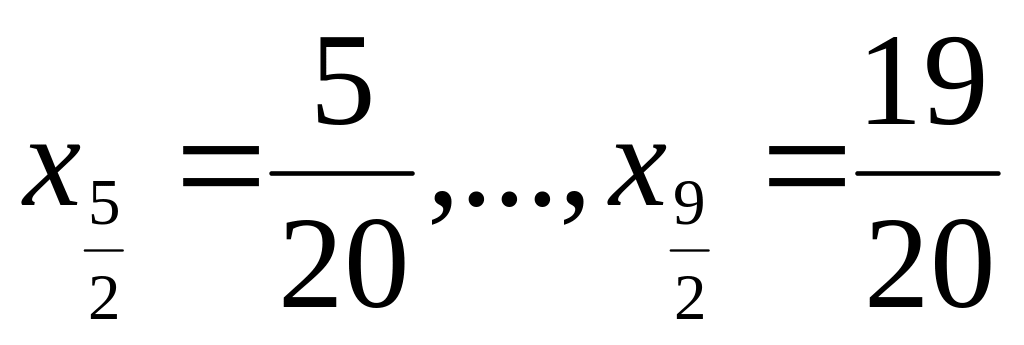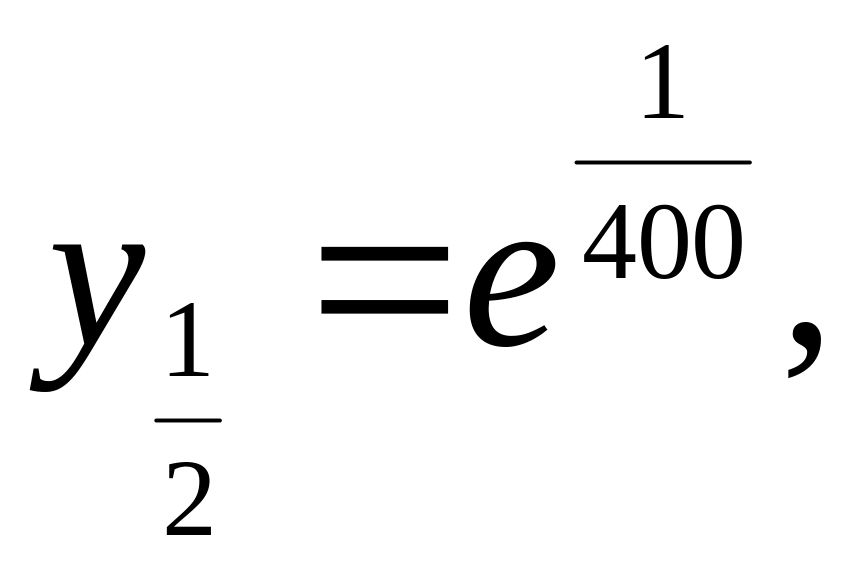
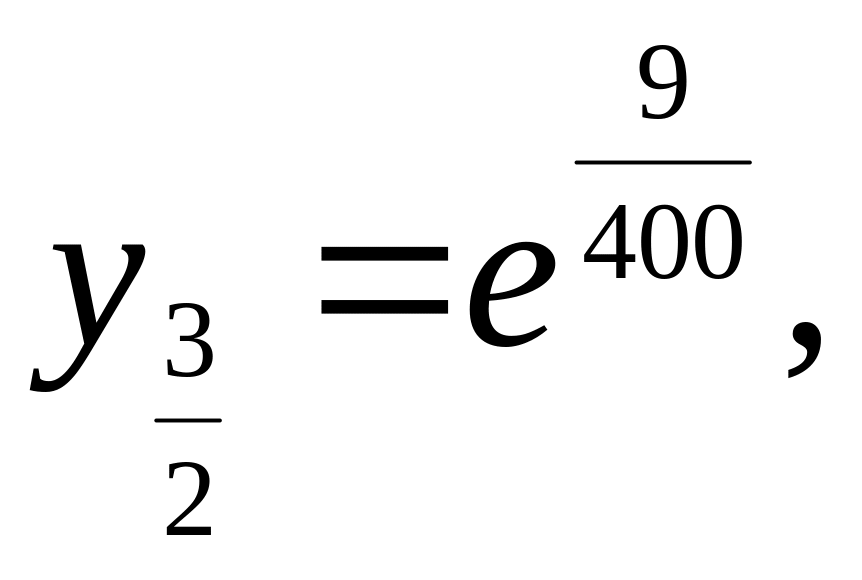
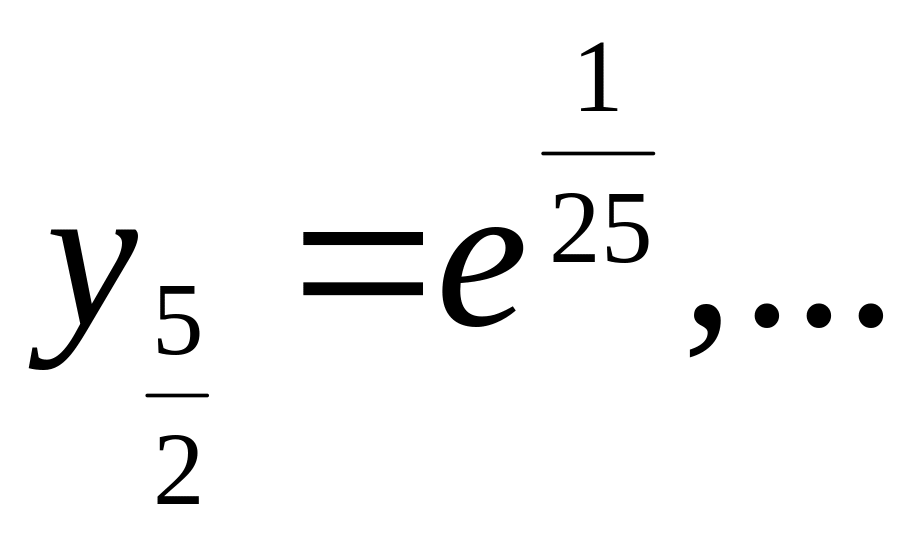
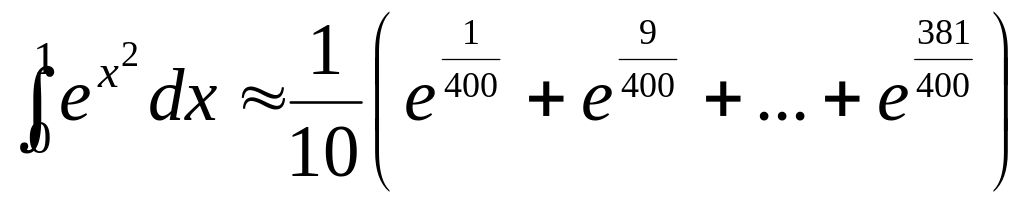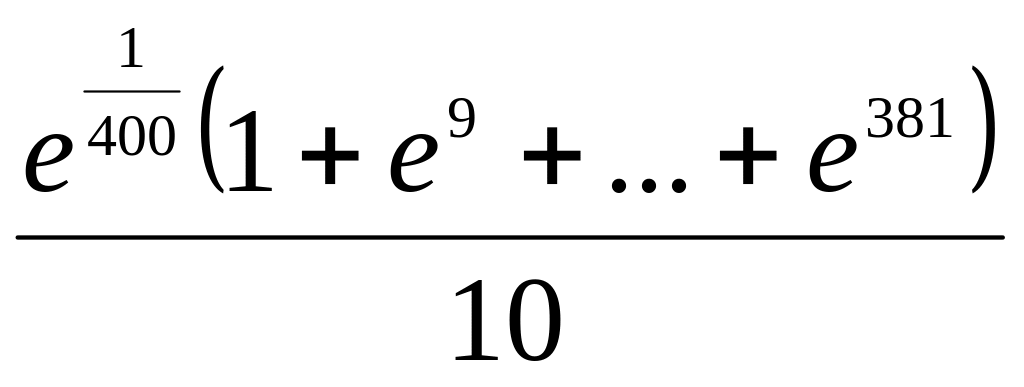
Погрешность квадратурной формулы оценивается величиной остаточного члена R(h), зависящего от шага разбиения h (или от числа разбиений n).

y f(0) f(h) O a b x

На одном (первом) отрезке разбиения имеем: где 0£с£h. Если то проинтегрируем неравенство на отрезке [0, h]:

Но легко заметить, что тогда откуда (переходя от h к x) получим: , где 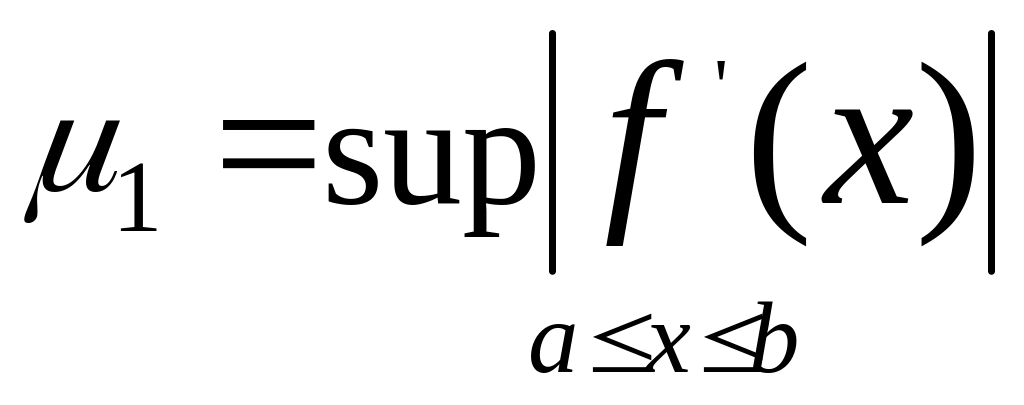, то есть, уже на всем отрезке [a, b]. Таким образом получаем общую погрешность на [a, b]

(так как hn= b - a).

§18. Формула трапеций.

Если функцию f(x) на каждом отрезке [x_i-1, x_i] заменить её линейной интерполяцией по точкам (x_i-1,y_i-1),(x_i, y_i) то получим непрерывную кусочно-линейную функцию

.

Здесь y_i=f(x_i). Графиком этой функции является ломаная линия. В этом случае

и получаем квадратурную формулу трапеций: таким образом:

(1).

y f(0) f(h) O a b x

Оценка погрешности этой формулы:

где , а тогда а общая погрешность на [a, b] тогда равна .