
- •Расчетно-графическая работа №2
- •Содержание
- •Задание
- •Определение основных параметров привода и выбор электродвигателя
- •2. Выбор материалов и расчёт допускаемых напряжений
- •2.1 Выбор материалов для изготовления деталей редуктора
- •2.2 Определение допускаемого контактного напряжения
- •3. Определение основных геометрических параметров зубчатой передачи
- •3.1 Расчёт межосевого расстояния
- •3.2 Определение геометрических параметров зубчатых колёс
- •4. Проверочный расчёт на прочность зубчатой передачи по контактным напряжениям
- •5. Расчёт валов и корпуса редуктора. Выбор подшипников
- •Литература
3.2 Определение геометрических параметров зубчатых колёс
Ширину колеса определяем по формуле bw2= Ψba ∙ aw= 0,3 ∙200=60 мм.
По ряду Rа40 принимаем bw2=60
Ширина шестерни должна быть на 3..5мм больше ширины колеса:
bw1= bw2+4= 64 мм.
Нормальный модуль зацепления принимаем в пределах:
mн= ( 0,01…0,02 ) ∙aw= ( 0,01…0,02) ∙200= 2,0…4,0 мм.
Принимаем стандартный модуль зацепления mн = 2 мм.
При
определении оптимального угла наклона
зуба учитываем, что коэффициент осевого
перекрытия должен соответствовать
следующему условию:
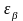 >
1,1. Предварительно принимаем
=
1,6.
>
1,1. Предварительно принимаем
=
1,6.
Угол
наклона зуба должен быть в пределах
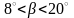 .
.
Угол наклона зуба определяется по формуле
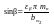 ,
,
Тогда
угол наклона зуба
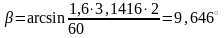 .
.
 Суммарное
число зубьев шестерни и колеса определяется
по формуле
Суммарное
число зубьев шестерни и колеса определяется
по формуле
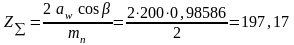 .
.
Принимаем
целое число
 .
.
Число
зубьев шестерни
 .
Необходимо учитывать, что по условию
неподрезания зубьев
.
Необходимо учитывать, что по условию
неподрезания зубьев
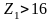 .
Принимаем
.
Принимаем
 .
.
Число
зубьев колеса.

Уточняем
передаточное отношение:
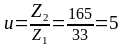 .
.
Определяем
процент расхождения:
 .
Допускается расхождение не более 4 %.
.
Допускается расхождение не более 4 %.
Фактическая
частота вращения ведомого (выходного)
вала редуктора
 об/мин.
об/мин.
Отклонение действительной частоты вращения ведомого вала от заданной не должно превышать 4 %.

Уточняем величину угла наклона зуба:

 ,
,
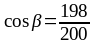 .
.
Делительные диаметры шестерни и колеса:
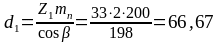 мм. Принимем d1=
60 мм,
мм. Принимем d1=
60 мм,
;
 мм. Принимем d2= 340
мм,
мм. Принимем d2= 340
мм,
Проверка:
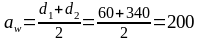 мм.
мм.
Диаметры окружностей выступов шестерни и колеса:
 мм;
мм;
 мм.
мм.
Диаметры окружностей впадин шестерни и колеса:
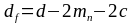 ,
где с – радиальный зазор,
,
где с – радиальный зазор,
 ,
мм.
,
мм.
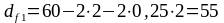 мм,
мм,
 мм.
мм.
4. Проверочный расчёт на прочность зубчатой передачи по контактным напряжениям
 Условие
прочности зубчатой передачи по контактным
напряжениям:
Условие
прочности зубчатой передачи по контактным
напряжениям:
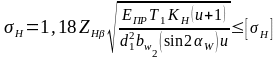 ,
,
где
 – коэффициент, учитывающий повышение
прочности косозубых передач по контактным
напряжениям;
– коэффициент, учитывающий повышение
прочности косозубых передач по контактным
напряжениям;
 – стандартный
угол зацепления,
– стандартный
угол зацепления,
 ;
;
 –
коэффициент
расчетной нагрузки. Определяется по
формуле
–
коэффициент
расчетной нагрузки. Определяется по
формуле
=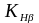
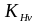 ,
где
– определенный ранее коэффициент
концентрации напряжений,
– коэффициент, учитывающий динамический
характер приложения нагрузки. Определяется
коэффициент динамической нагрузки
по графику в зависимости от окружной
скорости и назначенного квалитета
точности изготовления передачи.
,
где
– определенный ранее коэффициент
концентрации напряжений,
– коэффициент, учитывающий динамический
характер приложения нагрузки. Определяется
коэффициент динамической нагрузки
по графику в зависимости от окружной
скорости и назначенного квалитета
точности изготовления передачи.
Коэффициент
 ,
учитывающий повышение прочности
косозубых передач по контактным
напряжениям, определяется по формуле
,
учитывающий повышение прочности
косозубых передач по контактным
напряжениям, определяется по формуле
 ,
,
где
 –
коэффициент, учитывающий неравномерность
нагрузки одновременно зацепляющихся
пар зубьев.
–
коэффициент, учитывающий неравномерность
нагрузки одновременно зацепляющихся
пар зубьев.
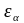 –
коэффициент
торцового перекрытия.
–
коэффициент
торцового перекрытия.
Коэффициент
торцового перекрытия
 определяется по формуле:
определяется по формуле:
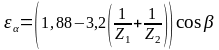 ,
,
Значение
коэффициента
зависит от величины окружной скорости
и назначенной степени точности (квалитета)
изготовления передачи. Окружная скорость
определяется по формуле
 .
.
Степень
точности назначается при помощи таблицы
зависимости квалитета от величины
окружной скорости, а коэффициент
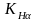 определяется по таблице зависимости
коэффициента, учитывающего неравномерность
нагрузки одновременно зацепляющихся
пар зубьев от величины окружной скорости
и назначенного квалитета .
определяется по таблице зависимости
коэффициента, учитывающего неравномерность
нагрузки одновременно зацепляющихся
пар зубьев от величины окружной скорости
и назначенного квалитета .
Окружная
скорость
 м/с.
м/с.
Назначаем по таблице зависимости квалитета от величины окружной скорости 8 степень точности изготовления передачи. При помощи таблицы зависимости коэффициента, учитывающего неравномерность нагрузки одновременно зацепляющихся пар зубьев от величины окружной скорости и назначенного квалитета определяем коэффициент , зависящий от окружной скорости и назначенной степени точности (квалитета): =1,07.
Коэффициент торцового перекрытия определяем по формуле:
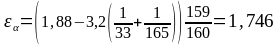 .
.
 Коэффициент,
учитывающий повышение прочности
косозубых передач по контактным
напряжениям определяем по формуле:
Коэффициент,
учитывающий повышение прочности
косозубых передач по контактным
напряжениям определяем по формуле:
 .
.
При помощи графика зависимости коэффициента динамической нагрузки
от окружной скорости и квалитета определяем коэффициент динамической нагрузки.
Для
8 степени точности и
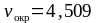 м/с принимаем
=
1,045.
м/с принимаем
=
1,045.
Коэффициент
расчетной нагрузки
=
 .
.
По формуле определяем напряжение, возникающее в линии контакта зубьев, и сравниваем его с допускаемым:

 Па.
Па.
 МПа – условие
прочности по контактным напряжениям
выполняется.
МПа – условие
прочности по контактным напряжениям
выполняется.
Фактическое
напряжение в линии контакта зубьев
 не должно превышать допускаемое более
чем на 4% и не должно быть менее допускаемого
более чем на 20 %.
не должно превышать допускаемое более
чем на 4% и не должно быть менее допускаемого
более чем на 20 %.

