28(1). Опр. И пр. Банах. И гильб. Пространств.

Опр. Множество Х является линейным пространством поля Р, если в пространстве Х определены операции сложения и операции умножения на элементы поля Р.

Аксиомы:

1. Коммутативность ;

2. Ассоциативность ;

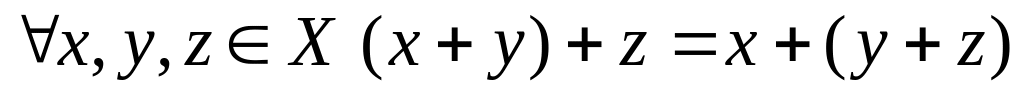3. Существует нулевой элемент в Х: ;

4. ;

5. ;

6. ;

7. ;

8. ;

9. ;

10. .

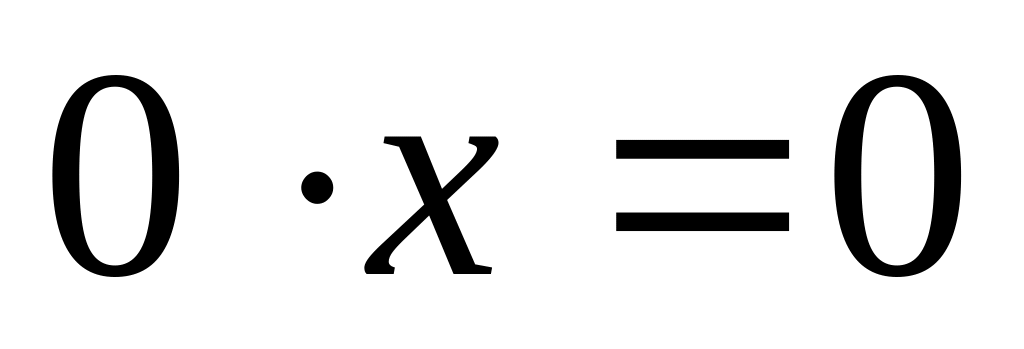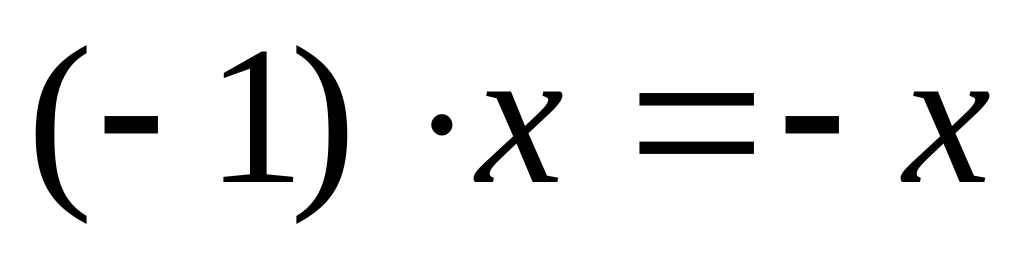Если выполнены аксиомы 1-10, то Х- линейное пространство (в качестве Р возьмем R).

Опр. Пусть Х- линейное пространство заданное отношение. P называется нормой, если это отношение удовлетворяет аксиомам:

1. при этом ,

2. 

3. 

Опр. Если на пространстве Х задана норма, то Х- нормированное пространство.

Пусть последовательность сходится по норме пространства , если .

Опр. , то фундаментальная.

Опр. Если любая фундаментальная последовательность в сходится, то -полное.

Опр. -ограничено, если .

Опр. - линейное пространство - нормы. эквивалентны, если .

Опр. Полные линейные нормированные пространства - Банаховые пространства.

Примеры:

1. (евклидова норма);

2.

3.

;

4. .

Частный случай банаховых пространств- гильбертовы пространства.

Опр. Полное пространство с нормой , где скалярное произведение, обладающее следующими свойствами:

1. - нулевой элемент пространства

2. коммутативность

3.

4. дистрибутивность

называется гильбертовым пространством.

Покажем, что действительно является нормой:

◄1.

2.

3.

Т.о., скалярное произведение порождает норму.

Примеры:

1. гильбертово пространство.

2. не является гильбертовым.

3. , гильбертово пространство

При

4.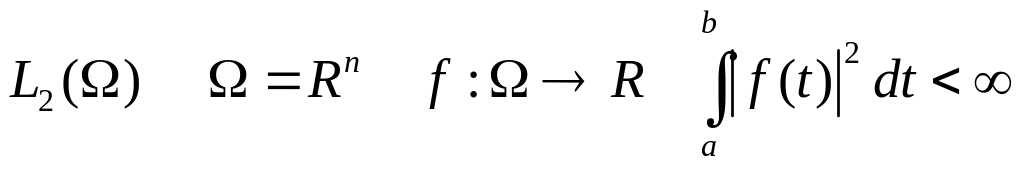 гильбертово пространство

.

29(1). Лиин. Непр. Операторы в норм. Простр.

Опр. Множество Х является линейным пространством поля Р, если в пространстве Х определены операции сложения и операции умножения на элементы поля Р.

Аксиомы:

1. Коммутативность ;

2. Ассоциативность ;

3. Существует нулевой элемент в Х: ;

4. ;

5. ;

6. ; 7. ;

8. ;

9. ;

10. .

Если выполнены аксиомы 1-10, то Х- линейное пространство (в качестве Р возьмем R).

Опр. Пусть Х- линейное пространство заданное отношение. P называется нормой, если это отношение удовлетворяет аксиомам:

1. при этом ,

Опр. Если на пространстве Х задана норма, то Х- нормированное пространство.

Опр. Пусть линейные пространства называется оператором, если область определения .

Опр. Оператор называется линейным, если

1. аддитивность

2. однородность

Пример. Интеграл Лебега – линейный оператор

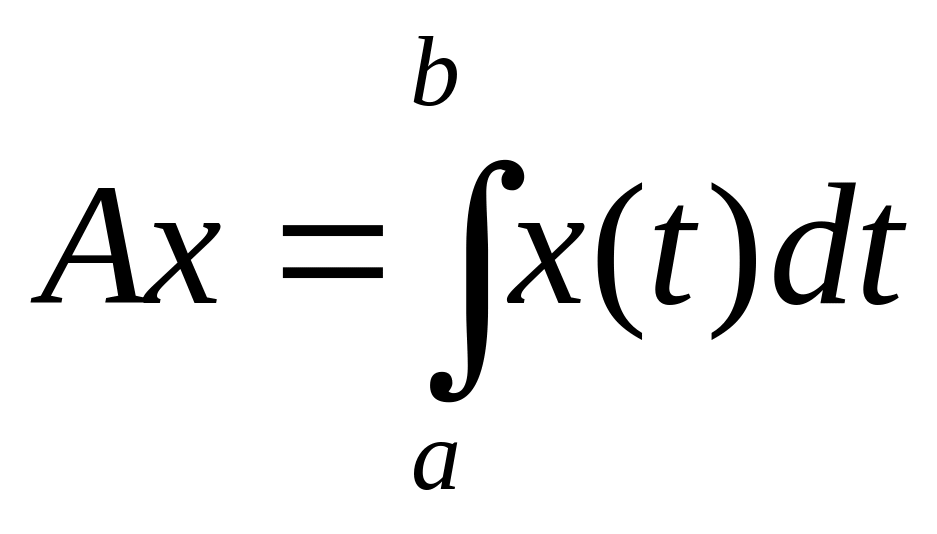
Опр. Говорят, что оператор непрерывен в т. если .

Опр. Оператор непрерывен на множестве, если он непрерывен в каждой точке этого множества

Теорема. Для того, чтобы линейный оператор был непрерывен во всем пространстве необходимо и достаточно, чтобы этот оператор был непрерывен в одной точке пространства .

◄ Если линейный оператор непрерывен во всех точках пространства , то он непрерывен и в одной точке.

Пусть непрерывен в т.

В проверим

Рассмотрим . Пусть непрерывен в т. , покажем что . Рассмотрим ►

Опр. Пусть линейные нормированные пространства . называется ограниченным оператором, если

Теорема. Пусть линейные норм-ые пространства . Для того, чтобы оператор был непрерывным необходимо и достаточно, чтобы он был ограниченным.

◄1) Пусть - непрерывный, докажем, что ограниченный. Предположим, что не является ограниченным отметим что

Рассмотрим последовательность

Рассмотрим последовательность

Оператор А – непрерывен (1)

Рассмотрим

Не стремится к нулю. Последнее неравенство и выражение (1) противоречат друг другу.

2) ограничен. Докажем, что А – непрерывный. Для того, чтобы он был непрерывен во всем пространстве необходимо и достаточно, чтобы он был непрерывен в нуле

.►

Опр. Пусть линейные нормированные пространства - линейный ограниченный оператор. Неравенство ограниченности имеет вид

Опр. Нормой линейного ограниченного оператора называется (минимальная const для которой неравенство ограниченности выполняется), где число, для которого выполняется неравенство ограниченности:

Теорема. Пусть линейные нормированные пространства - линейный ограниченный оператор. Имеет место равенство .