22(1). Длина кривой на пов-ти.

Пусть V: параметризованная пов-ть , l кривая на этой пов-ти заданная уравнением:

Найдем длину этой кривой по формуле:

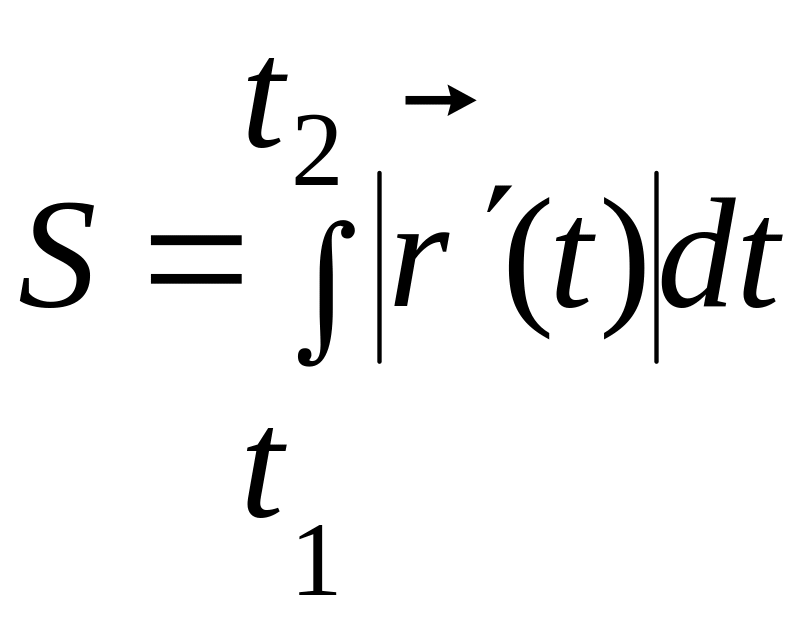
Радиус- вектор кривой l имеет следующий вид: поэтому

и

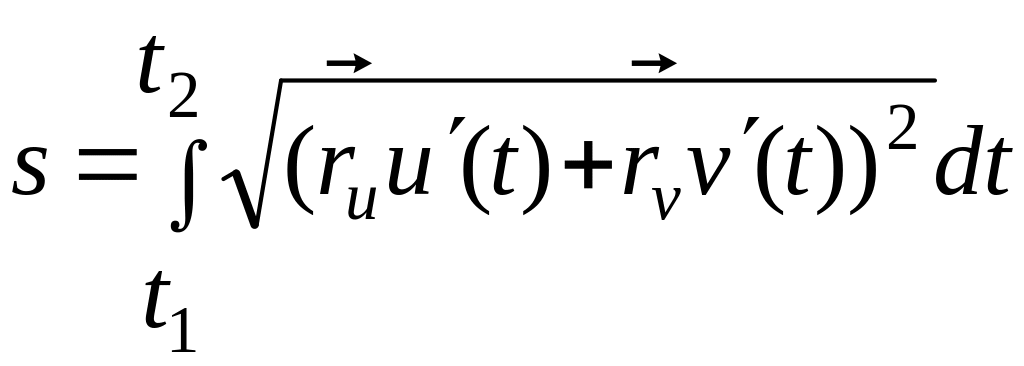
Обозначим , , (1)

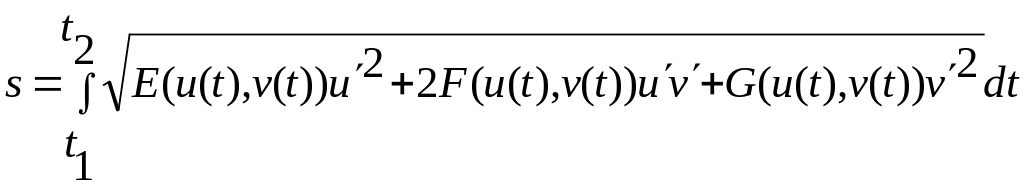тогда (2)

Это равенство можно записать в другом виде

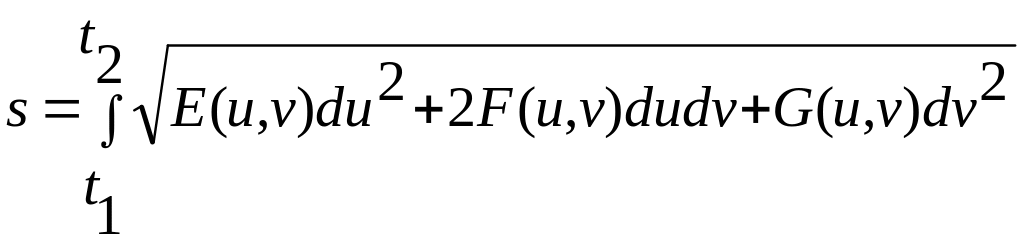(3)

Выражение, стоящее под радикалом в формуле (2) или (3) – представляет собой квадратичную форму относительно производных и наз. первой квадратичной формой пов-ти V. Функции , , наз. коэффициентами первой квадратичной формы. Из равенства (3) следует также формула

Первая квадратичная форма (линейный элемент поверхности) является положительно определенной формулой, поэтому коэффициенты , , удовлетворяют неравенствам: , ,

Найдем линейные эл-ты сферы, пл-ти и цилиндра:

1).Сфера: Парам-кие ур-я сферы:

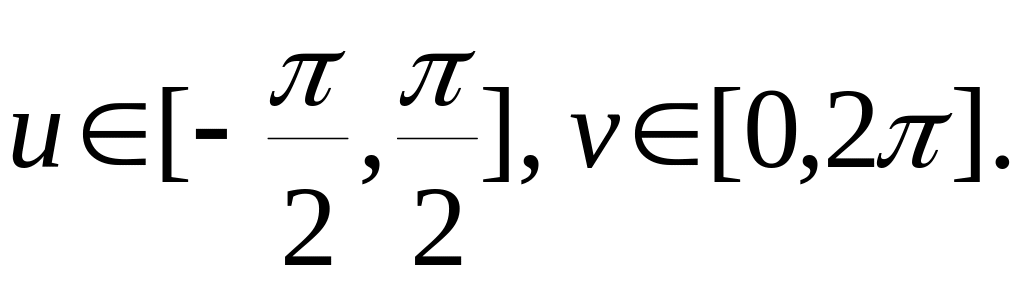
В вект. форме:

Найдем подвижн.базис :

Посчит. коэфф. 1^ой кв.ф.

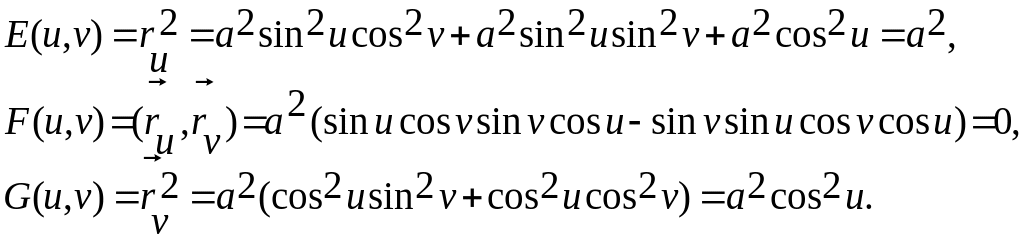
- линейный элемент сферы.

2).Плоскость:Ax+By+Cz+D=0. Запишем в векторной форме: .

- линейный элемент плоскости.

3).Круговой цилиндр: . .

- линейный элемент цилиндра.

23(1). Норм. Кривизна кривой на пов-ти.

Пусть V: параметризованная пов-ть . Пусть кривая задана с помощью натурального параметра

, где - натуральный параметр. Возьмем на кривой регулярную т.М.

единичный вектор на касательной к кривой l. Тогда 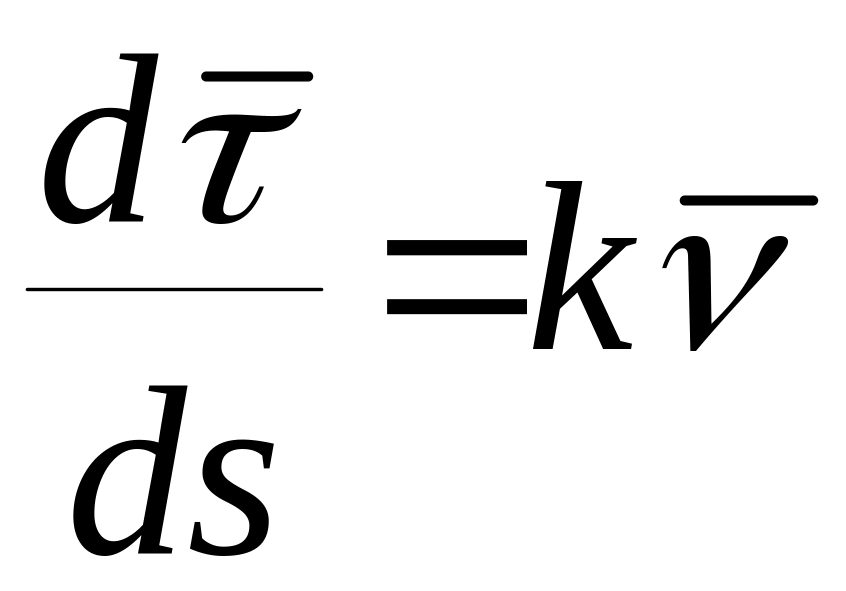- вектор кривизны кривой l, здесь - единичный вектор главной нормали. Рассмотрим проекцию на нормаль и на касательную плоскость.

нормальная кривизна кривой l в т. М на пов-ть V

-геодезическая кривизна.

Посчитаем теперь нормальную кривизну. Пусть кривая l задана ур-ем

, где s натур-ый параметр.

- радиус-вектор кривой.

, где , ,

(2)

.

.

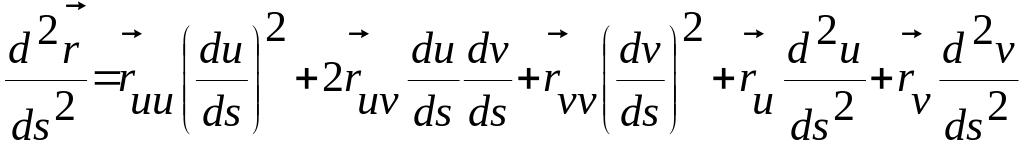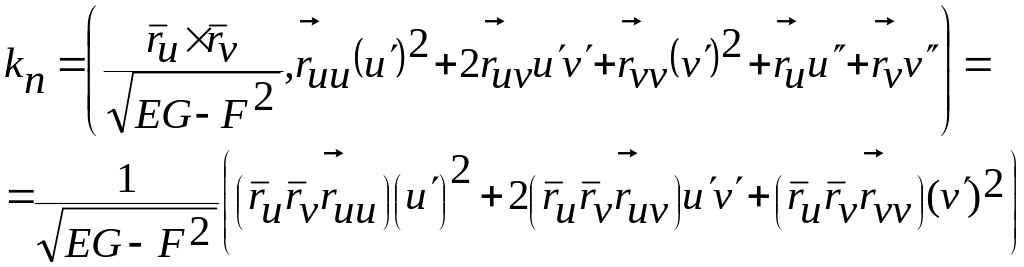Обозначим

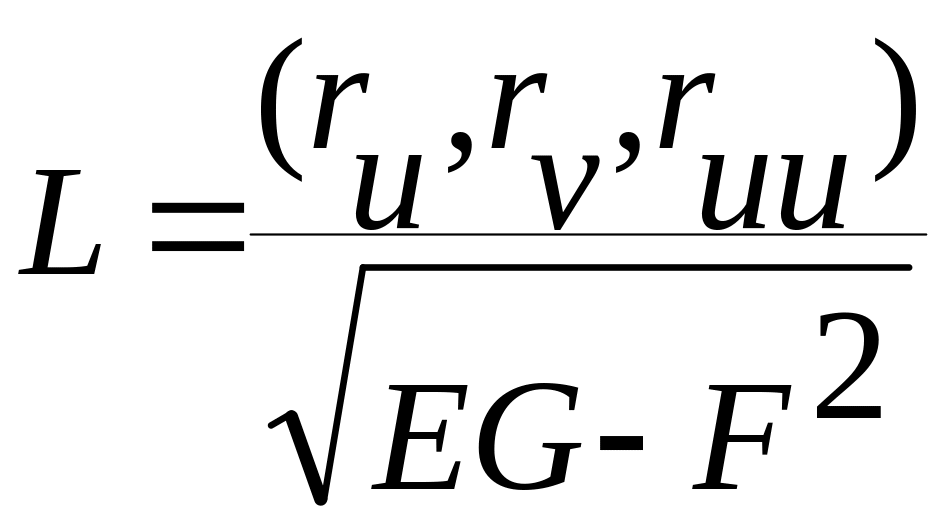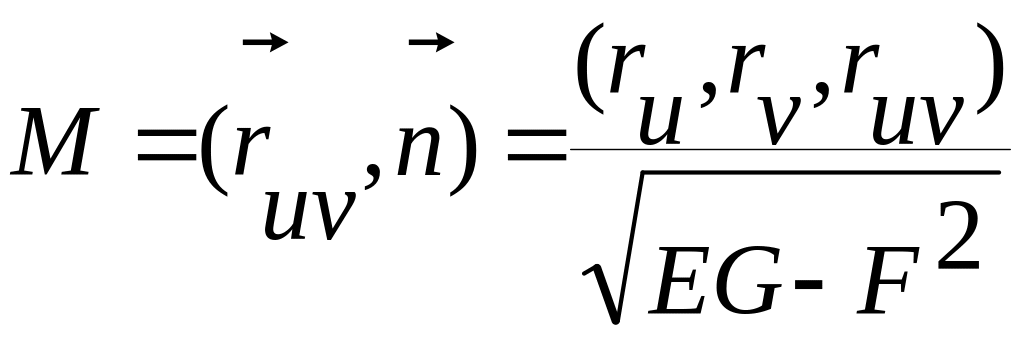, , . (3)

L, M, N – коэфф-ты 2^ой квадратичной формы.

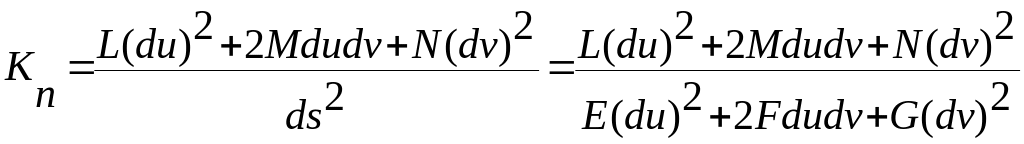(4) Выражение, в числителе представляет собой кв.ф. относительно и наз. второй кв. формой пов-ти. Т.о., нормальная кривизна пов-ти равна отношению 2^ойкв.ф. к 1^ойкв.ф. = - 2^ая кв.ф. пов-ти.

У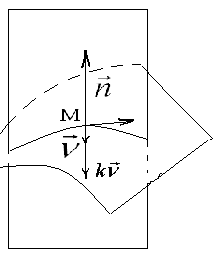 тв. Если две кривые, лежащие на пов-ти, касаются друг друга в т.М, то в т.М нормальная кривизна у них одинакова.

Для этого достаточно посмотреть на ф-лу (4). В неё входят L, M, N, E, F, G, значения кот. вычислены в т.М. Для обеих кривых т.М одна и та же. Еще в (4) входят 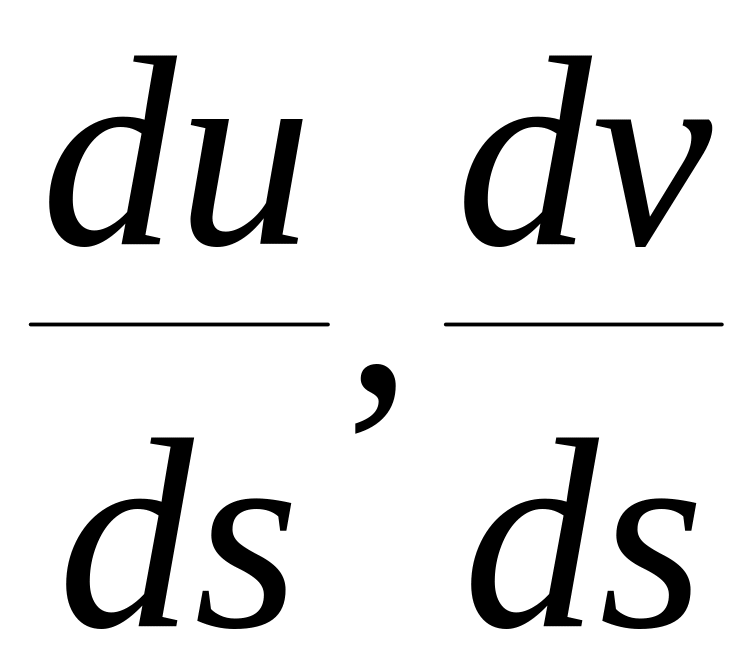или . Формула (2). показывает, что 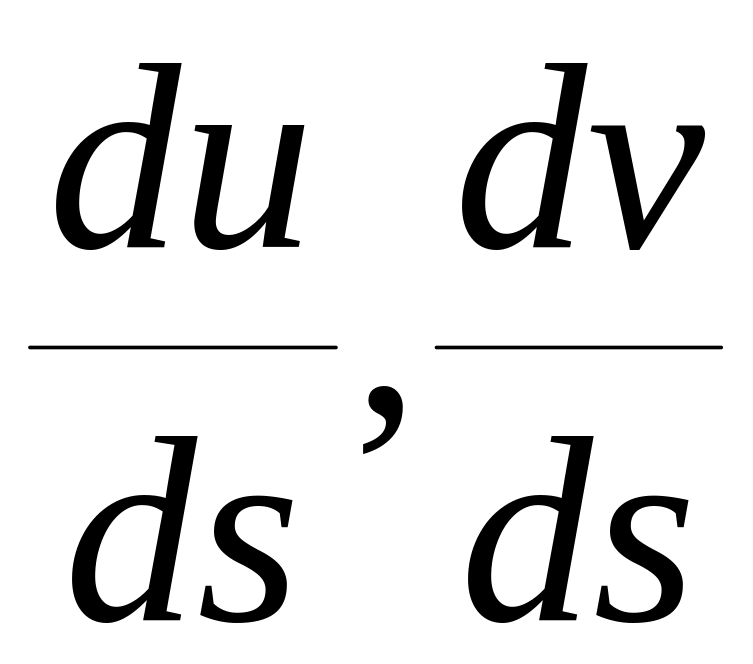- коорд-ты касательного вектора , но он один и тот же, сл-но, и кривизна у них одна и та же.

Сл. Пучок кривых, касающихся в точке М, имеют одну и ту же норм. кривизну в точке М. А просто кривизна у них разная, так как они изогнуты по-разному.

Среди этих кривых в этом пучке кривых выберем самую простую, так называемое нормальное сечение. Эта кривая получается сечением пов-ти пл-тью, проходящей через нормаль и общую касательную ко всем этим кривым. Эта кривая наз-ся плоской кривой, так как лежит в пл-ти.

Утв. Нормальная кривизна с точностью до знака есть кривизна норм. сечения.

Док-во. - касательный вектор, - нормальный вектор, направлен перпендик-но касательной. Из построения видно, что и лежат на одной прямой. смотрит туда же куда и .

. Длина останется той же, а знак зависит от того, куда смотрит вектор

Нормальная кривизна некоторой линии на пов-ти – кривизна соот-щего норм. сечения.