5. Задачи принятия решений

5.1. Принятие решений в условиях риска

5.1.1. Критерии максимизации среднеожидаемого выигрыша и минимизации среднеожидаемого риска

Принятие управленческих решений предполагает наличие выбора наиболее выгодного варианта поведения из нескольких имеющихся вариантов в условиях риска или неопределенности. Такие задачи могут быть описаны матричными играми особого типа, в которых игрок взаимодействует не с другим игроком, а с окружающей средой.

В процессе принятия решения игрок имеет информацию о нескольких возможных состояниях окружающей среды и либо располагает оценками вероятностей состояний, которые может принять окружающая среда в данный момент времени (то есть действует в условиях риска), либо не располагает и в этом случае сталкивается с проблемой неопределенности относительно этих состояний. Подобные игры называются играми с природой. Под природой понимается вся совокупность внешних обстоятельств, в которых игрок принимает решение. Игрок при этом называется лицом, принимающим решение.

Методы принятия решений в условиях риска разрабатываются и обосновываются в рамках так называемой теории статистических решений. При этом когда состояниям природы поставлены в соответствие вероятности, заданные экспертно либо вычисленные, решение обычно принимается на основе критерия максимизации среднеожидаемого.

Критерий максимизации среднеожидаемого выигрыша используется, если заданы вероятности наступления состояний природы: p₁, p₂, … , p_n. Тогда оптимальной будет та стратегия, для которой достигается значение

Критерий минимизации среднеожидаемого риска также используется при заданных вероятностях наступления состояний среды. В этом случае оптимальной будет стратегия, для которой достигается значение

Замечание. Оптимальные стратегии по критерию максимизации среднеожидаемого выигрыша и минимизации среднеожидаемого риска совпадают.

5.1.2. Дерево решений

На практике результат одного решения заставляет нас принимать следующее решение и т. д. Когда нужно принять несколько решений в условиях риска, когда каждое решение зависит от ис­хода предыдущего решения или исходов испытаний, то применяют схему, называемую деревом решений.

Дерево решений - это графическое изображение процесса приня­тия решений, в котором отражены альтернативные решения, альтер­нативные состояния среды, соответствующие вероятности и выиг­рыши для любых комбинаций альтернатив и состояний среды.

Рисуют деревья слева направо. Места, где принимаются решения, обозначают квадратами (□), места появления исходов – кругами (○), возможные решения - пунктирными линиями (----------), возможные исходы - сплошными линиями (________).

Для каждой альтернативы мы считаем ожидаемую стоимостную оценку (EМV) - максимальную из сумм оценок выигрышей, умно­женных на вероятность реализации выигрышей, для всех возможных вариантов (как в п. 5.1.1).

Пример. Главному инженеру компании надо решить, монти­ровать ли новую производственную линию, использующую но­вейшую технологию. Если новая линия будет работать безотказно, компания получит прибыль 200 млн. рублей. Если же она откажет, компания может потерять 150 млн. рублей. По оценкам главного ин­женера, существует 60% шансов, что новая производственная линия откажет. Можно создать экспериментальную установку, а затем уже решать, монтировать или нет производственную линию. Экспери­мент обойдется в 10 млн. рублей.

Главный инженер считает, что суще­ствует 50% шансов, что экспериментальная установка будет работать. Если экспериментальная установка будет работать, то 90% шансов за то, что смонтированная производственная линия также будет рабо­тать. Если же экспериментальная установка не будет работать, то только 20% шансов за то, что производственная линия заработает. Следует ли строить экспериментальную установку? Следует ли мон­тировать производственную линию? Какова ожидаемая стоимостная оценка наилучшего решения?

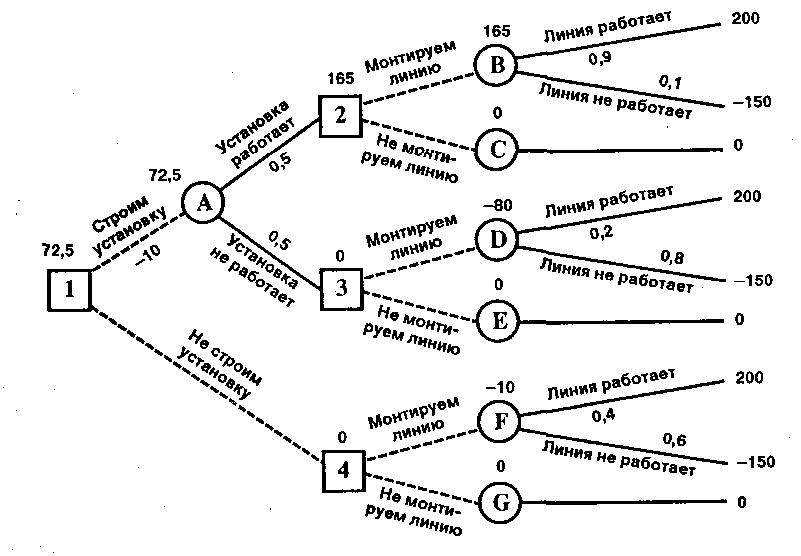
Рис.3. Дерево решения

В узле F возможны исходы «линия работает» с вероятностью 0,4 (что приносит прибыль 200 млн. рублей) и «линия не работает» с вероятностью 0,6 (что приносит убыток -150 млн. рублей). Следовательно, оценка узла F

млн. рублей.

Это число мы пишем над узлом F.

В узле 4 мы выбираем между решением «монтируем линию» (оценка этого решения ) и решением «не монтируем линию» (оценка этого решения ):

Эту оценку мы пи­шем над узлом 4, а решение «монтируем линию» отбрасываем и за­черкиваем.

Аналогично:

Поэтому в узле 2 отбрасываем возможное решение «не монтируем линию».

Поэтому в узле 3 отбрасываем возможное решение «монтируем линию».

Поэтому в узле 1 отбрасываем возможное решение «не строим установку».

Ожидаемая стоимостная оценка наилучшего решения равна 72,5 млн. рублей. Строим установку. Если установка работает, то монтируем линию. Если установка не работает, то линию монтировать не следует.

Задачи 41-50. Построить дерево решения и найти оптимальную стратегию поведения

Компания рассматривает вопрос о строительстве завода. Возможны три варианта действий:

а) построить большой завод стоимостью М₁ тысяч долларов. При этом варианте возможны большой спрос (годовой доход в размере R₁ тысяч долларов в течение следующих 5 лет) с вероятностью р₁ и низкий спрос (ежегодные убытки R₂ тысяч долларов) с вероятностью р₂;

б) построить маленький завод стоимостью М₂ тысяч долларов. При этом варианте возможны большой спрос (годовой доход в размере Т₁ тысяч долларов в течении следующих 5 лет) с вероятностью р₁ и низкий спрос (ежегодные убытки Т₂ тысяч долларов) с вероятностью р_2;

в) отложить строительство завода на один год для сбора дополнительной информации, которая может быть позитивной или негативной с вероятностью р₃ и р₄ соответственно. В случае позитивной информации можно построить заводы по указанным выше расценкам, а вероятности большого и низкого спроса меняются на р₅ и р₆ соответственно. Доходы на последующие четыре года остаются прежними. В случае негативной информации компания заводы строить не будет.

Какое решение следует принять руководству компании и на какие финансовые последствия при этом рассчитывать?

	М1	М2	р1	р2	р3	р4	р5	р6	R1	R2	Т1	Т2
41	600	350	0,7	0,3	0,8	0,2	0,9	0,1	250	50	150	25
42	605	345	0,65	0,35	0,75	0,25	0,91	0,09	245	45	145	20
43	610	340	0,75	0,25	0,85	0,15	0,92	0,08	240	40	140	15
44	615	335	0,7	0,3	0,85	0,15	0,93	0,07	235	3	135	10
45	620	330	0,65	0,35	0,8	0,2	0,94	0,06	230	30	130	5
46	625	325	0,75	0,25	0,75	0,25	0,95	0,05	255	55	155	30
47	630	320	0,7	0,3	0,75	0,25	0,94	0,06	260	60	160	35
48	635	315	0,65	0,35	0,85	0,15	0,93	0,07	265	65	165	40
49	640	310	0,75	0,25	0,8	0,2	0,92	0,08	270	70	170	45
50	645	305	0,7	0,3	0,75	0,25	0,91	0,09	275	75	175	50