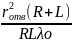7 Полосы равной толщины. Кольца Ньютона.

При интерференции света от пленки переменной толщины на пов-ти образ. Полосы называемые полосы равной толщины. Здесь толщина относ-ся не к ширине полосы , а к толщине клина на месте которой образ интерференц. Полоса.

Чтобы наблюд интерференц картину на пов-ти клина надо глаз аккомодировать на пов-ть клина. Частным случаем полос равной толщины будут кольца Ньютона. Интерференц картина в виде колец наблюд в приборе Ньютона. Ньютон взял плоско || пластинку , на эту пластинку положил плосковыпукл линзу, выпуклой стороной к пластинке. В результате чего между пластинкой и линзой образ воздушный зазор в виде сферического клина. Воздушн зазор как пленка выполн главн роль в интерференции.

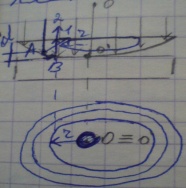
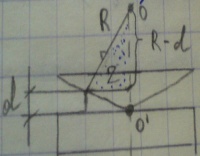
За счет отражения лучей от верхней и нижней граней воздушной пленки-зазора образ интерференц картина в виде колец радиуса r. Из рисунка вытекает:

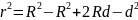
Здесь 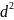- величина бесконечно малая, ею можно пренебречь 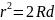(1)

Толщину зазора соответств данному радиусу кольца найдем оценив оптич разность хода лучей образовавшихся при отражении от верхней и нижней граней воздушного клина. Оптич разность хода:

К оптич разности хода добавляем т к 2-ой луч в т В отраж от оптически более плотной среды. Линза большого радиуса, угол клина очень мал, лучи падающие на клин практически перпендик. И угол падения можно принять =0 а=0. а=о sin0=0 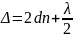если наблюд темное кольцо, то выполняется условие минимума : min отсюда получаем :

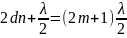
, где n-показатель преломления среды в зазоре. В данном случае n=1(вакуум).

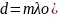подстав в формулу (1) 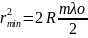радиус темного кольца: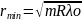

Радиус светлых полос: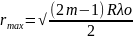 в отраженном свете в центре наблюд темное пятно - оптич разность хода. В центре d=0 следует , оптич разность хода= нечетному числу длин полуволн.

Замечание : интерференц картину в пленках можно наблюдать не только в отраженном свете но и проходящем. В этом случае оптич разность хода: 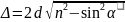оптич разность хода лучей в проходщем свете отличается от разности хода в отраженном свете на

В этом случае интерференц картина в проходящем свете будет противоп интерференц картине в отраж свете. для данной толщины d, если в отраж свете наблюд max, то в проходящем- min. Если наблюд кольца Ньютона в проходящем свете то интерференц картина будет против картине в отраж свете. Формулы радиусов колец поменяются местами

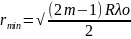
8Дифракция света. Принцип Гюйгенса-Френеля. Метод зон Френеля. Дифракция от круглого отверстия.

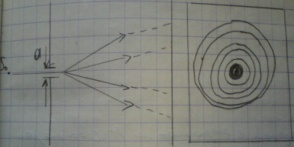
Свет распростр прямолинейно только в однородной среде не имеющей никаких преград на его пути. Так если на пути света поместим какую-либо преграду или диафрагму, то получаем резкую границу света и тени

Если возьмем отверстие, размер которого соизмерим с длиной волны, то на экране наблюдаем систему интерференц полос в виде колец. Этот опыт показ что свет проникает в область геометр тени и наблюдаются отклонения от законов геометр оптики

Дифракцией назыв сов-ть явлений наблюдаемых при распростран света в среде с резкими неоднородностями и связанных с отклонениями от законов геометр оптики. Дифракция приводит к огибанию световыми волнами препядствий и проникновению света в область геометр тени. для наблюдения дифракции необход соблюд след условия:

-размеры препядствий должны быть соизмеримы с длиной волны.

Чтобы объяснить дифракцию Френель воспользовался ренее известными положениями Гюйгенса , добавив добавив некотор свои утверждения, котор вошли в теорию дифракции как принцип Гюйгенса-Френеля.

1)каждая т волнов пов-ти явл самастоят когерентным источником. Вторичные источники эквивалентны одному и тому же источнику.

2)волновое возмущение в некотор т М можно рассматр как результат интерференции элементарн волн пришедших от кажд элемент участка волновой пов-ти

3)если на волнов пов-ти выделим равные по площади участки в результате имеющие одинаков кол-во вторичных источников, то мощности вторичного излучения равных по площади участков в волнов пов-ти равны.

4)преимуществ излучение от вторичн источников идет в направлении внешней нормали к волнов пов-ти

Амплитуда колебаний вызванных в т наложения вторичных волн (т М) будет тем меньше чем больше r-расстояние. Это оказыв влияние на интенсивность света в т М т.к I интенсивность пропорцион-на квадрату амплитуды. Пользуясь данн принципами Френель разбив волнов пов-ть на участки равные по площади названные зонами Френеля.

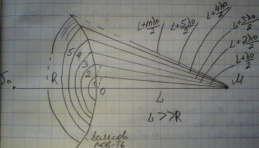
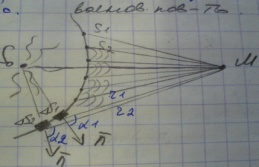
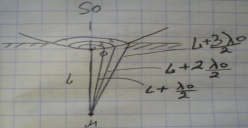
R-радиус волнов пов-ти; L-расст от центра волнов пов-ти до наблюдателя,м

Зоны Френеля это шаровые кольца построенные так, что расст от краев кажд зоны Френеля до т М отлич на 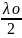границей центр зоны служат т волнов пов-ти находящейся не расст L+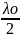 тогда границами след зон Френеля будут т наход на расст ; ; ….

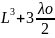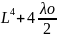- радиус m-ой зоны Френеля. Рассморт 2 прямоугольных треугольника можем получить соотношение для радиуса m-ой зоны Френеля

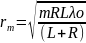, где m- номер зоны Френеля; R- радиус волнов пов-ти; L-расст от центра волнов пов-ти до наблюдателя. Зона френеля равна по площади разности 2-х сегментальных смежных пов-тей

данн соотношение не зависит от номера зоны в результате площади зон Френеля одинаковы. Зоны Френеля удалены от наблюдателя на расст r1<r2<r3<r4<…<r m, чем дальше зона от центра волнов пов-ти тем больше расстояние.т.к

r1= L+ ; r2= ; r3= амплитуды колебаний , вызванных волнами пришедшими от зон Френеля монотонно убывают А1>A2>A3>A4>…>Am волны от двух соседних зон приходят в противофазах (Δφ=π) т.к разность хода волн до т наложения равна

при наложении волн от двух соседних зон вызывает ослабление. Из амплитуд колебаний из зон Френеля: А=А1-А2+А3-А4+А5-А6+А7-… Аm

10 9 7 6 5 4 3 2 1

8=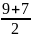 6= воспольз свойством монотонно убывающего ряда

Ак=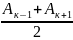 , т.е амплитуда любой к-ой зоны есть среднее арифметическое среди амплитуд послед и предыдущ зон Френеля. А=А1-А2+А3-А4+А5-А6+А7-… Аm амплитуды от нечетн зон разделим на 2 половинки

А=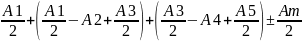

A= ,

Знак + - если m=нечетн число

- - если m=четн число зон Френеля

Вывод: в т М наблюд мах интенсивности когда в волнов пов-ти уклад нечетное число зон френеля, а мин интенсивности когда в волнов пов-ти уклад четное число зон Френеля

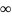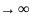Если на пути светов волны нет никаких преград т.е волнв пов-ть полностью открыта то число зон френеля т стремится к m , а Am 0 тогда результир амплитуда : А= = получаем что действие всей волнов пов-ти эквивалентно половине действия центр зоны. Размеры центр зоны очень малы получается, что свет от центр зоны идет в виде узкого прямолин канала т. Е практически прямолинейно.

Дифракция от круглого отверстия отверстие – диафрагма закрыла все зоны начиная с (к+1)

А=А1-А2+А3-А4…

A=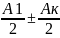 если число зон к- нечетное , то в т М наблюд мах, если к-четное , то мин . чтобы узнать сколько зон Френеля открыв диафрагмой примем что

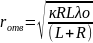
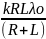= k=