18.2. Суммирование случайных погрешностей с распределениями, отличными от нормального

Для получения доверительного интервала суммарной погрешности, пользуются выражением δ_Σ = ±k_pσ_Σ, где коэффициент k_p определяется из формы закона распределения. Для нахождения закона распределения суммы погрешностей, и, отсюда, коэффициента k_p применяются методы теории вероятностей.

Возможны приближенные способы вычисления k_p без установления закона распределения суммарной погрешности.

Первый способ базируется на ЦПТ (центральной предельной теореме): если суммируется достаточно большое количество независимых случайных величин (n ≥ 5), то в качестве k_p можно брать Z_p.

Второй способ базируется на экспериментальном исследовании. Показано, что при суммировании независимых составляющих погрешности, имеющих симметричные законы распределения (равномерный, треугольный и т.п.) k_(0,9)  1,6; k_(0,95)  1,8.

Заметим, что границы доверительного интервала симметричны лишь при ∆_с = 0.

Пример. ∆_c = 0,1 В, δ_0,9 = ±0,3 В

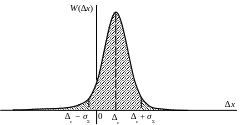
В этом случае, нам придется пользоваться интервалом [−0,2 ÷ 0,4] В, поскольку знак систематической погрешности неизвестен. Однако это усложнит дальнейшие расчеты. В этом случае искусственно вводят симметрию, выбирая границы интервала максимальными:

.

Поскольку выход за границы интервала значений погрешности наблюдается лишь с одной стороны, то вероятность выхода погрешности за границы доверительного интервала уменьшается в два раза. А, значит, при наличии систематической составляющей мы можем определить доверительный интервал на уровне 0,95 как

.

§19. Обработка результатов измерений

Цель любого измерения — установление значения измеряемой величины и оценка погрешности результата измерения. Погрешность ∆x является случайной величиной, следовательно, и x = x_изм ± ∆x является случайной величиной.

Мы знаем, что математическое ожидание закона распределения значения результата измерения смещено с истинного значения на величину систематической погрешности ∆_c, а дисперсия этого закона распределения равна дисперсии случайной погрешности. Тогда при обработке результатов нам потребуется оценить величину систематической погрешности и исключить ее из ряда наблюдений.

Отсюда следует, что при обработке результатов измерения необходимо произвести следующие шаги:

19.0. Выборочное распределение

Если имеется случайная величина x^*, принимающая значения с вероятностями по 1/n, то ее функция распределения равна

,

а само распределение называют выборочным или эмпирическим распределением.

Если положить, что x_i сами являются случайными величинами — результатами измерения величины x, то математическое ожидание x^*, дисперсия и прочие характеристики тоже станут случайными величинами. Ими широко пользуются для оценки (приближения) соответствующих неизвестных характеристик истинного распределения. При n → ∞ выборочные характеристики стремятся к истинным. На практике можно говорить о близости выборочного и истинного распределений при достаточно больших значениях n.

19.1. Оценка математического ожидания

Математическое ожидание x^* обозначают ; оно равно

.

часто называют средним (средним арифметическим) значением величины x.

При неограниченном увеличении числа измерений n . Поскольку n ограничено, то является случайной величиной, и можно говорить о ее математическом ожидании .

На практике величина принимается за действительное значение измеряемой величины, и тогда , а для дисперсии (при условии независимости результатов измерения) справедливо равенство

.