31.Задача об управлении ракетой как типовая задача теории оптимального управления.

Содержательные задачи ТУ проиллюстрируем примером движения ракеты в вертикально плоскости. Ракету рассматриваем как материальную точку. На нее действуют сила тяги двигателя, сила земного притяжения и т.д. Задача состоит в том, чтобы найти такую силу тяги двигателя, чтобы после старта перенести ракету в некоторую точку, а дальше отключить двигатель и она полетит как камень. На полет наложена система ограничений.После постановки задачи начинается ее формализация. 4 момента, формализующих всю содержательную постановку.

1. Построение мат.модели ракеты как объекта управления это система ОДУ, которая в данном случае выводится по второму закону Ньютона.

Ox:

Oy:

m – примерная масса ракеты, – проекции равнодействующих внешних сил(кроме силы тяги). Вспомогательные обозначения:

Система стандартного представления мат. модели ракеты:

2. Переход ракеты из А в В.

В каждом конкретном случае задачи управления.

3. Приходится считаться с рядом ограничений на управление и движение

а) – такое, чтобы не коснулось земли

б)если корабль с экипажем – надо считаться с радиационными поясами Земли.

в)

г) для любых t

д)

Задач ТУ, где нет ограничений на функцию управления не существует

4. Должно быть введено понятие качества управления. Оно предст. ф-налом,к-й задается на дв-ях и упр-ях.

Существует неединственное управление. Можно ставить задачу о выборе наилучшего.

В общем случае 4 момента: математическая модель, цель управления, ограничения на движение и управление,ф-нал хар-щий кач-во.

32. Постановка простейшей задачи поиска оптимального программного управления и её сведение к вариационной задаче на условный экстремум.

1. Будем считать, что задана система ОДУ:

; (1)

Компоненты функции F, по совокупности всех своих аргументов ( дважды непр дифф функция на [ )

Векторная функция (t) при конкретном – состояние объекта.

Векторная функция – характеризует программное управление.

Зададим фиксированные начальные и конечные положения ;

2. Цель управления – это перевод объекта из в : , где ,

3. Ограничения

4.

- дважды дифф на том же множестве

ОПРЕДЕЛЕНИЕ 1: Будем говорить, что кусочно-непрерывному на отрезке управлению соответствует движение объекта 1, если справедливо :

;

Замечание 1: t – всегда время

В соответствие с последней формулой нетрудно построить алгоритм построения движения, соответствующее данному уравнению

1. 

2. Подставим эту функцию в систему (1) :

3. Задаем вполне конкретное условие , где

4. Интегрируя (*) на отрезке получим . При кусочно-непрерывном будет кусочно-гладк.

Обратим внимание на то, что каждому управлению соответствует беск мн-во движений зависящие от

ОПРЕДЕЛЕНИЕ 2: Будем говорить, что управление переводит объект из начального положения в конечное положение за время если такое движение соответствует этому управлению для которой: , .

Вопрос о существовании управления, переводящего из начальной в конечную точку оставляем открытым. Будем считать, что оно , условия расскажут впоследствии.

Ведем в рассмотрение 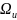– кусочно-непр вектор на отрезке – множество допустимых управлений.

ОПРЕДЕЛЕНИЕ 3: Управление будем называть оптимальным для объекта (1) по отношению к функционалу (2) если среди всех других управлений переводящим объект (1) из начального положения в конечное положение функционал достигает своего наименьшего значения , т.е.

,

Где }

- это движение объекта соответствует оптимальному управлению – оптимальное движение

В соответствии введенными определениями то простейшей задачей теории оптимального программного управления будем понимать задачу поиска оптимального управления соответствующее ему движение и минимальное значение функционала (2)

Как и раньше уделим внимание необходимым условиям экстремума в данной задаче, и рассмотрим ситуацию, которая позволит напрямую воспользоваться необходимыми условиями, которое мы получили для задач Лагранжа в вариационном исчислении.

В рамках данного параграфа

Т.о. рассмотрим только такие управления компоненты которых являются непр дифф функции на .

В этом случае рассматриваемая простейшая задача сводится к задаче Лагранжа и для этого сведения введем в рассмотрение составную вект функцию . Функционал (2) принимает вид Обратим внимание на то, что функционал (4) не зависит от производной (см частный случай параграф 2 глава 7 )

Введем в рассмотрение следующее множество функций

Введем в рассмотрение множество

С учетом введенных обозначений рассматриваемая простейшая задача эквивалентна поиску такой вект функции (предполагаем, что оно не пусто), кот обеспечивает min функционала (4). Такая задача есть задача Лагранжа из вариационного исчисления.

Однако из этой задачи есть 3 существенные особенности:

1. Min – ный функционал (4) не содержит производных от некоторых функций в подынтегральном выражении.

2. Краевые условия фиксированы для вектора только по 1-м компонентам, т.е. рассматриваемая задача является задачей с незакрепленными границами.

3. Особенность в сист дифф – ных связей определяющих множество содержит только n уравнении, что меньше чем n+m количества неизвестных функций. Причем по последним m функциям (компоненты уравнения ) связи являются голономными.