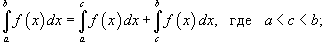27. Свойства определенного интеграла
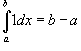
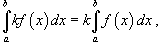где
k - константа;
Если
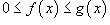для
всех
,
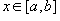то
.
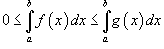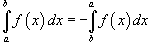
Если
в
интервале [a, b], то
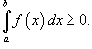
28. Формула Ньютона- Лейбница.
Пусть функция f (x) непрерывна на замкнутом интервале [a, b]. Если F (x) - первообразная функции f (x) на [a, b], то
Формула Ньютона - Лейбница дает правило вычисления определенного интеграла: значение определенного интеграла на отрезке [a;b] от непрерывной функции f(x) равно разности значений любой ее первообразной , вычисленной при x=b и x=а.
29)Замена переменной и формула интегрирования по частям для определенного интеграла.
Замена переменной.
Пусть
функция
:
1)определена,
непрерывно дифференцируема и монотонна
на отрезке
2)
3)функция
непрерывна на отрезке (а,в)
Тогда
:
.
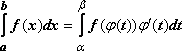Док-во:
пусть F(x)-первообразная
для функции f(x),т.е.
f(x)= F`(x),
тогда
-
первообразная для функции
.
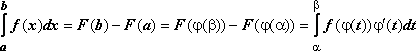,что
и требовалось док-ть.
Формула интегрирования по частям для определенного интеграла.
Если
u(x),v(x)-дифференцируемые
функции, то
.
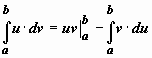Док-во:
интегрируем равенство
,в
пределах от а до в:
.
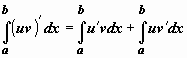Функция
в левом интеграле имеет первообразную
uv, по формуле
Ньютона-Лейбница
,
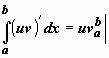следовательно,
,
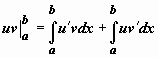откуда и следует доказываемое равенство.
Пример:
.
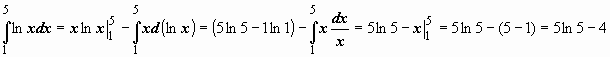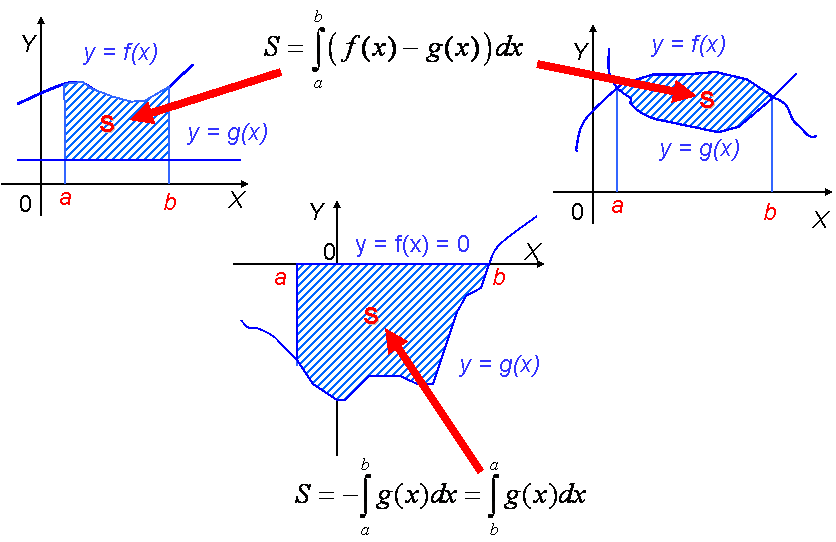
30 Вычисление площадей плоских фигур
Рассмотрим плоскую фигуру, представляющую собой множество точек плоскости лежащих в полосе между прямыми x = a, x = b и ограниченное сверху графиком непрерывной функции y = f(x) и снизу графиком непрерывной функции y = g(x) . Причем f(x) > g(x) на промежутке (a; b) и f(a) = g(a), f(b) = g(b).
Примеры плоских фигур
32.Теория вероятности. Случайные события.
Теория вероятностей изучает закономерности, возникающие в случайных экспериментах. Случайным называют эксперимент, результат которого нельзя предсказать заранее. Невозможность предсказать результат отличает случайное явление от детерминированного.
|
Два события называются равновероятными (или равновозможными), если нет никаких объективных причин считать, что одно из них может наступить чаще, чем другое.
Вероятностью P(A) события в данном опыте называется отношение числа M исходов опыта, благоприятствующих событию A, к общему числу N возможных исходов опыта, образующих полную группу равновероятных попарно несовместных событий:
