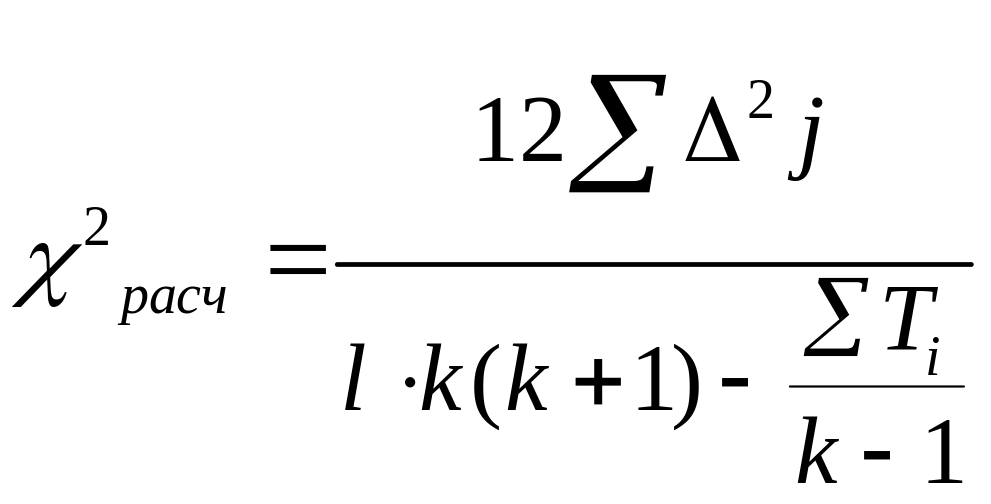25. Способы отсеивания факторов с помощью полностью насыщенных планов.

При отсеивающем эксперименте стараются сократить число опытов, накладывая некоторое ограничение в процессе самой постановки задачи.

Предполагают, что наиболее сильно на ПО влияют только линейные эффекты, т.е. Факторы сами по себе. Взаимодействия факторов влияет слабее. Тогда можно применить полностью насыщенные планы, где число опытов равно числу оцениваемых коэффициентов регрессии, включая свободный член. Такие планы можно построить или в виде дробной реплики, или с помощью специальных ортогональных планов — Планов Плакетта Бормана. Они содержат число опытов n, кратное 4. Для их составления существует специальная таблица.

Так же используется метод перевала. Он позволяет отделить линейные эффекты от парных эффектов взаимодействия. Опыты полностью насыщенного плана выполняют дважды. Во второй серии меняют все знаки матрицы планирования на обратные. Если затем эти 2 эксперимента рассмотреть вместе, то можно оценить линейные эффекты отдельно от парных взаимодействий, следовательно можно проверить гипотезу о линейности модели.

26. Основная идея, положенная в основу всех методов отсеивания факторов.

Все способы основаны на том, чтобы можно было все факторы ранжировать.

При отсеивающем эксперименте стараются сократить число опытов, накладывая некоторое ограничение в процессе самой постановки задачи.

Предполагают, что наиболее сильно на ПО влияют только линейные эффекты, т.е. Факторы сами по себе. Взаимодействия факторов влияет слабее. Поэтому стараются выявит линейные эффекты, чтоб они не затеняли малозначимые.

27. Метод априорного ранжирования факторов и последовательность его выполнения.

Необходимо составить представление о том явлении, которое мы будем изучать.

Проводится опрос специалистов, и составляем диаграмму рангов.

Предполагается заполнить анкету включая список всех факторов, способ их определения, размерность, предполагаемые интервалы варьирования.

При помощи анкет опросили специалистов 2-ч научных школ, которых попросили проранжировать влияние групп легирующих элементов на жаропрочность. По результатам опроса составили таблицу.

Затем необходимо проверить, на данном примере, как внутри школ так и вместе, насколько согласованны между собой специалисты. Делается это при помощи коэффициента конкордации (Кендела):

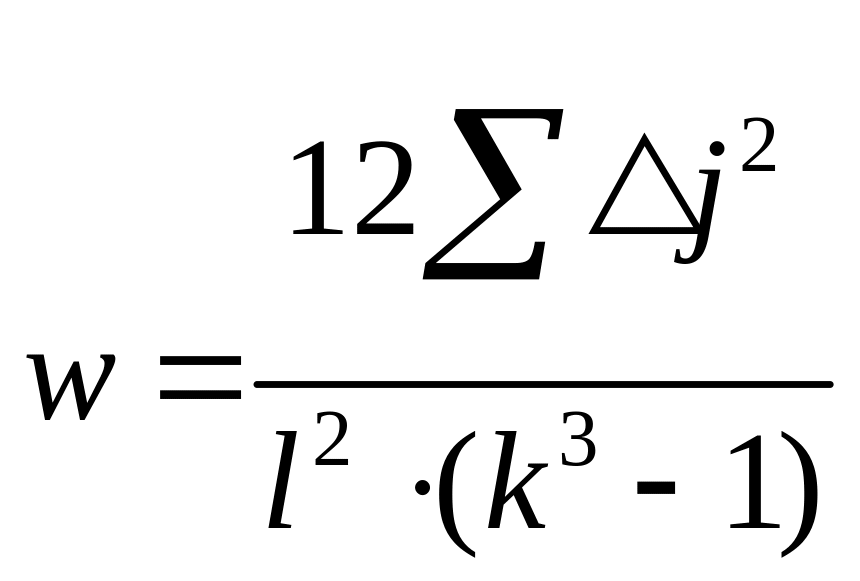, где L-число исследователей, К-кол-во факторов.

Если w=0, это означает отсутствие какого-либо согласия во мнениях исследователе, если w=1, полное согласие по влиянию факторов. Существенность коэф. w устанавливают при помощи критерия Пирсона.

Критерий Пирсона- это критерия согласия или критерий проверки гипотезы о предполагаемом законе неизвестного распределения.

Критерий не доказывает справедливость гипотезы, а только устанавливает на принятом уровне значимости её согласованность или несогласованность с данными наблюдений.

По таблице находим кр. Пирсона и сравниваем с расчетным.

Гипотеза о наличии согласия между исследователями принимается в том случае, когда

Далее строим априорные диаграммы рангов, чтобы определить степень влияния каждого из факторов на параметр оптимизации:

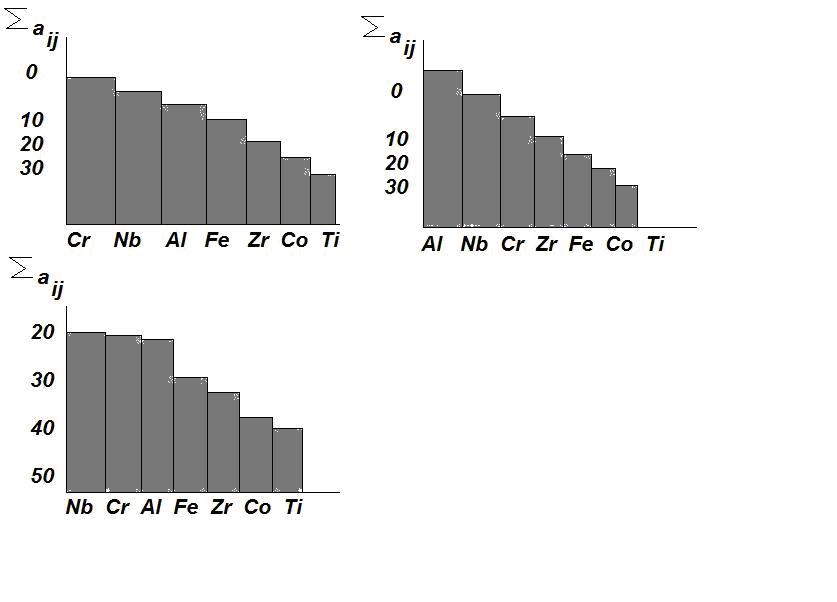
Слева на право, ранжированные шкалы исслед. 1, ранжированные шкалы исслед. 2, общая ранжировка.

Если распределение факторов по рангам не равномерно, убывание монотонное, хотя различия и делаются, но неуверенно, след, в эксперимент надо вкл. все факторы. Если не равномерно, убывание быстрое, близкое к экспоненциальному, след, выбирают ряд наиболее сильно влияющих факторов. Если распределение равномерное, след., исследователи не могут выбрать наиболее влияющие факторы ( факторы мало влияют либо мало информации)

Иногда исследователь не может четко разграничить 2 и более членов в ряду, след., вводят связанные ранги.

В этом случае коэф. конкордации : 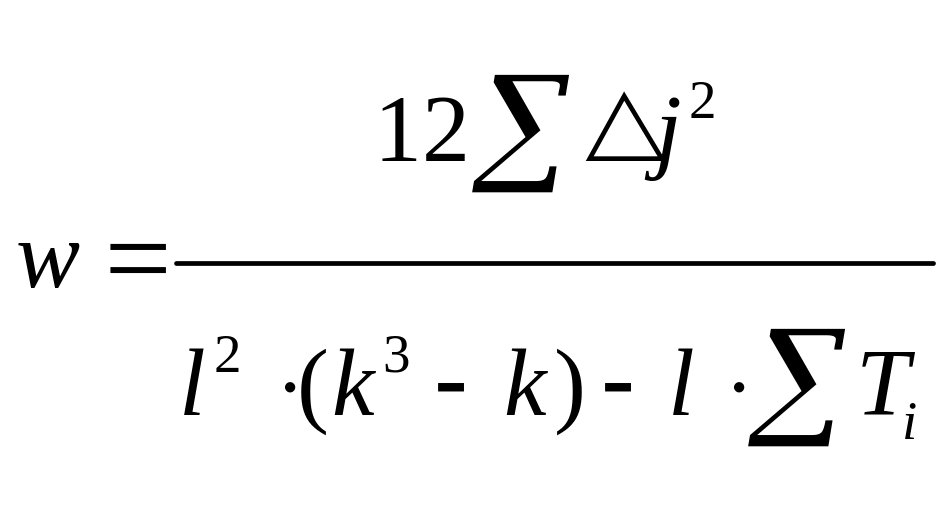, где , - число одинаковых рангов в i-ом ранжировании, L- число исследователей.

При наличии связанного ранга, критерий Пирсона: