9. Метод перебора при решении компромиссных задач

Рассматриваем различные варианты и выбираем наиболее удовлетворительные и экспериментально проверяем. В нашей задаче зависит ли жаропрочность от др. факторов. Далее по уравнениям зависимости пластичности, свариваемости и коррозионной стойкости определяют соответствующие свойства.

10.Получение приближенных оценок коэффициентов регрессии по выделенным эффектам.

Выделившиеся точки – точки, которые принадлежат какому-либо уровню фактора и находится выше самой верхней или ниже самой нижней. Чем больше разность между медианой и числом выделившихся точек, тем сильнее влияет фактор. Факторы можно выделить либо по разности медиан, либо по числу выделенных точек. Но лучше определить по произведению ǀ = .

Затем строят таблицу с n входами для оценки эффектов. Число входов не ограничено. В каждой клетке определяют . количественной оценкой является разность между средними величинами и среднем по клеткам.

–

Далее проверяют статистическую значимость эффектов по критерию Стьюдента

- эффект, - среднеквадратическая ошибка , характеризующая отклонение среднего эффекта относительно среднего значения величины, – число наблюдений в i-ой клетке.

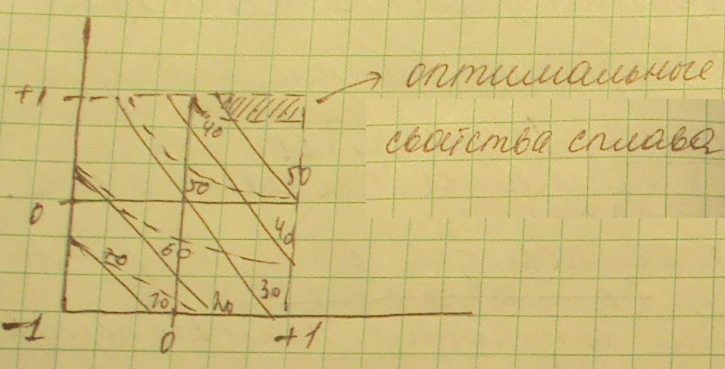
11.Графический способ поиска компромисса.

Основан на том, что рассматривают совмещенные двухмерные сечения поверхностей отклика и визуально определяют подходящие условные экстремумы.

Пример. В задаче изучалось влияние 2х элементов х1 и х2 на предел прочности у1 и ломкости у2. Нужно получить сплав с пределом прочности 50 кг/ и горячеломкостью 40%.

После планирования 2го порядка были получены уравнения связи у1 и у2:

у1 = 29,6+10·х1+11,5·х2+1,5·х1·х2+6· +6,5· (1)

у2 = 44-6·х1-18·х2-6·х1·х2+15· +6· (2)

Из простого анализа коэффициентов уравнений нельзя сказать, в какую сторону надо менять параметры оптимизации. Чтобы у1 увеличился, нужно чтобы х1 увеличился. В тоже время , у2 может уменьшиться, а может вырасти. Поэтому (1) и (2) представляют графически в виде двухмерных сечений.

12.Критерий, по которому заканчивают отсеивание факторов и их взаимодействий.

- (когда ) условие окончания отсеивания значимых факторов (ошибка предсказания меньше ошибки опыта). Если . следовательно рассеяние относительно среднего значения велико и и нельзя выделить все сильно влияющие факторы.

13.Шкала желательности и правила пользования ею.

Желательность (d) – тот или иной желательный уровень свойства.

Существует шкала желательности. d может меняться от 0 до 1.

1.если d=1 , то это максимально возможный уровень качества.

2.d ϵ [0,8 ; 1) допустимый и превосходный уровень качества.

3. d ϵ [0,6 ; 0,8) допустимый и хороший уровень качества.

4. d ϵ (0,37 ; 0,6) допустимый и достаточный уровень качества.

5.d = 0,37 технический уровень качества, который соответствует тому значению свойства, который нужно получить.

6. d ϵ (0 ; 0,37) недопустимый уровень качества.

7.d = 0 максимально нежелательный уровень качества.

Функция желательности выражается уравнением d = и графически это уравнение выглядит так:

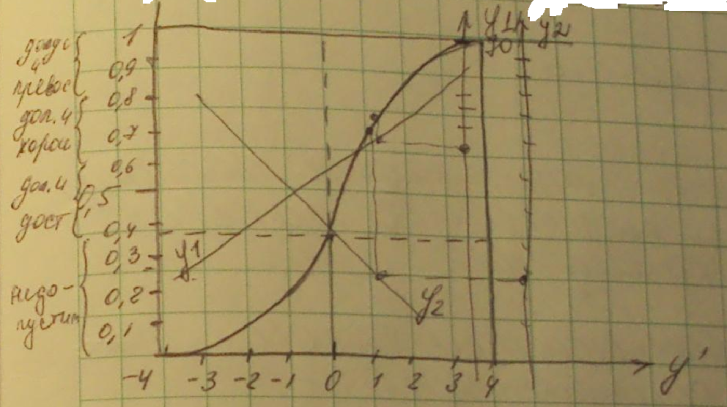
Для пользования функцией и шкалой желательности измеренное значение свойства переводят в безразмерное значение . затем устанавливают для каждого соответствующие желательности .