43. Вычисление площади плоской фигуры.

Вычисление площадей плоских фигур. Рассмотрим несколько случаев вычисления площадей плоских фигур.

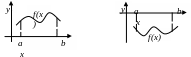
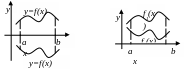
П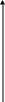 ример. Сделать чертеж и вычислить площадь фигуры ограниченной данными линиями , .

			8
			6
			4
			2
- 6	-4	-2	0	2	4	6
			-2

кв. ед.

44. Вычисление объема тела вращения.

Объем тела, образованного вращением вокруг оси криволинейной трапеции, ограниченной непрерывной кривой , осью абсцисс и двумя прямыми и , находится по формуле .

Пример. Найти объем тела, получающегося при вращении кривой вокруг оси от до . 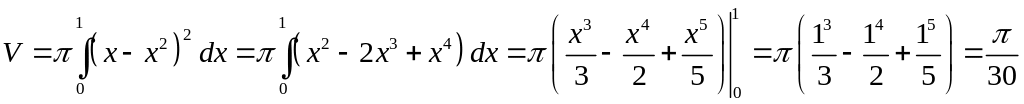куб. ед.

45. Вычисление длины дугиплоской кривой.

Если кривая на отрезке является гладкой (т.е. производная - непрерывная функция), то длина дуги этой кривой, заключенной между точками с абсциссами и , находится по формуле .

Пример. Найти длину дуги кривой от до .

Так как , то . Пусть , , , , тогда .

Пример. Найти длину дуги кривой между точками и в первой четверти.

Длину дуги кривой определим по формуле .Т. к. , , то .

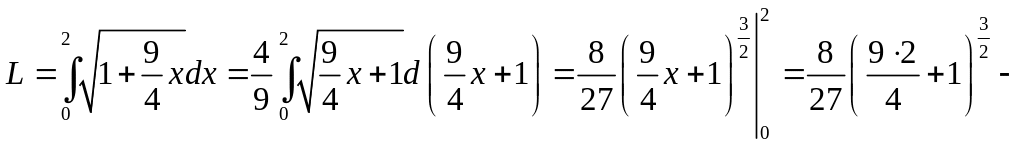
46. Вычисление площади поверхности тела вращения.

Площадь поверхности, образованной вращением оси дуги гладкой кривой между точками и , находится по формуле .

Пример. Найти площадь поверхности вращения вокруг оси дуги кубической параболы при .

Так как , то . Пусть , , , , тогда .

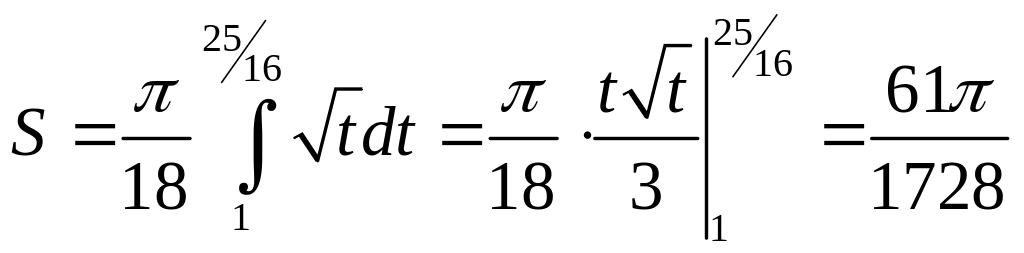57. Векторное пространство. Линейная зависимость векторов.

Определение. Вектор называется линейной комбинацией векторов векторного пространства , если он равен сумме произведений этих векторов на произвольные действительные числа: , где - какие угодно действительные числа.

Определение. Векторы векторного пространства называются линейно зависимыми, если существуют такие числа , не равные одновременно нулю, что .

В противном случае векторы называются линейно независимыми.

Определение. Линейное пространство называется -мерным, если в нем существуют линейно независимых векторов, а любые из векторов уже являются зависимыми.

Пример. Выяснить, являются ли векторы , , линейно зависимыми.

Составим векторное равенство . Записывая , , в виде вектор - столбцов, получим

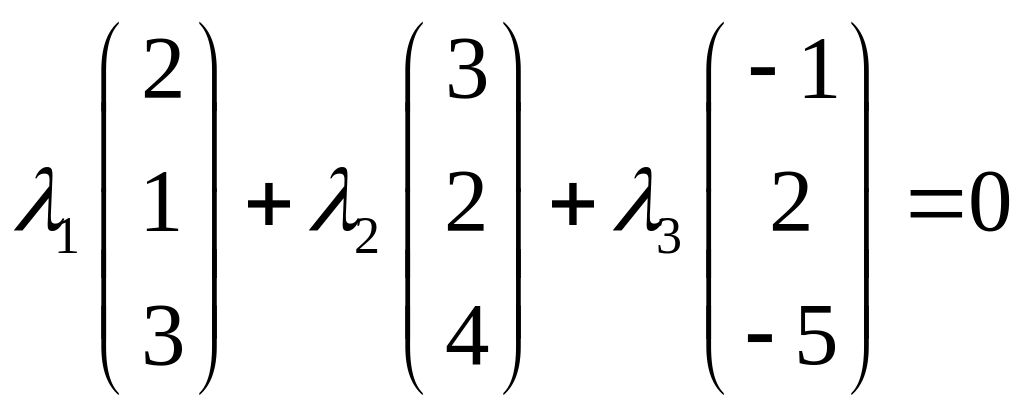
Задача свелась к решению системы: 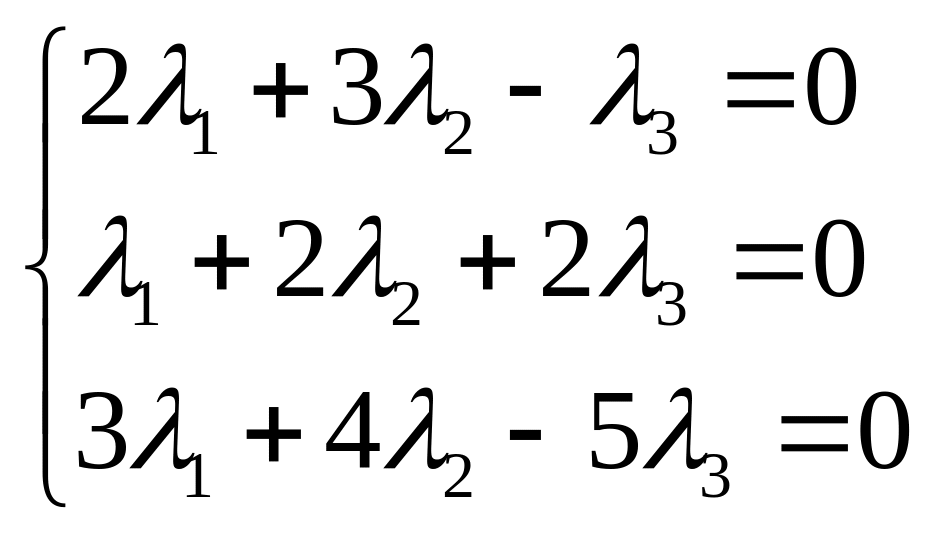. Решим систему методом Гаусса: 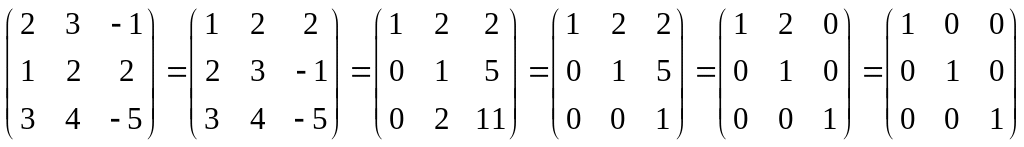. Следовательно, . Так как , то , , линейно независимы, следовательно, образуют базис.