32. Интегрирование функции .

Рассмотрим интегралы вида . Такие интегралы могут быть сведены к интегралам от рациональных функций заменой переменной , где . Действительно , , , .

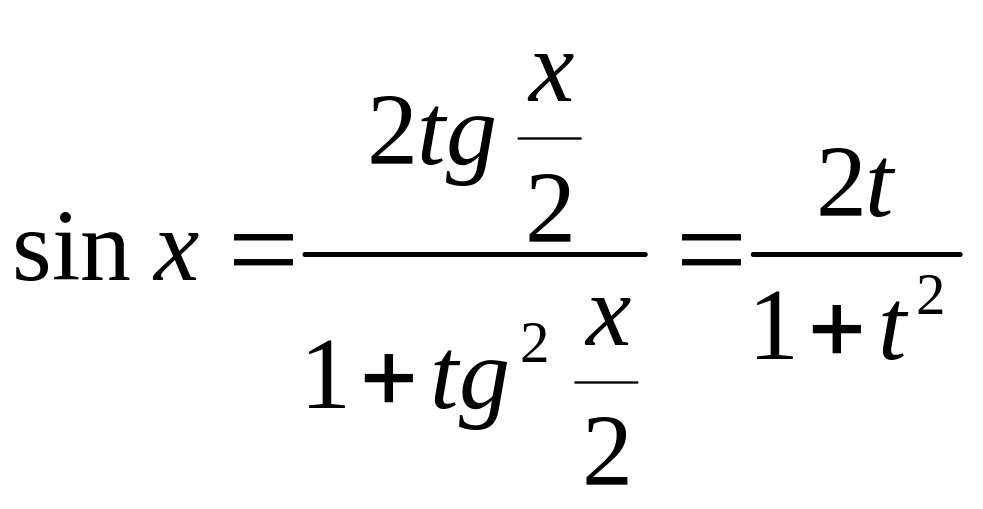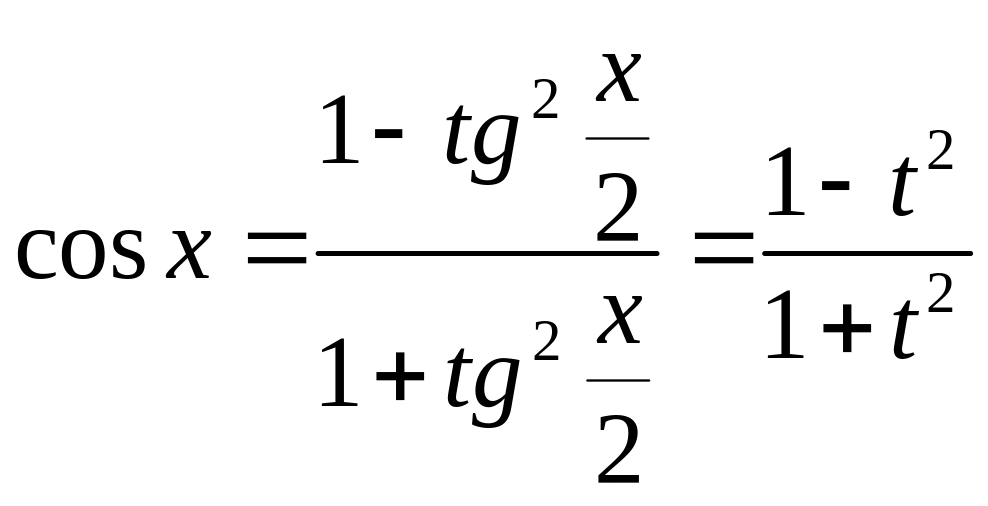Пример. Вычислить .

.

33 . Интегрирование функции , (первая подстановка Эйлера).

Интеграл вида , где рационализируется с помощью первой подстановки Эйлера .

Пример. Найти интеграл .

Здесь , поэтому применим подстановку . Возведем обе части равенства в квадрат , , приведем подобные члены, получим , откуда , .

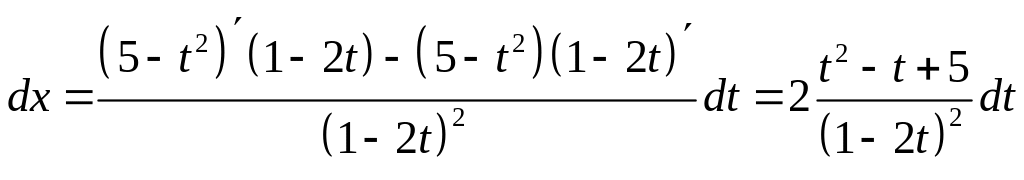Подставляя полученные выражения в данный интеграл, имеем

34 . Интегрирование функции , (вторая подстановка Эйлера).

Интеграл вида , где рационализируется с помощью первой подстановки Эйлера .

Пример. Найти интеграл .

Здесь , поэтому применим подстановку . Возведем обе части равенства в квадрат , , приведем подобные члены, получим , откуда , , .

Подставляя полученные выражения в данный интеграл, имеем Разложим подынтегральную функцию на сумму простейших дробей: , откуда Полагая , находим , при , получим , при имеем , тогда .

Таким образом, получаем

35 . Интегрирование функции , (третья подст.Эйлера).

Интеграл вида , где рационализируется с помощью первой подстановки Эйлера .

Пример. Вычислить .

Здесь , поэтому применим подстановку . Возведем обе части равенства в квадрат , , откуда , , .

Подставляя полученные выражения в интеграл, .

36. Определенный интеграл и его геометрический смысл.

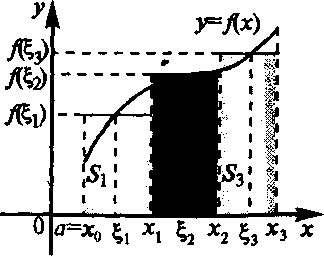Пусть функция неотрицательна на . Отдельное слагаемое интегральной суммы в этом случае равно площади прямоугольника со сторонами и , Другими словами, - это площадь под прямой на отрезке . Поэтому вся интегральная сумма равна площади под ломаной, образованной на каждом из отрезков прямой , параллельной оси абсцисс.

Определение. Пусть предел интегральной суммы при стремлении к нулю существует, конечен и не зависит от способа выбора точек , , … и точек , , ... Тогда этот предел называется определенным интегралом от функции на , обозначается , а сама функция называется интегрируемой на отрезке , т.е. .

Геометрический смысл определенного интеграла. Определенный интеграл численно равен площади криволинейной трапеции.

37. Основные свойства определенного интеграла.

1. Постоянный множитель можно выносить за знак интеграла, т.е. .

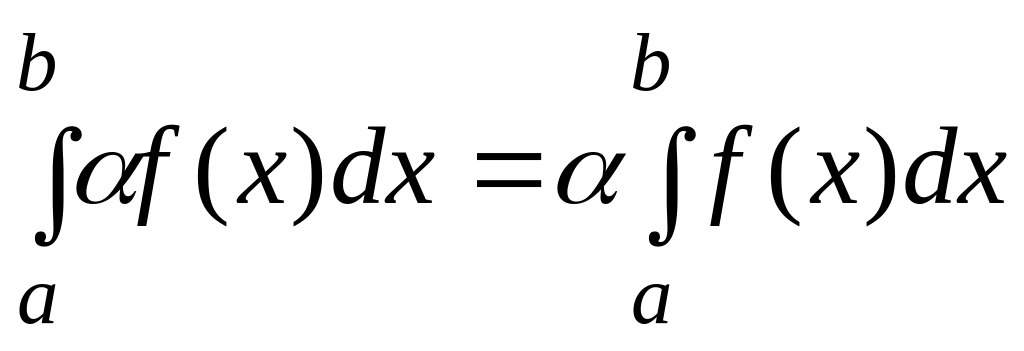2. Интеграл от алгебраической суммы двух функций равен такой же сумме интегралов от этих функций, т.е. .

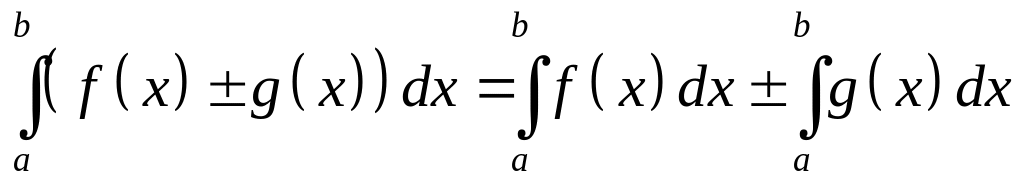3. Если отрезок интегрирования разбит на части, то интеграл на всем отрезке равен сумме интегралов для каждой из возникших частей, т.е. .

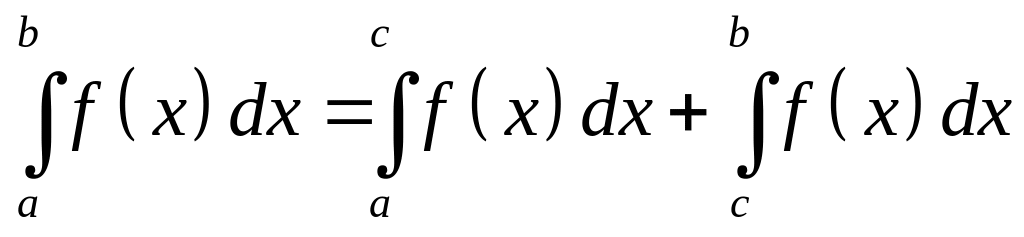38. Основные условия интегрируемости функций.

Теорема. Если функция непрерывна на отрезке , то она интегрируема на этом отрезке.

Пример. Вычислить .

Запишем выражение для интегральной суммы, предполагая, что все отрезки разбиения имеют одинаковую длину , равную , где - число отрезков разбиения, причем для каждого отрезка разбиения точка совпадает с правым концом этого отрезка, т.е. , где . В силу интегрируемости функции , выбор такого «специального» способа разбиения отрезка интегрирования на части и точек на отрезке разбиения не повлияет на искомый предел интегральной суммы. Тогда .

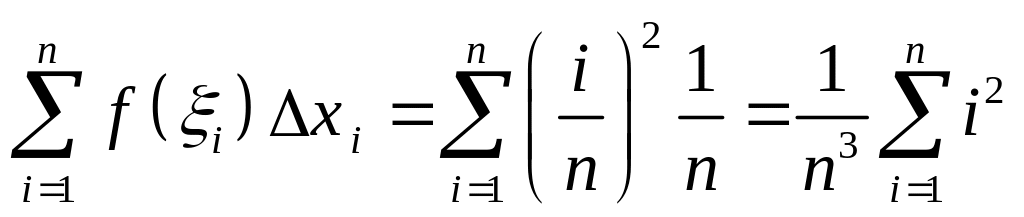Известно, что сумма квадратов чисел натурального ряда равна . Следовательно, .