Министерство образования и науки РФ Московский Государственный Открытый Университет Факультет информатики и радиоэлектроники Кафедра вычислительной техники и программирования
Курсовая работа По дисциплине: «Методы моделирования автономных систем» Тема: «Создание немодальной диалоговой панели для задания параметров, для запуска/останова вычислительного потока (нити), для контроля над ходом выполнения вычислений.»
Выполнил: студент 4 курса спец. 230105 Окулич-Казарин В.Е. шифр 608215
Проверил: Степанов М.В.
Москва 2012 г. |
Московский Государственный Открытый Университет
Факультет КИТ Кафедра ВТиП
Специальность (230105) ПОВТ
Задание
На курсовую работу Окуличу-Казарину В.Е.
(Ф.И.О.)
шифр 608215
1.Тема работы Создание немодальной диалоговой панели для задания параметров, для запуска/останова вычислительного потока (нити), для контроля над ходом выполнения вычислений
2.Исходные данные: Язык программирования Си, Microsoft Visual Studio
3.Содержание пояснительной записки
Численное решение итерационным методом
2D уравнения теплопроводности, Описание программы, Фрагменты исходного кода
4.Перечень графического материала
Снимок экрана с диалоговой панелью
5.Дата выдачи задания
6.Срок сдачи работы
Задание выдал Степанов М.В. ______________
(подпись)
Задание принял Окулич-Казарин В.Е. ______________
(подпись)
СОДЕРЖАНИЕ
1. |
Численное решение итерационным методом 2D уравнения теплопроводности |
4 |
2. |
Описание программы (Сведения о логической структуре и функционировании программы) |
6 |
2.1 |
Диалоговая панель «2D Управление теполопроводностью» |
6 |
2.2. |
Описание (назначение) функций |
10 |
2.3. |
Фрагменты исходного кода |
11 |
1. Численное решение итерационным методом
2D уравнения теплопроводности
Уравнение теплопроводности – нестационарное (изменяющееся со временем) дифференциальное уравнение в частных производных, для 2D случая имеет следующий вид:
,
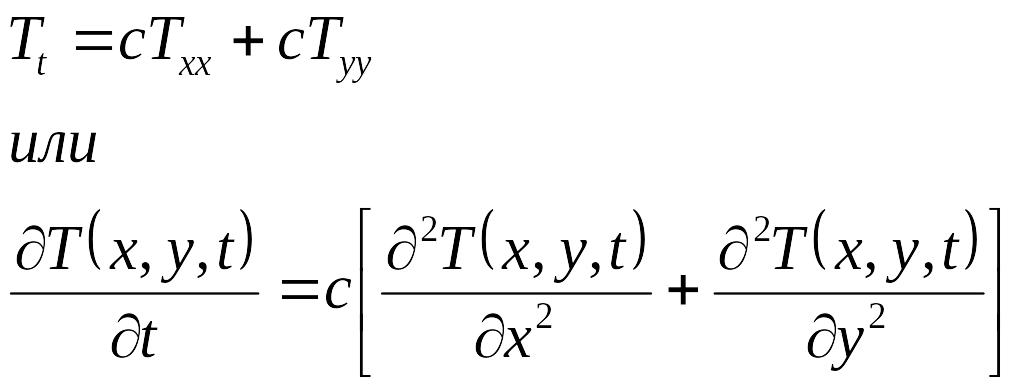(1)
где
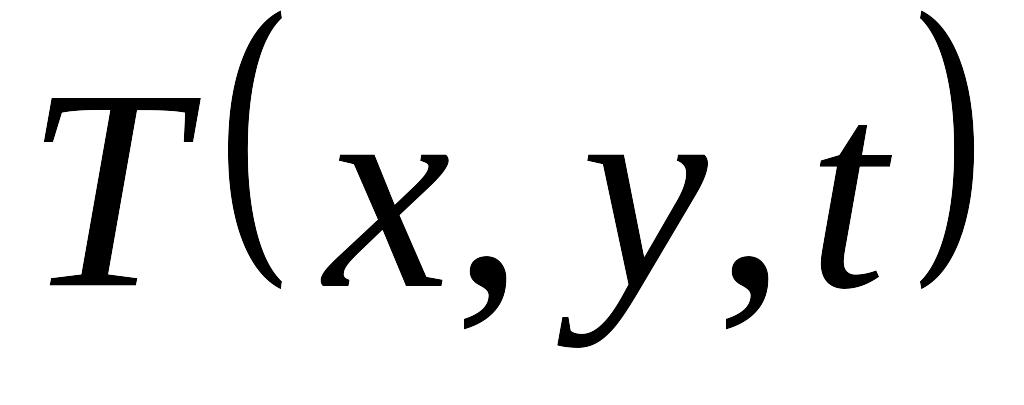– нестационарное
2D
распределение температуры,
– коэффициент
теплопроводности материала.
Введём
в функциональном 3D
пространстве
сетку с шагами
.
Для удобства вычислений – равномерную
по пространственным переменным
:
.
В основе простейшего итерационного
конечно-разностного метода решения
дифференциальных уравнений в частных
производных лежит замена:
в правой части (1) вторых производных центральными разностями по
;
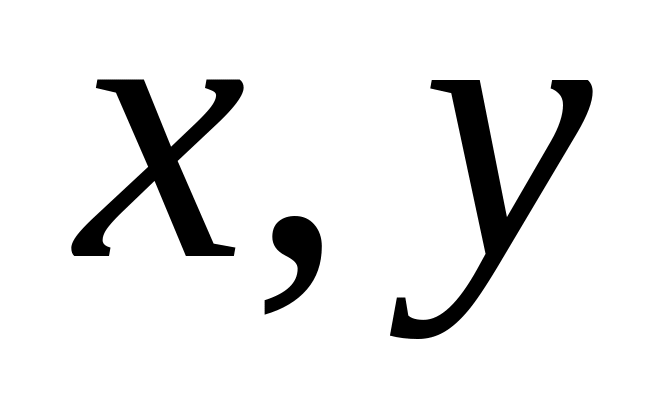в левой части (1) первой производной разностью вперёд по
.
.
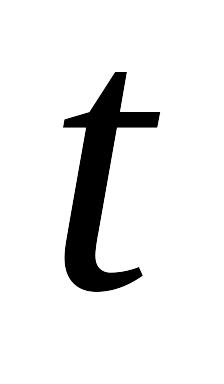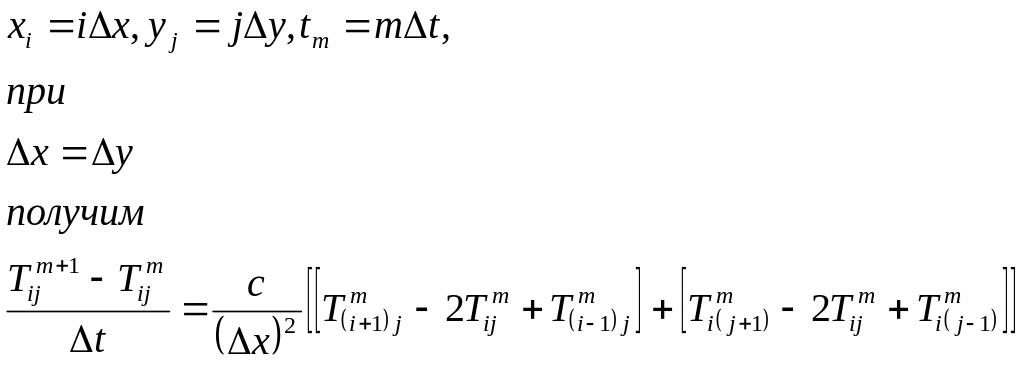(2)
Конечно-разностное уравнение (2) преобразуем в форму, удобную для итерационного решения:
.
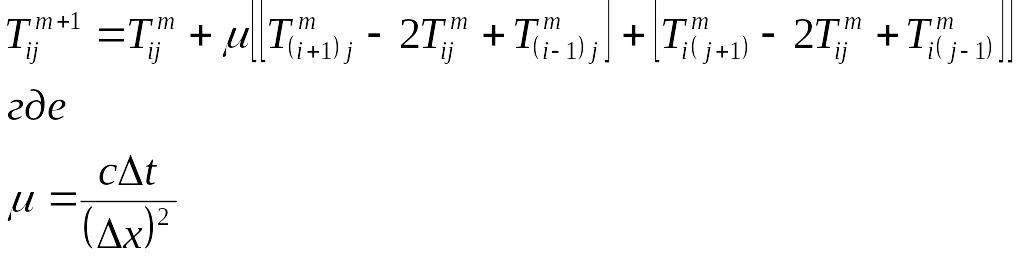(3)
Форма
(3) записи уравнения теплопроводности
(1) и (2) позволяет находить следующее по
времени
значение
исходя из известных на данный момент
текущих значений
.
Для итерационного процесса необходимо
задать начальные и граничные условия.
Начальные
условия определяют начальное 2D
распределение значений
при
.
Например, в начальный момент времени
точка с координатами
разогрета некоторым внешним воздействием
(удар микрометеорита по корпусу КА,
точечная подсветка мощным импульсом
лазерного излучения, монтажник точечно
задел горячим паяльником и т.п.) до
некоторой температуры:
.
(4)
Граничные условия определяют ситуацию на границах 2D диапазона вычислений
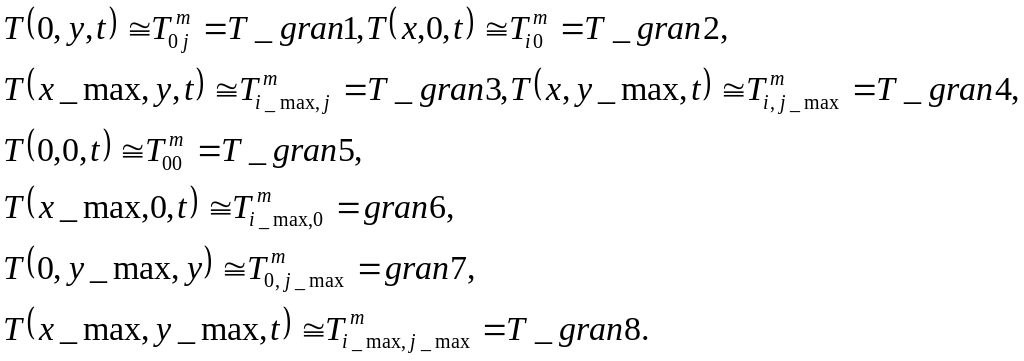(5)
Пусть внешнее воздействие в заданной точке привело к разогреву до температуры:
,
а температура на границах диапазона вычислений равна температуре окружающей среды, для простоты – комнатной температуре:
.
Имея
форму итерационной записи (3), начальные
(4) и граничные условия (5), можно найти
решение уравнения (1), то есть, рассчитать
динамику изменения 2D
распределения температуры
для последовательных моментов времени
.
Значение коэффициента
теплопроводности
является табличной величиной и
берётся из физических справочников.
Имеет размерность
.
Вообще-то, коэффициент теплопроводности
является функцией температуры:
,
но для упрощения расчётов примем, что
коэффициент теплопроводности является
константой и будем использовать табличные
значения при T=300K:
.
№ |
Материал (T=300K) |
Теплопроводность, Вт/см·К |
1. |
SiO2 (аморфный) |
0,014 |
2. |
Ge |
0,6 |
3. |
Si |
1,5 |
4. |
GaAs |
0,46 |
Описание программы (Сведения о логической структуре и функционировании программы)
Логическая структура и функционирование приложения основано на стандартной модели приложений для ОС с вытесняющей многозадачностью. Приложение разработано на языке C (Си) с помощью технологии процедурного программирования в стиле K&R C. Используется стандартный каркас приложения под ОС Microsoft Windows XP/Vista/7. Главная функция WinMain(…); запускает цикл обработки сообщений главного окна, который обрабатывает опции меню главного окна.
Результаты вычислений обрабатываются и визуализируются в дочерних окнах. Для 1D и 2D визуализации используются функции GDI API (Graphic Device Interface Applied Programming Interface), которые реализуют графические примитивы.