3.7 Нечіткі множини з нечіткими функціями належності

Причиною розгляду нечітких множин з нечіткими функціями належності є близький зв’язок, який існує між поняттям лінгвістичної істинності з такими значеннями, як істинно, цілком істинно, дуже істинно, більш-менш істинно і так далі, з одного боку, та нечіткими множинами, ступінь належності яким описується такими лінгвістичними термінами, як низький, середній, високий, дуже низький, не низький і не високий і т.д. — з другого.

Отже, припустимо, що А — нечітка підмножина універсальної множини U, а значеннями функції належності можуть бути нечіткі підмножини проміжку . Щоб відрізнити такі нечіткі підмножини множини від нечітких підмножин, розглянутих раніше, називатимемо їх нечіткими множинами типу 2, а нечіткі множини, функції належності яких є відображеннями — нечіткими множинами типу 1. Введемо більш загальне

Означення 3.1 Нечітка множина є множиною типу п, п=2, 3, ..., якщо значеннями її функції належності є нечіткі множини типу п-1. Функція належності нечіткої множини типу 1 приймає значення з проміжку .

Щоб визначити такі операції, як доповнення, об’єднання, переріз і т.д. для нечітких множин типу 2, природно використати принцип узагальнення. Для зручності виконаємо це в два етапи: спочатку узагальнимо відповідні означення для множин типу 1 на нечіткі множини з функціями належності, значеннями яких є проміжки, а потім, використовуючи принцип узагальнення в формі множин рівня (3.86), перейдемо від проміжків до нечітких множин ¹⁾.

Нижче цей метод ілюструється на прикладі узагальнення на нечіткі множини типу 2 поняття перерізу, яке визначено вище (див.(3.35)) для нечітких множин типу 1.

Вихідною точкою є вираз для функції належності перетину А та В, де А та В — нечіткі підмножини типу 1 множини U,

.

Якщо та — проміжки в , а не точки в , тобто якщо для фіксованого и

¹⁾ Ми припускаємо, що розглядувані нечіткі множини випуклі і, відповідно їх множинами рівня є інтервали [9]. У випадку не випуклих множин потрібні тільки незначні зміни в цій процедурі.

,

,

де а₁, а­­₂, b₁, b₂ залежать від и, то застосувавши принцип узагальнення (3.86) до функції (min), отримуємо ¹⁾

. (3.100)

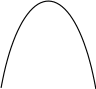
Рисунок 3.5 Переріз нечітких множин, значеннями функцій належності яких є проміжки

¹⁾ Рівність (3.100) можна отримати, використовуючи принцип узагальнення і в формі (3.90), якщо розглядати функцію (min) як відображення .

Таким чином, якщо значення функцій належності підмножин А та В — проміжки в , як показано на рисунку 3.5, то переріз цих множин описується функцією належності, значення якої (відрізки) для кожного и задаються формулою (3.100).

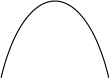
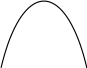
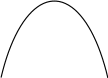
Рисунок 3.6 Множини рівня нечітких функцій належності µ_А та µ_В

Розглянемо тепер випадок, коли для кожного и множини та — нечіткі підмножини проміжку . Для простоти припустимо, що ці підмножини випуклі, тобто множини рівня — проміжки. Іншими словами, припускатимемо, що для кожного множини рівня нечітких підмножин А та В описуються функціями належності , значеннями яких є проміжки (див. рисунок 3.6) ¹⁾.

¹⁾ точне означення функцій та наведено нижче (див.(3.101) та (3.102))

Застосовуючи принцип узагальнення в формі (3.86) до множин рівня нечітких підмножин А та В, прийдемо до наступного означення перерізу нечітких множин типу 2.

Означення 3.2 Нехай А та В — нечіткі підмножини типу 2 множини U, такі, що для кожного множини та — випуклі нечіткі підмножини типу 1 проміжку , тобто для кожного множини рівня нечітких функцій належності та описуються функціями належності та , значеннями яких є проміжки.

Позначимо множину рівня нечіткої функції належності перерізу А та В через , причому множини рівня та визначаються для кожного и наступним чином

(3.101)

, (3.102)

де означає ступінь належності точки нечіткій множині ( ). Тоді для кожного и маємо

. (3.103)

Іншими словами, множина рівня нечіткої функції належності перерізу А та В є мінімум (в розумінні означення (3.100)) множин рівня нечіткої функції належності підмножин А та В. Використовуючи розклад (3.28), можна виразити у вигляді

. (3.104)

Розглянемо випадок, коли носії нечітких множин , — скінченні множини, тобто та можна представити у вигляді

, (3.105)

. (3.106)

Тут та — ступені належності та множинам та відповідно. Застосовуючи принцип узагальнення в формі (3.96) до операції (min), отримаємо потрібний вираз для ¹⁾.

(3.107)

Приклад 3.13 Проілюструємо рівність (3.104), припустивши, що в точці и ступені належності и множинам А та В позначаються як високий та середній відповідно, причому терміни високий та середній визначаються як нечіткі підмножини множини виразами

, (3.108)

. (3.109)

Множини рівня нечітких підмножин високий та середній виражаються наступним чином

,

¹⁾ Цей вираз можна вивести також із (3.90)

,

,

,

,

отже, множини рівня перерізу А та В мають вигляд

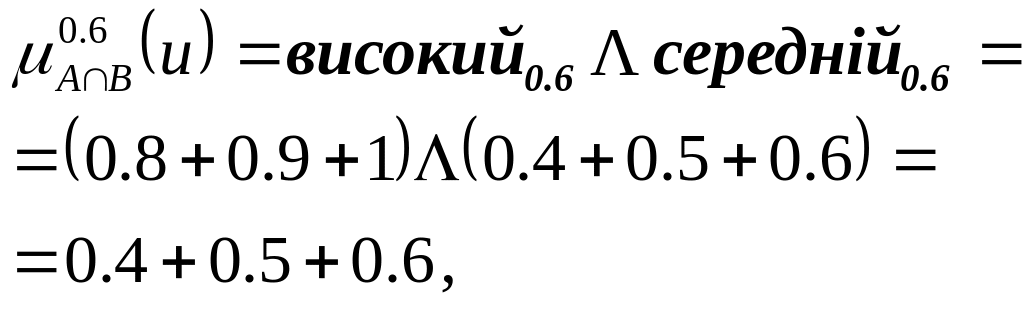(3.110)

(3.111)

(3.112)

Комбінуючи (3.110), (3.111) та (3.112), отримуємо вираз для нечіткої множини, яка описує ступінь належності точки и перерізу підмножин А та В

(3.113)

що еквівалентно твердженню

. (3.114)

Цей самий результат можна отримати коротшим способом, використовуючи рівність (3.107)

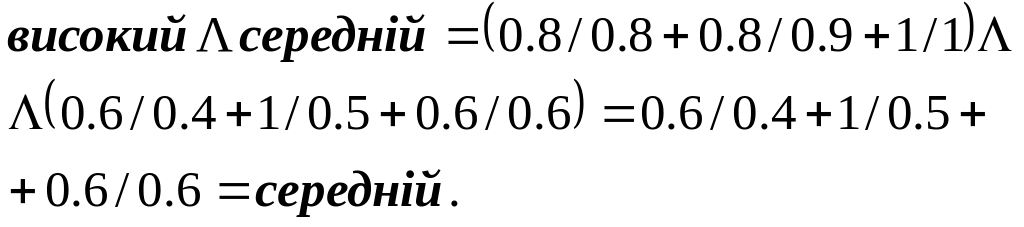(3.115)

Аналогічно можна узагальнити на випадок нечітких множин типу 2 операції доповнення, об’єднання, концентрування і т.д. Це проведено в §6 при обговоренні нечіткої логіки, в якій значення істинності є лінгвістичним за своєю природою.

Зауваження 3.7 Результати, отримані в прикладі 3.13, можна розглядати як частковий випадок загального висновку, який можна отримати із (3.100), про узагальнення нерівності на випадок нечітких підмножин числової осі. Зокрема, у випадку дійсних чисел а та b маємо

. (3.116)

На основі цієї еквівалентності, враховуючи вираз (3.100), отримуємо для проміжків

та . (3.117)

Звідси, в свою чергу, випливає

Означення 3.3 Нехай А та В — випуклі нечіткі підмножини числової осі, і нехай та — множини рівня цих підмножин відповідно. Тоді узагальнення нерівності на випуклі нечіткі підмножини дійсних чисел виражається ¹⁾ у вигляді

(3.118)

для всіх , (3.119)

де множина виражається згідно (3.100).

У випадку, розглянутому в прикладі 3.13, легко перевірити, що

для всіх (3.120)

¹⁾ Легко перевірити, що відношення , визначене в (3.117), є частково впорядкованим.

в розумінні (3.119), звідки ми приходимо до виразу

,

який цілковито узгоджується з (3.114).

67