►Докажем это утверждение для двух операций: для тензорного произведения и свертывания (для остальных оно практически очевидно).
Для
упрощения записи возьмем тензоры
типа (2, 1) и
типа (1, 1). Объект
в каждом базисе линейного пространства
задается совокупностью
компонент
.
Остается показать, что эти компоненты
при переходе от одного базиса к другому
меняются по тензорному закону.
Пусть в линейном пространстве наряду с базисом (8.4) задан ещё один базис
(8.5)
и пусть – матрица перехода от (8.4) к (8.5), – обратная к ней. Записываем последовательную цепочку преобразований:
=
[
и
– тензоры] =
=
=
=
.
Таким образом, для тензорного произведения теорема доказана.
При доказательстве теоремы для свертки используется равенство
,
(8.6)
доказанное
в § 9 гл. 3. Для упрощения записи опять же
возьмем тензор
типа (3, 2) и свернем его по второму верхнему
и второму нижнему индексам. В результате
получим объект
,
причем
=
[
– тензор] =
=
=
=[(8.6)]
=
= [суммирование по
]
=
=
.
Таким образом, теорема доказана и для свертывания.◄
Лемма
8.2. Пусть
– некоторый набор
чисел. Если для любого набора
чисел
при
всех значениях индексов
от 1 и до
,
то
опять же при всех значениях входящих
индексов от 1 и до
.
►Для упрощения записи доказательство проведем для однократного и двойного суммирований.
Однократное
суммирование.
Пусть
Положим
.
Тогда
.
Двойное
суммирование.
Пусть для любого набора чисел
и при всех
(8.7)
Положим
.
Тогда
.
Расшифруем
подробнее это доказательство при
.
Равенство (8.7) выглядит так:
.
Если
в (8.7) создается иллюзия, что на
можно сократить, то при подробной записи
видно, что этого сделать нельзя. Запишем
при некоторых значениях
и
:
;
;
.
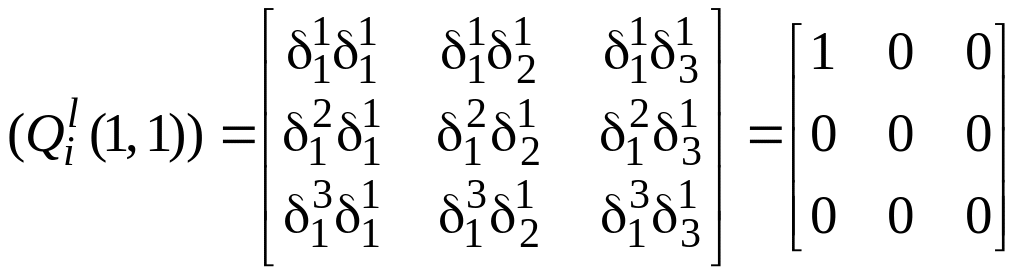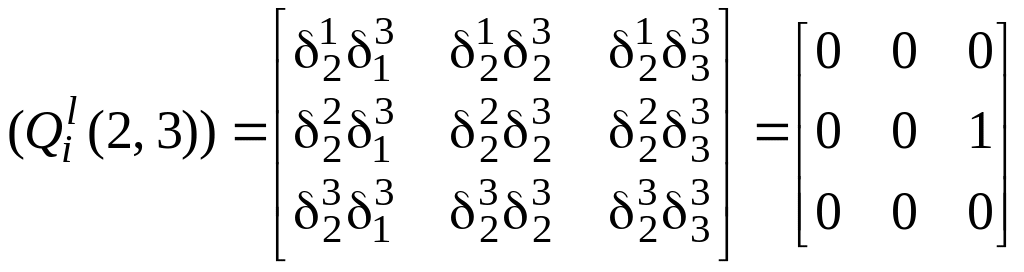Таким образом, видим,
что из девяти чисел
отличным от нуля будет только одно, что
и позволяет в сумме (8.7) вычленить одно
слагаемое. ◄
Теорема
8.2 (обратный тензорный признак).
Пусть
– объект, который в каждом базисе
линейного пространства
задается
совокупностью
чисел
.
Если в результате тензорного произведения
или взаимного свертывания объекта
с произвольным тензором заданного типа
получится тензор, то исходный объект
– тоже тензор.
►Для
упрощения записи доказательство проведем
для тензоров небольшой валентности.
Пусть
– неизвестный объект, и пусть для любого
тензора
типа (1, 1) тензорное произведение
=
является
тензором. Значит,
.
(8.8)
Так
как это равенство справедливо
,
положим
при всех значениях
и
.
Тогда из (8.8) вытекает, что
.
Таким образом, компоненты объекта Т
меняются по тензорному закону, поэтому
Т
и является тензором.
Теперь проведем доказательство для однократного взаимного свертывания.
Пусть
– неизвестный объект, и пусть для любого
тензора
типа (1, 0) результат взаимного свертывания
по нижнему индексу объекта Т
и верхнему индексу тензора
является тензором. Если
,
где
,
то
.
Из
этого равенства на основании леммы 8.2
мы и получаем, что
.
Аналогично утверждение доказывается
и для большего количества свёртываний.◄