§ 4. Ортогональные системы векторов

Определения. Векторы и евклидова пространства называются ортогональными или перпендикулярными, если их скалярное произведение равно 0.

Система векторов называется ортогональной, если ее векторы попарно ортогональны, т. е. если при

Ортогональная система называется ортонормированной, если все ее векторы имеют единичную длину.

Замечание. Несмотря на то, что понятие угла между векторами в комплексном евклидовом пространстве не вводится, ортогональность векторов определяется как в действительном евклидовом пространстве, так и в комплексном.

На основании следствий из аксиом § 1, нулевой вектор ортогонален всем векторам евклидова пространства. Верно и обратное утверждение.

Лемма 6.1. Если вектор ортогонален всем векторам пространства , то он нулевой.

► Пусть Положим Тогда , откуда и вытекает, что .◄

Теорема 6.3. Ортогональная система ненулевых векторов евклидова пространства линейно независима.

►Пусть задана ортогональная система

(6.4)

ненулевых векторов. Для доказательства линейной независимости, как обычно, составляем линейную комбинацию этой системы и приравниваем ее :

. (6.5)

Умножим скалярно (6.5) справа на , . Получаем

. (6.6)

Система (6.4) ортогональна, поэтому в левой части (6.6) остается только одно слагаемое, т. е. (6.6) принимает вид . Так как все векторы системы ненулевые, это равенство можно разделить на , откуда и получаем, что . Таким образом, система (6.5) линейно независима◄.

§ 5. Процесс ортогонализации Шмидта

Теорема 6.4. В любом конечномерном евклидовом пространстве существует ортонормированный базис.

►Выберем в какой-либо базис

(6.7)

и на его основе построим систему векторов:

(6.8)

При любом и при любом наборе вектор , так как он представляет собой линейную комбинацию линейно независимых векторов , причем коэффициент при отличен от нуля (равен 1).

Подберем коэффициенты так, чтобы любой из векторов был ортогонален всем предыдущим. Для этого -е равенство из (6.8) умножим скалярно справа на . Например, при = 2 получаем

,

откуда следует, что . При остальных умножениях уже учтем, что при .

.

После конечного числа шагов получаем ортогональную систему ненулевых векторов , которая по теореме 6.3 линейно независима, а значит, в -мерном евклидовом пространстве является базисом. Для того чтобы получить ортонормированный базис, векторы осталось только пронормировать, т. е. каждый разделить на его длину.◄

Процесс доказательства теоремы 6.4 и называется процессом ортогонализации Шмидта.

Пример. В пространстве многочленов степени не выше двух, в котором скалярное произведение задается формулой

,

построим ортонормированный базис, исходя из базиса

.

▼Поступаем точно так же, как и при доказательстве теоремы. Положим и подберем числа так, чтобы функции были ортогональными.

.

Таким образом, получили ортогональный базис

.

Теперь эти векторы остается пронормировать.

.

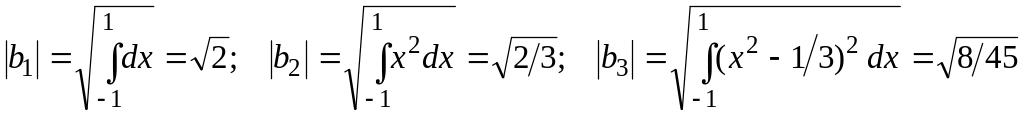Итак, ортонормированный базис:

.▲