Тема 9. Основы теории массообмеНа

Под массообменом понимают самопроизвольный необратимый процесс переноса массы определенного компонента в пространстве с неоднородным полем химического потенциала этого компонента. В простейшем случае неоднородным является поле концентрацией или парциального давления, приэтом процесс массообмена имеет определенную направленность. Например, в смеси с одинаковой температурой и давлением процесс массопереноса (диффузии) направлен к выравниванию концентраций в системе. При этом происходит перенос вещества из области с большей концентрацией. Диффузия – это перенос вещества молекулярным или молярным путем. Молекулярная диффузия – это перенос вещества в смеси, обусловленный тепловым движением микрочастиц. Молярный перенос неразрывно связан с макродвижением самой смеси, т.е. конвекцией. Массообмен, обусловленный совместным действием молярной диффузии и конвективного переноса вещества, называется конвективным массообменом. Потоком массы называется количество вещества, проходящего в единицу времени через данную поверхность в направлении нормали к ней. Он обозначается через I и измеряется в кг/с. Плотность потока массы j – это поток массы, проходящий через единицу поверхности: j=dI/dF.

Причиной возникновения потока массы являются:

- неравномерное распределение концентрации вещества, называемое

концентрационной диффузией;

- неоднородное температурное поле обуславливает термодиффузию;

- неоднородное поле давления определяет возникновение бародиффзузии.

Если в двухкомпонентной смеси отсутствует макродвижение, а температура и давление остаются постоянными по всему объему системы, то плотность потока массы одного из компонентов, обусловленного молекулярной диффузией, определяется законом Фика: , (9.1)

где D – коэффициент диффузии, м² /с; с_i – местная концентрация данного компонента, равная отношению массы компонента к объему смеси, кг/м³ ; - градиент концентрации (вектор), кг/м⁴ .

В рассматриваемом случае движущей силой является градиент концентрации. Знак „ -” в выражении обусловлен тем, что плотность потока массы направлена в сторону убывания концентрации, а градиент концентрации – в противоположную сторону.

Закон Фика описывает концентрационную диффузию, в результате

которой переносится основная доля вещества. Перенос вещества осуществляется также под действием градиента температур. Такой перенос вещества называется термодиффузией (эффект Соре). Молекулы компоненты с большей массой стремятся перейти в область низких температур. При одинаковых массах молекул, то в холодную область стремятся перейти более крупные молекулы. В результате термодиффузии возникает градиент концентрации.

Градиент концентрации является движущей силой концентрационной диффузии, величина его определяет интенсивность этого процесса. Из кинетической теории газов известно (и опыты это подтверждают), что величина D возрастает с увеличением температуры и уменьшается с ростом давления газа. Ее значение зависит и от соотношения компонентов, но зависимость эта слабая, ее учитывают очень редко. Вообще же коэффициент D относится к классу физконстант, значения его определяют экспериментально и приводят в соответствующих справочниках.

Массовая концентрация представляет собой собственно говоря плотность данного компонента. Считая, что компоненты смеси находятся в идеальногазовом состоянии и для каждого из них применимо уравнение состояния , формулу (9.1) можно записать через градиент парциального давления.

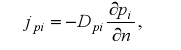
где D_pi – коэффициент молекулярной диффузии, отнесенный к градиенту авления. Ясно, что D_pi = Di/RiT и Di = Di/R1T = Di/R2T = D, откуда видно, что коэффициент диффузии одинаков для обоих компонент смеси.

Если смесь неоднородна и температура ее различна в различных ее точках, то возникает термодиффузия: более тяжелые и крупные молекулы одного из компонентов стремятся перейти в холодные области, легкие и мелкие другого – в теплые (это называют эффектом Соре). Если в смеси имеются области с разным давлением, то происходит бародиффузия, когда компонент с тяжелыми молекулами устремляется в область повышенного давления, а другой компонент – в область пониженного давления. Механизмом этих явлений вскрывает молекулярно-кинетическая теория, но мы не будем в нее углубляться, ибо это предмет общефизической теории. В общем случае, при наличии всех трех видов диффузии, термо- и бародиффузии создают определенный градиент концентраци, что вызывает противоположно направленный концентрационный массоперенос. Так что с течением времени возможно установление концентрационного равновесия и при наличии градиентов температуры и давления. При этом плотность потока массы определяют с учетом всех составляющих процесса

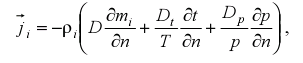
где D_t = k_tD, D_p = k_pD – коэффициенты термо- и бародиффузии; k_t и k_p – термодиффузионное и бародиффузионное отношения.

При конвективном массопереносе поток массы определяется скоростью w и плотностью компонента

Суммарный поток вещества в результате молекулярного и конвективного переносов будет

Вместе с массой переносится и энтальпия компонента

где h_i – удельная энтальпия. Значит при наличии массообмена плотность теплового потока будет описываться следующим уравнением:

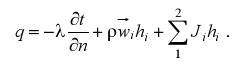(9.2)

Здесь первое слагаемое учитывает перенос тепла теплопроводностью, второе – конвекцией, а третье – молекулярной диффузией.