
- •Задания и общие рекомендации
- •1. Формирование исходных эмпирических данных.
- •Содержание контрольной работы.
- •Пример, поясняющий основные этапы статистического исследования
- •Арифметическая средневзвешенная вариационного ряда:
- •Структурные средние величины вариационного ряда
- •Показатели вариации и оценка степени однородности
- •Оценка тесноты линейной связи между признаками исследуемой совокупности
- •Вопросы итогового контроля
Арифметическая средневзвешенная вариационного ряда:
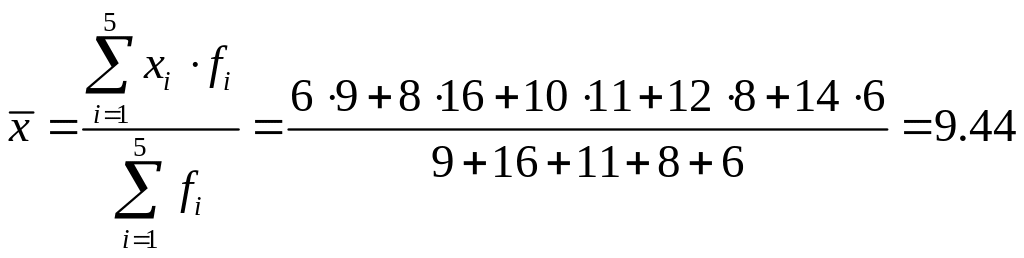 млн. руб.
млн. руб.
Структурные средние величины вариационного ряда
1. Мода вариационного ряда:
![]() ;
;
где:
![]() - нижняя граница модального интервала;
- нижняя граница модального интервала;
![]() - величина модального интервала;
- величина модального интервала;
![]() - частота модального интервала;
- частота модального интервала;
![]() - частота предмодального (предшествующего)
интервала;
- частота предмодального (предшествующего)
интервала;
![]() - частота постмодального (последующего)
интервала.
- частота постмодального (последующего)
интервала.
![]() млн. руб.
млн. руб.
2. Квартили вариационного ряда:
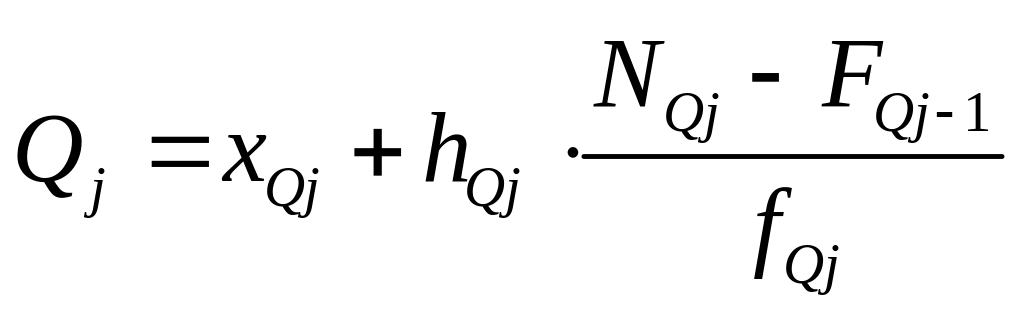 ;
;
где:
![]() - индекс соответствующего квартиля;
- индекс соответствующего квартиля;
![]() - нижняя граница интервала, в котором
находится квартиль.
- нижняя граница интервала, в котором
находится квартиль.
![]() - величина интервала, в котором находится
квартиль;
- величина интервала, в котором находится
квартиль;
![]() - порядковый номер квартиля;
- порядковый номер квартиля;
![]() - частота интервала, в котором находится
квартиль;
- частота интервала, в котором находится
квартиль;
![]() - накопленная частота интервала, который
предшествует интервалу, содержащему
квартиль.
- накопленная частота интервала, который
предшествует интервалу, содержащему
квартиль.
![]() .
Первый квартиль находится в интервале
7-9.
.
Первый квартиль находится в интервале
7-9.
Значение первого квартиля:
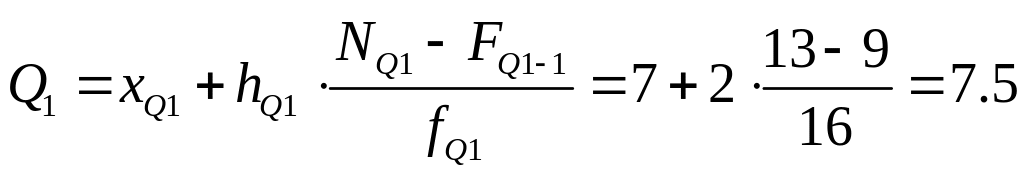 млн. руб.
млн. руб.
![]() .
Первый квартиль находится также в
интервале 7-9. Однако значение второго
квартиля (медианы), конечно, отличается
от первого:
.
Первый квартиль находится также в
интервале 7-9. Однако значение второго
квартиля (медианы), конечно, отличается
от первого:
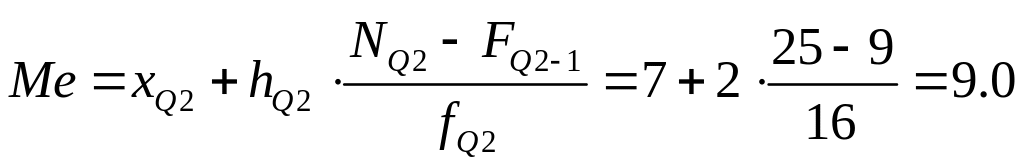 млн. руб.
млн. руб.
![]() .
Третий квартиль находится в интервале
11-13. Его значение:
.
Третий квартиль находится в интервале
11-13. Его значение:
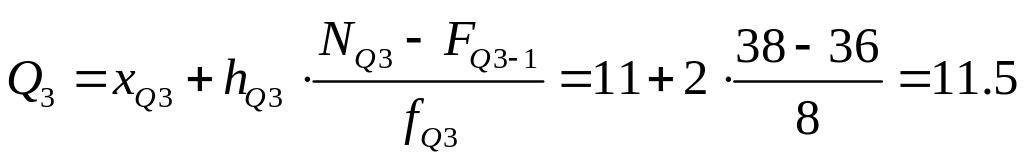 млн. руб.
млн. руб.
Выводы по структуре вариационного ряда.
А) Используем моду и медиану. У наибольшего числа предприятий стоимость основных фондов составляет 8.2 млн. руб. У половины предприятий стоимость основных фондов составляет менее 9 млн. руб., а у другой половины – более 9 млн. руб.
Б) Используем квартили. Квартили как отдельные значения группировочного признака делят исследуемые предприятия на 4 равновеликие части. Стоимость основных фондов у 25 % предприятий не превышает 7.5 млн. руб., еще у 25% предприятий стоимость основных фондов составляет не менее 11.5 млн. руб., а у оставшихся 50 % предприятий стоимость основных фондов составляет от 7.5 до 11.5 млн. руб.
Поскольку выполняется неравенство
![]() ,
то имеет место незначительная
правосторонняя асимметрия. Вместе с
тем возможны практические ситуации,
когда в первом приближении можно приять
симметричный характер вариационного
ряда, т.е.
,
то имеет место незначительная
правосторонняя асимметрия. Вместе с
тем возможны практические ситуации,
когда в первом приближении можно приять
симметричный характер вариационного
ряда, т.е.
![]() .
.
Показатели вариации и оценка степени однородности
1. Дисперсия
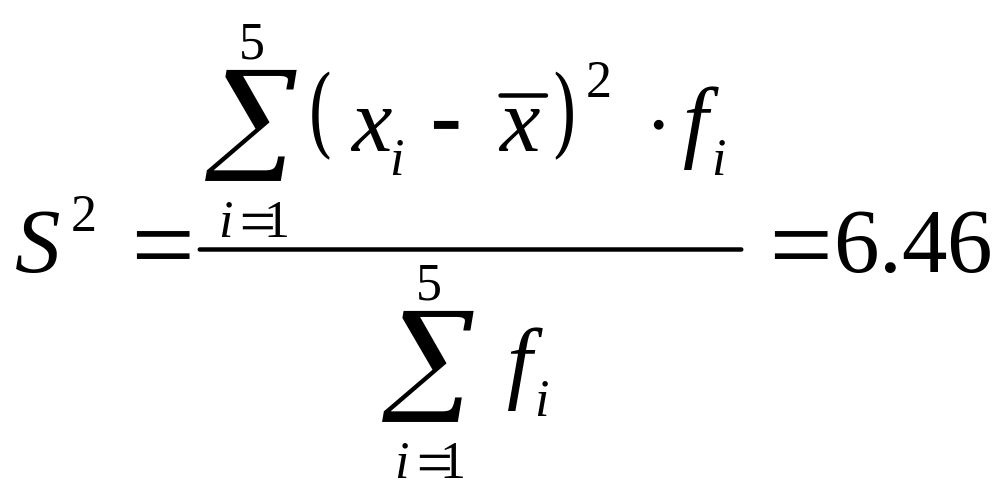
2. Среднеквадратичное отклонение
![]() млн. руб.
млн. руб.
3. Коэффициент вариации
![]() .
.
Вывод об однородности, исследуемой совокупности.
Эмпирический коэффициент вариации
![]() ,
следовательно, исследуемую статистическую
совокупность еще можно считать однородной.
,
следовательно, исследуемую статистическую
совокупность еще можно считать однородной.
Оценка тесноты линейной связи между признаками исследуемой совокупности
Коэффициент парной корреляции
рассчитывается по исходным статистическим
данным, т.е. с использованием всех
![]() пар эмпирических точек
.
Так и необходимо поступать при
выполнении контрольной работы! В
данном лекционном примере требуемых
исходных данных нет, поэтому оценим
коэффициент парной корреляции
ориентировочно по средне групповым
значениям
пар эмпирических точек
.
Так и необходимо поступать при
выполнении контрольной работы! В
данном лекционном примере требуемых
исходных данных нет, поэтому оценим
коэффициент парной корреляции
ориентировочно по средне групповым
значениям
![]() где:
где:
![]() .
.
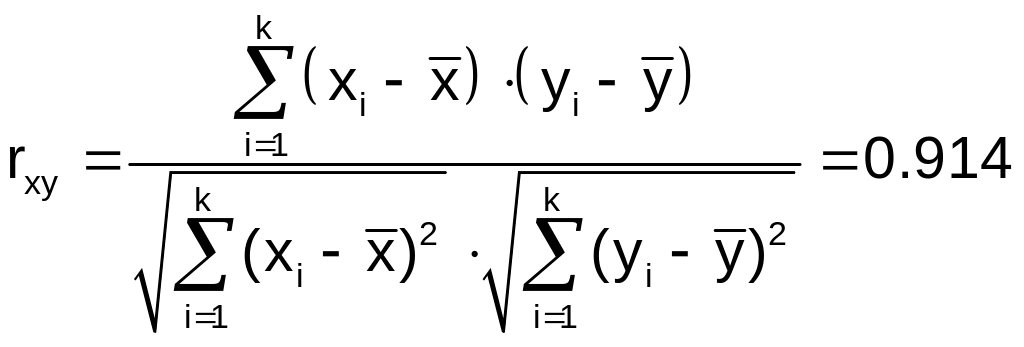 .
.
Где:
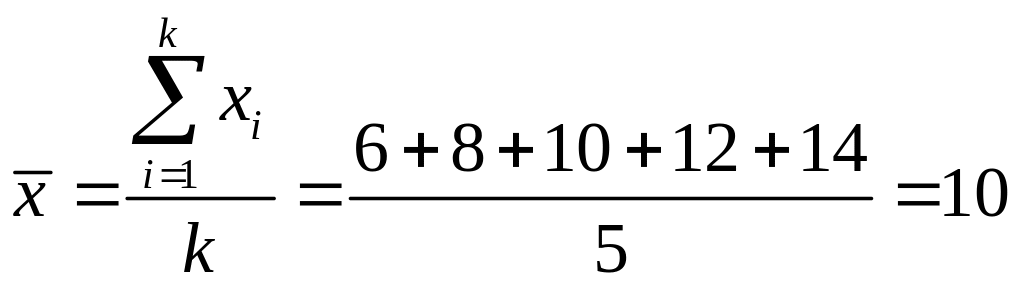 млн. руб.
млн. руб.
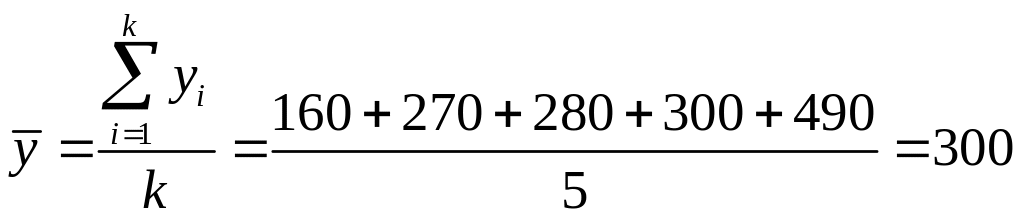 млн. руб.
млн. руб.
Поскольку
![]() то линейная связь между параметрами
тесная.
то линейная связь между параметрами
тесная.
Оценка значимости коэффициента корреляции
Вывод о статистической значимости коэффициента парной корреляции делается на основе сравнения его теоретической и экспериментальной модели (на основе сравнения теоретического и экспериментального критерия Стьюдента).
Экспериментальный критерий Стьюдента:
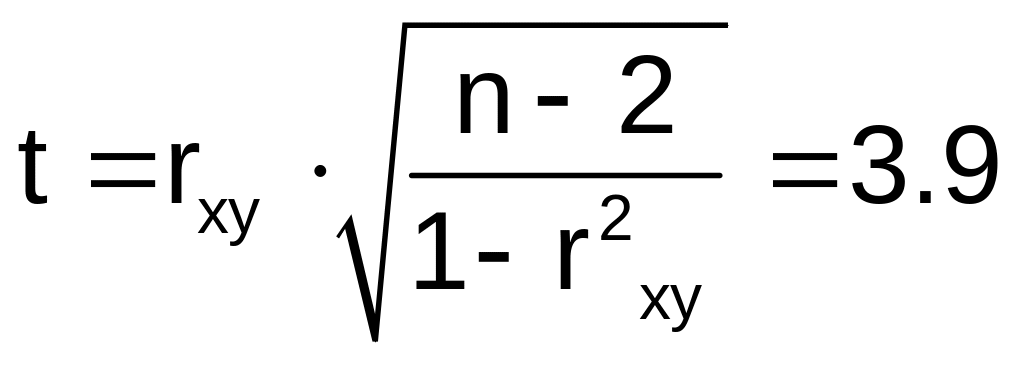
Теоретический (табличный) критерий
Стьюдента при доверительной вероятности
![]() и степени свободы
и степени свободы
![]() :
:
![]() .
.
Поскольку выполняется условие
![]() ,
то можно считать коэффициент парной
корреляции статистически значимым.
,
то можно считать коэффициент парной
корреляции статистически значимым.
Разработка линейной регрессионной модели.
Разработка уравнения линейной регрессии
производится с использованием исходным
статистическим данным, т.е. с использованием
всех
пар эмпирических точек
.
Так и необходимо поступать при
выполнении контрольной работы! В
данном лекционном примере требуемых
исходных данных нет, поэтому приведем
общий алгоритм разработки уравнения
регрессии
![]() на примере средне групповых значений
признаков
где:
.
на примере средне групповых значений
признаков
где:
.
Параметры уравнения регрессии можно рассчитать по известным формулам:
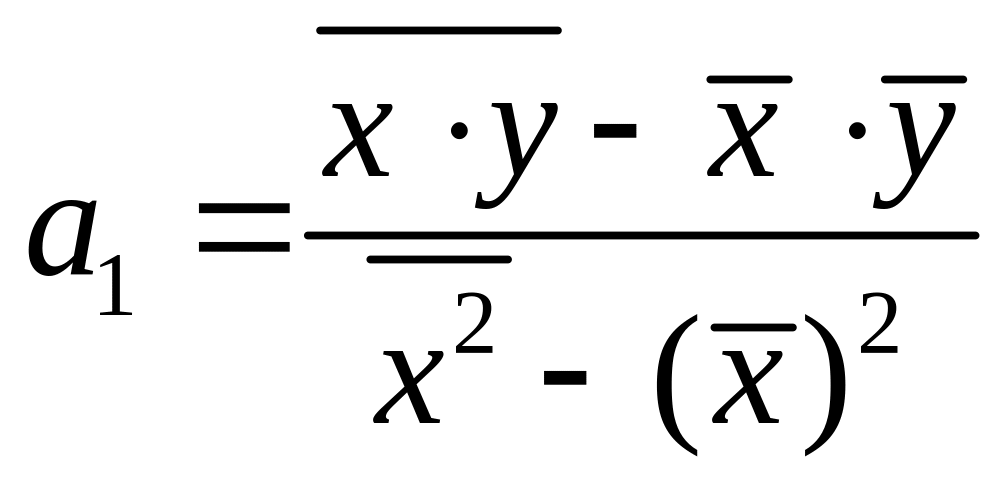 либо
либо
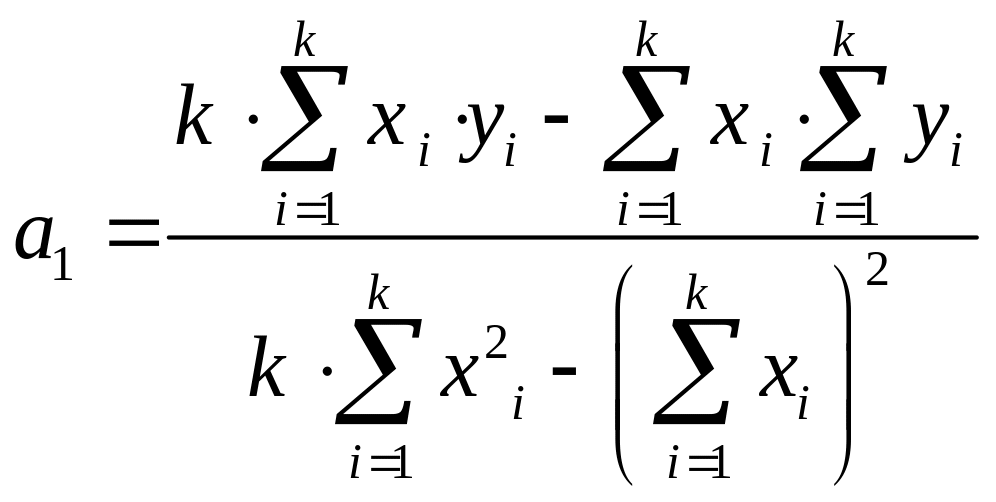 ;
;
![]() .
.
![]() ;
;
![]()
Окончательно линейная модель для рассматриваемого примера:
![]() млн. руб.
млн. руб.
Числовые векторы расчетных и табличных значений:
![]() ;
;
![]() .
Необходимо количественно оценить
расхождение невязку полученных расчетных
и табличных (эмпирических) значений.
Для этого можно использовать ошибку
прогнозирования:
.
Необходимо количественно оценить
расхождение невязку полученных расчетных
и табличных (эмпирических) значений.
Для этого можно использовать ошибку
прогнозирования:
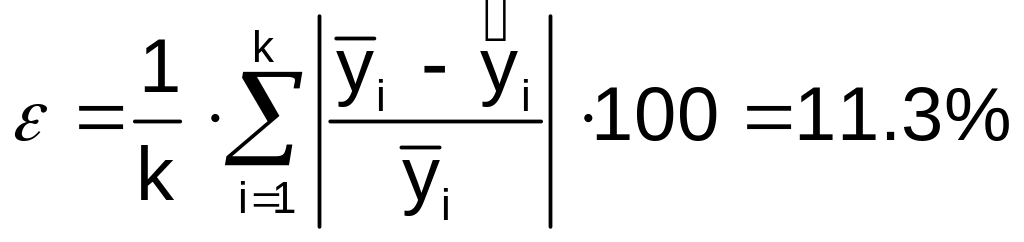 .
.
Необходимо сделать соответствующий вывод.
Задания и рекомендации разработал, доцент: А.С. Андреев
28.03.2012 г
