Кручение. Условие прочности и жескости при кручении.
Кручением называется такой вид деформации, при котором в поперечном сечении вала возникает только крутящий момент Мкр, а все остальные внутренние силовые факторы равны нулю.
Уравнение равновесия:
Деформация - угол сдвига
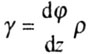
Напряжения
-
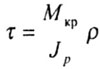
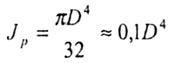полярный момент инерции;
D - диаметр стержня круглого поперечного сечения,
-
касательные напряжения, р • расстояние
от точки, где определяется до центра
вала.
Угол закручивания элемента
-
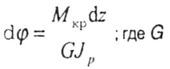модуль упругости второго рода
Угол закручивания стержня
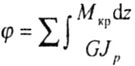
При кручении расчеты на прочность также делятся на проектировочные и поверочные. В основе расчетов лежит условие прочности
где τmax - максимальное касательное напряжение в брусе, определяемое по вышеприведенным уравнениям в зависимости от формы сечения; [τ] - допускаемое касательное напряжение, равное части предельного напряжения для материала детали - предела прочности τв или предела текучести τт. Коэффициент запаса прочности устанавливается из тех же соображений, что и при растяжении. Например, для вала полого круглого поперечного сечения, с внешним диаметром D и внутренним диаметром d, имеем
,
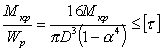где α=d/D - коэффициент полости сечения.
Условие жесткости такого вала при кручении имеет следующий вид:
,
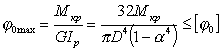где [φo] - допускаемый относительный угол закручивания.
Билет 3
Напряжённое состояние в точке. Определение напряжений в наклонной площадке для общего случая напряжённого состояния.
Схемы напряженного состояния графически отображают наличие и направление главных напряжений в рассматриваемой точке тела. Напряжения в точке изображаются как напряжения на трех бесконечно малых гранях куба, соответственно перпендикулярных главным осям. Возможны девять схем напряженного состояния (рисунок, позиция а). Напряженное состояние в точке может быть линейным, плоским или объемным.
Схемы с напряжениями одного знака называют одноименными, а с напряжениями разных знаков – разноименными. Условно растягивающие напряжения считают положительными, с сжимающие – отрицательными.
Схема напряженного состояния оказывает влияние на пластичность металла. На значение главных напряжений оказывают существенное влияние силы трения, возникающие в месте контакта заготовки с инструментом, и форма инструмента. В условиях всестороннего неравномерного сжатия при прессовании, ковке, штамповке сжимающие напряжения препятствуют нарушению межкристаллических связей, способствуют развитию внутрикристаллических сдвигов, что благоприятно сказывается на процессах обработки металлов давлением (см. все записи с тегом ОМД). В реальных процессах обработки давлением в большинстве случаев встречаются схемы всестороннего сжатия и состояния с одним растягивающим и двумя сжимающими напряжениями.
Напряженным состоянием тела в точке называют совокупность нормальных и касательных напряжений, действующих по всем площадкам (сечениям), содержащим данную точку.
Исследование напряженного состояния дает возможность анализировать прочность материала для любого случая нагружения тела.
Пусть в окрестности исследуемой точки шестью попарно параллельными плоскостями выделен элементарный прямоугольный параллелепипед с размерами ребер dx, dy и dz. По его граням будут действовать нормальные “si” и касательные “tij” напряжения.
Обозначения нормальных напряжений содержат один индекс - наименование оси, которой параллельно данное напряжение. В обозначении касательных напряжений используются два индекса: первый совпадает с индексом нормального напряжения, действующего по данной площадке, а второй - наименование оси, которой параллельно данное касательное напряжение.
Используем принятое правило знаков для напряжений. Нормальное напряжение σ считается положительным, если совпадает по направлению с внешней нормалью к площадке, касательные напряжения t считаются положительными, если вектор касательных напряжений следует поворачивать против хода часовой стрелки до совпадения с внешней нормалью. Отрицательными считаются напряжения обратных направлений .