Чистый сдвиг. Деформация при сдвиге. Закон Гука при сдвиге.
Чистый сдвиг — это такое напряженное состояние, когда на гранях выделенного из бруса элемента действуют только касательные напряжения. Такие грани называются площадками чистого сдвига.
Величина a - абсолютный сдвиг, γ = tg γ = a/h - относительный сдвиг.
С деформацией сдвига мы встречаемся при резании ножницами металла, при работе различных соединений (резьбовых, шлицевых, шпоночныхб заклёпочных и сварных содениениях).
При сдвиге деформация создается двумя равными и противоположно направленными внешними силами Р, действующими в плоскости поперечного сечения тела на весьма малом расстоянии ∆ вдоль оси. Такая деформация вызывает сдвиг поперечных сечений, который при дальнейшем увеличении внешней нагрузки завершается разрушением тела в виде среза.
Срез широко используется в технологии машиностроения — чтобы получить заготовки при разрезании проката пластичных металлов на прессах, механических ножницах и в вырубных штампах.
Деформации сдвига подвергаются многие детали: шпонки, штифты, заклепки, болты и др.
Пользуясь методом сечений, можно записать условие прочности тела, которое подвергается деформации сдвига:
τ = Р / F ≤ [τ]сд,
где τ — действительные напряжения при сдвиге;
[τ]сд — допустимое напряжение при сдвиге.
Из этой формулы можно определить прочностную величину площади поперечного сечения детали при сдвиге
F = Р / [τ]сд.
По аналогии с растяжением – сжатием, закон Гука при сдвиге в абсолютных координатах имеет следующий вид:
, (5.2)
где G - модуль сдвига или модуль упругости второго рода. Можно показать, что модуль сдвига связан с модулем упругости первого рода и коэффициентом Пуассона следующим, хорошо согласующимся с опытом, уравнением:
. (5.3)
Для стали модуль сдвига G=8·104 МПа.
Из уравнения (5.2) с учетом (5.1) может быть получен закон Гука при сдвиге в относительных координатах:
(5.4)
или
. (5.5)
Закон Гука справедлив лишь до предела пропорциональности. При испытаниях на сдвиг образцов из пластичных материалов так же, как и при растяжении, наблюдается явление текучести. Предел текучести обозначается через τт, а предел прочности – через τв.
Билет 2.
Диаграммы растяжения и сжатия для пластичных и хрупких материалов. Их характерные точки. Характеристики прочности и пластичности.
Диаграмма
характеризует свойства испытуемого
материала и называется условной
диаграммой растяжения, так как напряжения
и относительные удлинения вычислены
по отношению к первоначальной площади
сечения А0 и первоначальной длине .
Диаграмма растяжения образца из малоуглеродистой стали Ст3 характеризуется четырьмя участками.
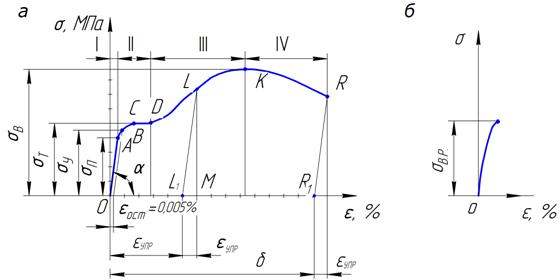
Участок
I соответствует упругим деформациям
материала, подчиняющимся закону Гука:
величина относительной деформации
прямо пропорциональна напряжению.
Отношение растягивающего усилия в точке
А к первоначальной площади поперечного
сечения называется пределом
пропорциональности:
Участок
II начинается после точки А, когда
диаграмма становится криволинейной.
Однако до точки В деформации остаются
упругими (восстанавливаются после
снятия нагрузки). Отношение растягивающего
усилия в точке В к площади А0 называется
пределом упругости:
– это такое напряжение, при котором
величина остаточной деформации не
превышает 0,005 %. При дальнейшем увеличении
нагрузки появляются неупругие (остаточные)
деформации. В точке С начинается процесс
деформирования образца без увеличения
внешней нагрузки. Это явление называется
текучестью материала, а участок CD –
площадкой текучести. Максимальное
напряжение, при котором происходит рост
деформации без увеличения силы, называется
пределом текучести:
. В зоне текучести у стальных образцов
существенно меняется электропроводность
и магнитные свойства. Поверхность
полированного образца покрывается
линиями (линии Чернова), наклоненными
к его оси, и становится матовой.
Для ряда материалов (медь, алюминий), не имеющих на диаграмме выраженной площадки текучести, вводят понятие условного предела текучести , под которым подразумевают напряжение, вызывающее остаточную деформацию, равную 0,2 %.
Участок III характеризуется увеличением нагрузки, при которой происходит дальнейшая деформация образца. Если образец нагрузить до состояния, соответствующего точке L диаграммы, а затем разгрузить, то процесс разгрузки на диаграмме будет обозначен прямой линией LL1, параллельной участку ОА. При разгрузке деформация полностью не исчезает: она уменьшается на величину L1М упругой части удлинения. Отрезок ОL1 представляет собой остаточную деформацию. Если образцу дать «отдохнуть» и подвергнуть повторному нагружению, то процесс пойдет по линии L1LKR. При этом предел пропорциональности значительно увеличится (точка L находится выше точки А), но при этом уменьшится пластичность. Это явление получило название наклепа.
Отношение
наибольшей нагрузки к первоначальной
площади поперечного сечения стержня
называется пределом временного
сопротивления:
. Пределу прочности соответствует
максимальное напряжение в образце до
его разрушения.
Участок IV начинается в точке К и заканчивается разрушением образца в точке R. Этот участок носит название зоны разрушения. Деформация образца на этом участке характерна образованием «шейки» и образовавшимся удлинением за счет его утонения. Площадь сечения образца в шейке быстро уменьшается и, как следствие, падает усилие и условное напряжение. Разрыв образца происходит по наименьшему сечению шейки.
Степень пластичности материала может быть охарактеризована величинами остаточного относительного удлинения образца, доведенного при растяжении до разрыва, и остаточного относительного сужения шейки:
Диаграмма
растяжения хрупких материалов (б)
характеризуется тем, что отклонение от
закона Гука начинается при малых
значениях деформирующей силы; диаграмма
не имеет площадки текучести; образцы
разрушаются при очень малой остаточной
деформации. За характеристику прочности
хрупких материалов принимают временное
сопротивление при растяжении
.
На
диаграмме растяжения (а) прямолинейный
участок ОА, соответствующий закону Гука
(
),
наклонен под углом к оси абсцисс:
Во избежание искривления металлические образцы, подлежащие испытанию на сжатие, выполняют в виде коротких цилиндров, высотой h≤3d, или кубиков. Образцы испытывают на специальных прессах.
Диаграмма сжатия образца из пластичного материала (а) совпадает в начальной стадии с диаграммой растяжения (линия OABCD). После точки D материал расплющивается и сжимающая сила быстро возрастает. Модуль упругости первого рода, а также пределы пропорциональности, упругости и текучести у малоуглеродистой стали при растяжении и сжатии можно считать совпадающими.
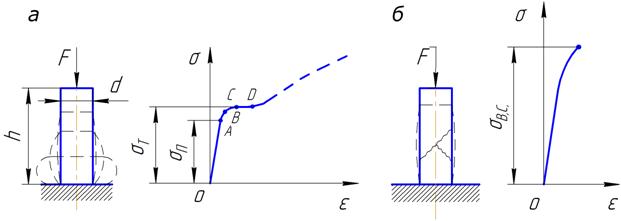
Разрушение хрупких образцов при сжатии, как и при растяжении, происходит при малой остаточной деформации (б). Разрушение образца происходит по площадкам возникновения максимальных касательных напряжений. Основной характеристикой хрупкого материала при сжатии является предел прочности , который оказывается выше, чем при растяжении, т.е. хрупкие материалы сопротивляются сжатию лучше, чем растяжению.
Характеристики прочности
1. Предел пропорциональности Опц = Fпц / Ao - наибольшее напряжение растяжения, при котором еще справедлив закон Гука. Здесь Fпц - нагрузка, определяемая по отклонению диаграммы (рис. 6, а) от первоначального прямолинейного участка.
2. Предел упругости Oу = Fy / Ao - представляет собой напряжение,
при котором остаточные деформации незначительны (0,001 - 0,003 %).
Практически можно считать предел упругости совпадающим с пределом пропорциональности.
3. Предел текучести От = Fт / Ao - напряжение, при котором наблюдается рост деформаций при постоянной нагрузке.
4. Предел прочности или временное сопротивление материалов Oв = Fmax / Ao - напряжение, вызванное наибольшей нагрузкой.
5. Истинное сопротивление разрыву Sk = Fk / Ak - напряжение, определяемое отношением нагрузки Fк в момент разрыва к площади поперечного сечения образца в месте разрыва.
Напряжения Oпц, От, Oпч являются уловными, т.к. они определяются по отношению к первоначальной площади поперечного сечения образца без учета уменьшения этой площади в процессе роста нагрузки.
Величины условных напряжений Опц, От практически не отличаются от истинных напряжений, отнесенных к фактической площади сечения.
На диаграмме показан закон разгрузки (линия НН1 параллельная ОА); при повторной нагрузке (после разгружения) диаграмма идет по линии Н1НДЕ. Явление повышения нагрузки, соответствующей пределу пропорциональности с одновременным уменьшением пластичности при повторном нагружении за пределом пропорциональности, называется наклепом.
Характеристики пластичности материала
δ - максимальное удлинение в момент разрыва
%,
где Δlmax – максимальное остаточное удлинение ;
ψ – максимальное сужение при разрыве
%,
где Аш – площадь образца в месте разрыва.
Характеристики пластичности определяют способность матер ала к деформированию, чем выше значения δ и ψ, тем матери пластичнее.
Ускорение характеризует не только изменение величины скорости, но и изменение ее направления. Очевидно, что быстрота изменения направления вектора скорости, при прочих равных условиях, зависит от степени искривленности траектории. Для количественной оценки этой искривленности вводится понятие кривизны.