4. Расчеты в условиях инфляции
Инфляция характеризуется обесцениванием национальной валюты и общим повышением уровня цен внутри страны. Измеряются темпы инфляции с помощью индексов цен, которые выражаются обычно в процентах и определяются по формуле:
(4.1.)
где
- количество товаров, включённых в
потребительскую корзину в анализируемом
периоде;
-
цены соответствующих товаров в
анализируемом периоде;
-
цены этих же товаров в базовом периоде.
Определенный уровень инфляции имеет свое название:
-
Индекс инфляции, %
Название инфляции
101
Низкая
110
Ползучая
200
Галопирующая
1100
Гиперинфляция
10100
Суперинфляция
В
долях единицы индекс инфляции
показывает, во сколько раз выросли цены
за рассматриваемый период.
Уровень
инфляции
(в %) показывает,
на сколько процентов выросли цены за
рассматриваемый период времени:
(4.2.)
где
- сумма, на которую надо увеличить
первоначальную сумму
для сохранения её покупательной
способности в будущем.
Взаимосвязь
между уровнем и индексом инфляции за
один и тот же период выражается формулой
(во всех формулах ниже, соответственно,
и
):
(4.3.)
(4.4.)
Индекс
инфляции за период, состоящий из
-го
количества более коротких периодов,
характеризующихся своим уровнем
инфляции, можно определить по формуле:
(4.5.)
где
- количество интервалов в наблюдаемом
периоде.
При равных интервалах и равных уровнях инфляции за каждый интервал формула принимает вид:
(4.6.)
Будущую сумму, покупательная способность которой с учётом инфляции будет равна покупательной способности первоначальной суммы , можно определить по формулам:
(4.7.)
Будущую
сумму
,
характеризующую реальное, обесцененное
в результате инфляции значение нынешней
суммы
,
можно определить по формуле:
(4.8.)
Следовательно, реальную покупательную способность наращенной суммы, обесцененной в результате действия инфляции можно определить следующим образом:
а) для ставки простых процентов:
(4.9.)
б) для ставки сложных процентов при их начислении один раз в конце года:
(4.10.)
в) при начислении сложных процентов несколько раз в году:
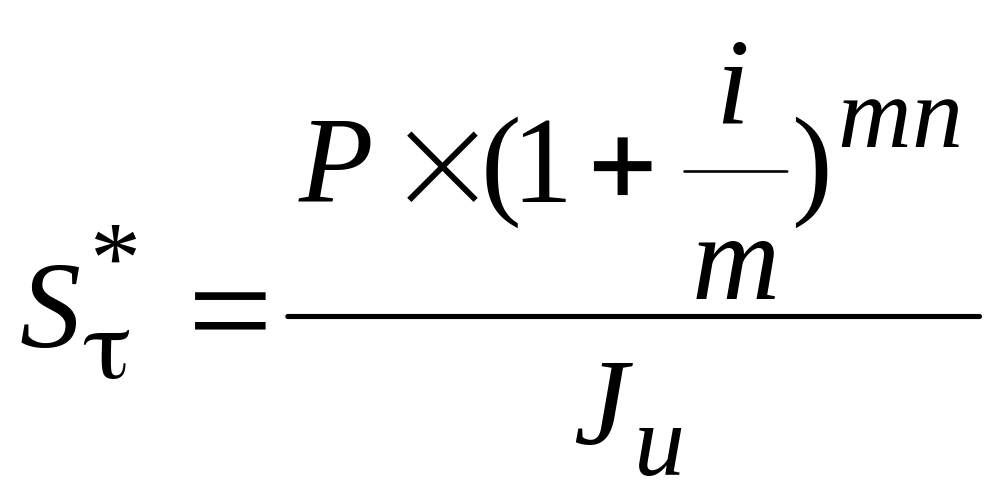(4.11.)
Компенсация потерь от инфляции осуществляется корректировкой процентной ставки:
Точная корректировка осуществляется по формуле:
(4.12.)
где
- ставка брутто – ставка, учитывающая
инфляцию;
- ставка процентов за период, характеризующая заданную, без учета действия инфляции доходность операции;
2. Приближённая корректировка:
(4.13.)
Вычисленное
значение ставки брутто
или
следует
подставлять в расчетные формулы вместо
ставки процентов
.
П Р А К Т И К У М
Задача 4.1. Определить ожидаемый годовой уровень инфляции при уровне инфляции за месяц при оптимистическом прогнозе 1,5% и пессимистическом прогнозе - 6% .
Задача 4.2. Определить уровень инфляции за 5 лет при уровне инфляции за месяц в размере 1,5%.
Задача 4.3. Вклад в сумме 50 тыс. руб. положен в банк на полгода. Начисление процентов производится ежемесячно по ставке 28% годовых. Определить реальный доход вкладчика для ожидаемого месячного уровня инфляции в 1% и 3%.
Задача 4.4. Сумма ссуды $10000. Выдана на 10 лет под 5% годовых. Еженедельный темп инфляции 2%. Определить сумму, которая застрахует кредитора от потерь, связанных с инфляционным обесцениванием денег.
Задача 4.5. Сумма ссуды $10000. Выдана на 10 лет под 5% годовых. Ежегодный темп инфляции 6%. Определить сумму, которая застрахует кредитора от потерь, связанных с инфляционным обесцениванием денег.
Задача 4.6. Определить срок, за который 100 тыс. руб превратятся в 100 руб, если годовой уровень инфляции составляет 8%.
Задача 4.7. Определить ожидаемый годовой уровень инфляции при котором 100 тыс. руб превратятся в 100 руб за 5 лет.
Задача 4.8. Студент 3 курса ИЭФ специальности «Экономика и управление на предприятии/ ж.д. строительство» собирается накопить1666 тыс. руб и приобрести автомобиль. Определить:
1. На какой срочный депозит следует внести первоначальный взнос, если банк начисляет сложные проценты с автоматическим возобновлением договора на следующих условиях:
-
Вид депозита
Номинальная ставка
годовых процентов, %
1 месяц
20
3 месяца
22
6 месяцев
24
1 год
26
2. Определить срок, за который он может накопить заданную сумму, если ежемесячный темп инфляции составляет 0,8%.